原文链接: https://leetcode-cn.com/problems/minimum-garden-perimeter-to-collect-enough-apples

英文原文

In a garden represented as an infinite 2D grid, there is an apple tree planted at every integer coordinate. The apple tree planted at an integer coordinate (i, j) has |i| + |j| apples growing on it.

You will buy an axis-aligned square plot of land that is centered at (0, 0).

Given an integer neededApples, return the minimum perimeter of a plot such that at least neededApples apples are inside or on the perimeter of that plot.

The value of |x| is defined as:

• x if x >= 0
• -x if x < 0

 

Example 1:

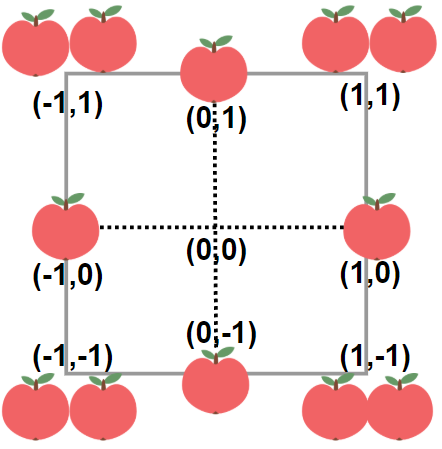
Input: neededApples = 1
Output: 8
Explanation: A square plot of side length 1 does not contain any apples.
However, a square plot of side length 2 has 12 apples inside (as depicted in the image above).
The perimeter is 2 * 4 = 8.

Example 2:

Input: neededApples = 13
Output: 16

Example 3:

Input: neededApples = 1000000000
Output: 5040

 

Constraints:

• 1 <= neededApples <= 1015

中文题目

给你一个用无限二维网格表示的花园，每一个 整数坐标处都有一棵苹果树。整数坐标 (i, j) 处的苹果树有 |i| + |j| 个苹果。

你将会买下正中心坐标是 (0, 0) 的一块 正方形土地 ，且每条边都与两条坐标轴之一平行。

给你一个整数 neededApples ，请你返回土地的 最小周长 ，使得 至少 有 neededApples 个苹果在土地 里面或者边缘上。

|x| 的值定义为：

• 如果 x >= 0 ，那么值为 x
• 如果 x < 0 ，那么值为 -x

 

示例 1：

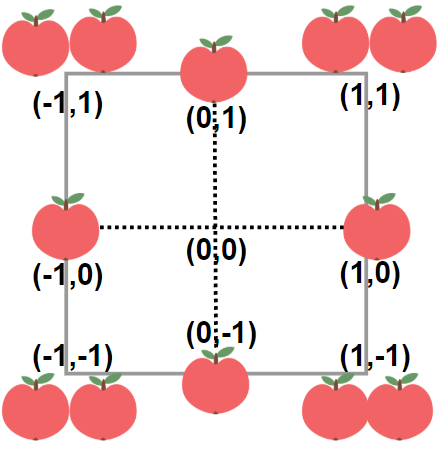
输入：neededApples = 1
输出：8
解释：边长长度为 1 的正方形不包含任何苹果。
但是边长为 2 的正方形包含 12 个苹果（如上图所示）。
周长为 2 * 4 = 8 。

示例 2：

输入：neededApples = 13
输出：16

示例 3：

输入：neededApples = 1000000000
输出：5040

 

提示：

• 1 <= neededApples <= 1015

通过代码

高赞题解

方法一：枚举

提示 $1$

如果正方形土地的右上角坐标为 $(n, n)$，即边长为 $2n$，周长为 $8n$，那么其中包含的苹果总数为：

$$
S_n = 2n(n+1)(2n+1)
$$

提示 $1$ 解释

对于坐标为 $(x, y)$ 的树，它有 $|x| + |y|$ 个苹果。因此，一块右上角坐标为 $(n, n)$ 的正方形土地包含的苹果总数为：

$$
S_n = \sum_{x=-n}^n \sum_{y=-n}^n |x| + |y|
$$

由于 $x$ 和 $y$ 是对称的，因此：

$$
\begin{aligned}
S_n &= 2 \sum_{x=-n}^n \sum_{y=-n}^n |x| \
&= 2 \sum_{x=-n}^n (2n+1) |x| \
&= 2(2n+1) \sum_{x=-n}^n |x| \
&= 2n(n+1)(2n+1)
\end{aligned}
$$

思路与算法

我们从小到大枚举 $n$，直到 $2n(n+1)(2n+1) \geq \textit{neededApples}$ 为止。

代码

[sol1-C++]
class Solution {
public:
    long long minimumPerimeter(long long neededApples) {
        long long n = 1;
        for(; 2 * n * (n + 1) * (2 * n + 1) < neededApples; ++n);
        return n * 8;
    }
};

[sol1-Python3]
class Solution:
    def minimumPerimeter(self, neededApples: int) -> int:
        n = 1
        while 2 * n * (n + 1) * (2 * n + 1) < neededApples:
            n += 1
        return n * 8

复杂度分析

• 时间复杂度：$O(m^{1/3})$，其中 $m$ 表示题目中的 $\textit{neededApples}$。可以发现，$S_n$ 是关于 $n$ 的三次函数，因此需要枚举的 $n$ 的数量级为 $O(m^{1/3})$。

• 空间复杂度：$O(1)$。

方法二：二分查找

思路与算法

由于 $S_n$ 是随着 $n$ 单调递增的，那么我们可以通过二分查找的方法，找出最小的满足 $S_n \geq \textit{neededApples}$ 的 $n$ 值即为答案。

细节

二分查找的下界可以直接置为 $1$，而上界 $\textit{right}$ 需要保证有 $S_\textit{right} \geq \textit{neededApples}$。根据方法一，我们只需要令 $\textit{right} = \lfloor \textit{neededApples}^{1/3} \rfloor$ 即可，其中 $\lfloor \cdot \rfloor$ 表示向下取整。但由于大部分语言中立方根运算较难实现，在实际的编码中，我们可以取一个更加宽松的上界，例如 $\textit{neededApples}^{1/3}$ 最大值 $10^{15}$ 的立方根 $10^5$。

代码

[sol2-C++]
class Solution {
public:
    long long minimumPerimeter(long long neededApples) {
        long long left = 1, right = 100000, ans = 0;
        while (left <= right) {
            long long mid = (left + right) / 2;
            if (2 * mid * (mid + 1) * (mid * 2 + 1) >= neededApples) {
                ans = mid;
                right = mid - 1;
            }
            else {
                left = mid + 1;
            }
        }
        return ans * 8;
    }
};

[sol2-Python3]
class Solution:
    def minimumPerimeter(self, neededApples: int) -> int:
        left, right, ans = 1, 100000, 0
        while left <= right:
            mid = (left + right) // 2
            if 2 * mid * (mid + 1) * (mid * 2 + 1) >= neededApples:
                ans = mid
                right = mid - 1
            else:
                left = mid + 1
        return ans * 8

复杂度分析

• 时间复杂度：$O(\log m)$，其中 $m$ 表示题目中的 $\textit{neededApples}$，即为二分查找需要的时间。

• 空间复杂度：$O(1)$。

统计信息

通过次数	提交次数	AC比率
4334	9066	47.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言