原文链接: https://leetcode-cn.com/problems/maximum-matrix-sum

英文原文

You are given an n x n integer matrix. You can do the following operation any number of times:

• Choose any two adjacent elements of matrix and multiply each of them by -1.

Two elements are considered adjacent if and only if they share a border.

Your goal is to maximize the summation of the matrix's elements. Return the maximum sum of the matrix's elements using the operation mentioned above.

 

Example 1:

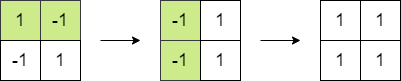
Input: matrix = [[1,-1],[-1,1]]
Output: 4
Explanation: We can follow the following steps to reach sum equals 4:
- Multiply the 2 elements in the first row by -1.
- Multiply the 2 elements in the first column by -1.

Example 2:

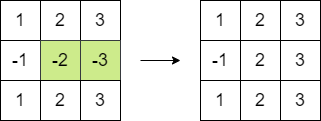
Input: matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
Output: 16
Explanation: We can follow the following step to reach sum equals 16:
- Multiply the 2 last elements in the second row by -1.

 

Constraints:

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

中文题目

给你一个 n x n 的整数方阵 matrix 。你可以执行以下操作 任意次 ：

• 选择 matrix 中 相邻 两个元素，并将它们都 乘以 -1 。

如果两个元素有 公共边 ，那么它们就是 相邻 的。

你的目的是 最大化 方阵元素的和。请你在执行以上操作之后，返回方阵的 最大 和。

 

示例 1：

输入：matrix = [[1,-1],[-1,1]]
输出：4
解释：我们可以执行以下操作使和等于 4 ：
- 将第一行的 2 个元素乘以 -1 。
- 将第一列的 2 个元素乘以 -1 。

示例 2：

输入：matrix = [[1,2,3],[-1,-2,-3],[1,2,3]]
输出：16
解释：我们可以执行以下操作使和等于 16 ：
- 将第二行的最后 2 个元素乘以 -1 。

 

提示：

• n == matrix.length == matrix[i].length
• 2 <= n <= 250
• -105 <= matrix[i][j] <= 105

通过代码

高赞题解

5835. 最大方阵和

第二题

刚开始我用了深度搜索，结果越写越觉得不对劲，最后发现：

其实如果负数数量是双数，我们总是能把他们都翻成正数

如果负数数量是单数，我们怎么翻都会至少留下一个负数

以上，记录下矩阵里绝对值最小的数即可

（我是笨比）

模拟

class Solution {
public:
    long long maxMatrixSum(vector<vector<int>>& matrix) {
        int minn = abs(matrix[0][0]);
        long long ans = 0;
        bool flag = false; //记录是负数的个数是单数还是双数
        for(auto &vec: matrix)
            for(int num: vec){
                if(num < 0){  //是负数的话
                    flag = !flag;  
                    num = -num;  //取绝对值
                }
                ans += num;  //记录绝对值的和
                minn = min(num, minn);  //记录最小值
            }
        if(flag) //是单数
        return ans - 2 * minn;
        return ans;//是双数
    }
};

统计信息

通过次数	提交次数	AC比率
3161	8185	38.6%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言