原文链接: https://leetcode-cn.com/problems/number-of-ways-to-arrive-at-destination

英文原文

You are in a city that consists of n intersections numbered from 0 to n - 1 with bi-directional roads between some intersections. The inputs are generated such that you can reach any intersection from any other intersection and that there is at most one road between any two intersections.

You are given an integer n and a 2D integer array roads where roads[i] = [ui, vi, timei] means that there is a road between intersections ui and vi that takes timei minutes to travel. You want to know in how many ways you can travel from intersection 0 to intersection n - 1 in the shortest amount of time.

Return the number of ways you can arrive at your destination in the shortest amount of time. Since the answer may be large, return it modulo 109 + 7.

 

Example 1:

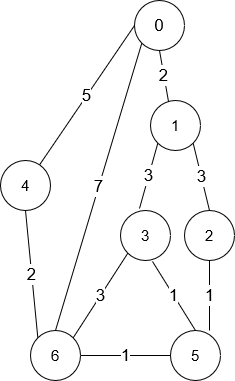
Input: n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
Output: 4
Explanation: The shortest amount of time it takes to go from intersection 0 to intersection 6 is 7 minutes.
The four ways to get there in 7 minutes are:
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

Example 2:

Input: n = 2, roads = [[1,0,10]]
Output: 1
Explanation: There is only one way to go from intersection 0 to intersection 1, and it takes 10 minutes.

 

Constraints:

• 1 <= n <= 200
• n - 1 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 3
• 0 <= ui, vi <= n - 1
• 1 <= timei <= 109
• ui != vi
• There is at most one road connecting any two intersections.
• You can reach any intersection from any other intersection.

中文题目

你在一个城市里，城市由 n 个路口组成，路口编号为 0 到 n - 1 ，某些路口之间有 双向 道路。输入保证你可以从任意路口出发到达其他任意路口，且任意两个路口之间最多有一条路。

给你一个整数 n 和二维整数数组 roads ，其中 roads[i] = [ui, vi, timei] 表示在路口 ui 和 vi 之间有一条需要花费 timei 时间才能通过的道路。你想知道花费 最少时间 从路口 0 出发到达路口 n - 1 的方案数。

请返回花费 最少时间 到达目的地的 路径数目 。由于答案可能很大，将结果对 109 + 7 取余 后返回。

 

示例 1：

输入：n = 7, roads = [[0,6,7],[0,1,2],[1,2,3],[1,3,3],[6,3,3],[3,5,1],[6,5,1],[2,5,1],[0,4,5],[4,6,2]]
输出：4
解释：从路口 0 出发到路口 6 花费的最少时间是 7 分钟。
四条花费 7 分钟的路径分别为：
- 0 ➝ 6
- 0 ➝ 4 ➝ 6
- 0 ➝ 1 ➝ 2 ➝ 5 ➝ 6
- 0 ➝ 1 ➝ 3 ➝ 5 ➝ 6

示例 2：

输入：n = 2, roads = [[1,0,10]]
输出：1
解释：只有一条从路口 0 到路口 1 的路，花费 10 分钟。

 

提示：

• 1 <= n <= 200
• n - 1 <= roads.length <= n * (n - 1) / 2
• roads[i].length == 3
• 0 <= ui, vi <= n - 1
• 1 <= timei <= 109
• ui != vi
• 任意两个路口之间至多有一条路。
• 从任意路口出发，你能够到达其他任意路口。

通过代码

高赞题解

求 $0$ 到其余点的最短路。由于图中边权均为正，所有在最短路上的边构成了一个有向无环图（DAG）。我们在 DAG 上跑拓扑排序，同时计算最短路方案数。

由于输入可以是稠密图，这里可以用邻接矩阵存图，且不需要用堆优化的 Dijkstra。

func countPaths(n int, roads [][]int) (ans int) {
	g := make([][]int, n)
	for i := range g {
		g[i] = make([]int, n)
		for j := range g[i] {
			g[i][j] = 1e18
		}
	}
	for _, r := range roads {
		v, w, wt := r[0], r[1], r[2]
		g[v][w] = wt
		g[w][v] = wt
	}

	// 求 0 到其余点的最短路
	d := make([]int, n)
	for i := range d {
		d[i] = 1e18
	}
	d[0] = 0
	used := make([]bool, n)
	for {
		v := -1
		for w, u := range used {
			if !u && (v < 0 || d[w] < d[v]) {
				v = w
			}
		}
		if v < 0 {
			break
		}
		used[v] = true
		for w, wt := range g[v] {
			if newD := d[v] + wt; newD < d[w] {
				d[w] = newD
			}
		}
	}

	// 最短路构成了一个 DAG，这里不需要建一个新图，直接根据距离来判断每条边是否在 DAG 上
	// 计算 DAG 的入度数组
	deg := make([]int, n)
	for v, r := range g {
		for w, wt := range r {
			if d[v]+wt == d[w] { // 这条边在 DAG 上
				deg[w]++
			}
		}
	}

	// 在 DAG 上跑拓扑排序
	dp := make([]int, n) // dp[i] 表示 0 到 i 的最短路个数
	dp[0] = 1
	q := []int{0}
	for len(q) > 0 {
		v := q[0]
		q = q[1:]
		for w, wt := range g[v] {
			if d[v]+wt == d[w] { // 这条边在 DAG 上
				dp[w] = (dp[w] + dp[v]) % (1e9 + 7)
				if deg[w]--; deg[w] == 0 {
					q = append(q, w)
				}
			}
		}
	}
	return dp[n-1]
}

统计信息

通过次数	提交次数	AC比率
2238	7514	29.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言