原文链接: https://leetcode-cn.com/problems/minimize-the-difference-between-target-and-chosen-elements

英文原文

You are given an m x n integer matrix mat and an integer target.

Choose one integer from each row in the matrix such that the absolute difference between target and the sum of the chosen elements is minimized.

Return the minimum absolute difference.

The absolute difference between two numbers a and b is the absolute value of a - b.

 

Example 1:

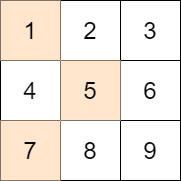
Input: mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
Output: 0
Explanation: One possible choice is to:
- Choose 1 from the first row.
- Choose 5 from the second row.
- Choose 7 from the third row.
The sum of the chosen elements is 13, which equals the target, so the absolute difference is 0.

Example 2:

Input: mat = [[1],[2],[3]], target = 100
Output: 94
Explanation: The best possible choice is to:
- Choose 1 from the first row.
- Choose 2 from the second row.
- Choose 3 from the third row.
The sum of the chosen elements is 6, and the absolute difference is 94.

Example 3:

Input: mat = [[1,2,9,8,7]], target = 6
Output: 1
Explanation: The best choice is to choose 7 from the first row.
The absolute difference is 1.

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 70
• 1 <= mat[i][j] <= 70
• 1 <= target <= 800

中文题目

给你一个大小为 m x n 的整数矩阵 mat 和一个整数 target 。

从矩阵的 每一行 中选择一个整数，你的目标是 最小化 所有选中元素之 和 与目标值 target 的 绝对差 。

返回 最小的绝对差 。

a 和 b 两数字的 绝对差 是 a - b 的绝对值。

 

示例 1：

输入：mat = [[1,2,3],[4,5,6],[7,8,9]], target = 13
输出：0
解释：一种可能的最优选择方案是：
- 第一行选出 1
- 第二行选出 5
- 第三行选出 7
所选元素的和是 13 ，等于目标值，所以绝对差是 0 。

示例 2：

输入：mat = [[1],[2],[3]], target = 100
输出：94
解释：唯一一种选择方案是：
- 第一行选出 1
- 第二行选出 2
- 第三行选出 3
所选元素的和是 6 ，绝对差是 94 。

示例 3：

输入：mat = [[1,2,9,8,7]], target = 6
输出：1
解释：最优的选择方案是选出第一行的 7 。
绝对差是 1 。

 

提示：

• m == mat.length
• n == mat[i].length
• 1 <= m, n <= 70
• 1 <= mat[i][j] <= 70
• 1 <= target <= 800

通过代码

高赞题解

按行dp，枚举当前行所选物品，转移状态。可以压位优化。
具体来说，dp状态定义F[i][j]表示前i行选完，能否凑出和为j的方案
转移就是F[i][j]|=F[i-1][j-A[i][k]]，A[i][k]就是枚举的当前行所选物品

class Solution {
public:
    int minimizeTheDifference(vector<vector<int>>& A, int target) {
        int n=A.size();
        int m=A[0].size();
        bitset<5000> F[n];
        F[0]=0;
        for (int i=0;i<m;++i) F[0][A[0][i]]=1;
        for (int i=1;i<n;++i)
        {
            F[i]=0;
            for (int j=0;j<m;++j)
                F[i]|=F[i-1]<<A[i][j];
        }
        int ans=4900;
        for (int i=1;i<=4900;++i)
            if (F[n-1][i])
                ans=min(ans,abs(target-i));
        return ans;
    }
};

统计信息

通过次数	提交次数	AC比率
4708	15593	30.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言