原文链接: https://leetcode-cn.com/problems/detect-squares

英文原文

You are given a stream of points on the X-Y plane. Design an algorithm that:

• Adds new points from the stream into a data structure. Duplicate points are allowed and should be treated as different points.
• Given a query point, counts the number of ways to choose three points from the data structure such that the three points and the query point form an axis-aligned square with positive area.

An axis-aligned square is a square whose edges are all the same length and are either parallel or perpendicular to the x-axis and y-axis.

Implement the DetectSquares class:

• DetectSquares() Initializes the object with an empty data structure.
• void add(int[] point) Adds a new point point = [x, y] to the data structure.
• int count(int[] point) Counts the number of ways to form axis-aligned squares with point point = [x, y] as described above.

 

Example 1:

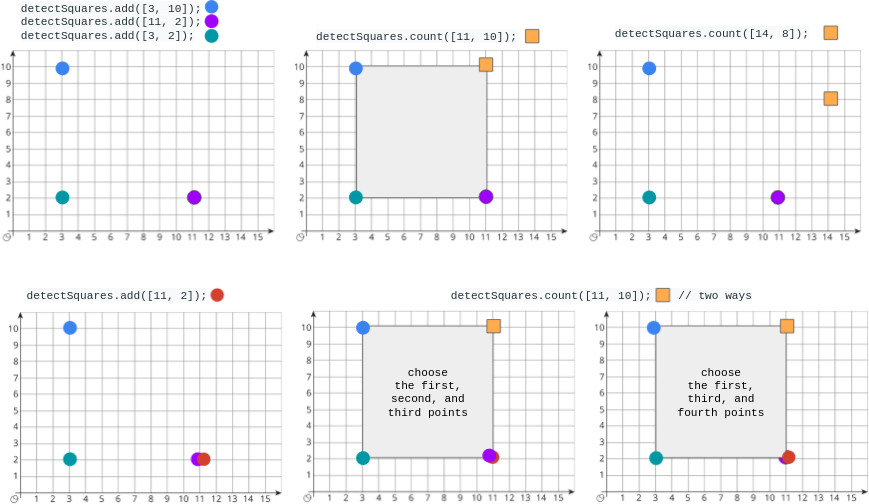
Input
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
Output
[null, null, null, null, 1, 0, null, 2]

Explanation
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // return 1. You can choose:
                               //   - The first, second, and third points
detectSquares.count([14, 8]);  // return 0. The query point cannot form a square with any points in the data structure.
detectSquares.add([11, 2]);    // Adding duplicate points is allowed.
detectSquares.count([11, 10]); // return 2. You can choose:
                               //   - The first, second, and third points
                               //   - The first, third, and fourth points

 

Constraints:

• point.length == 2
• 0 <= x, y <= 1000
• At most 3000 calls in total will be made to add and count.

中文题目

给你一个在 X-Y 平面上的点构成的数据流。设计一个满足下述要求的算法：

• 添加 一个在数据流中的新点到某个数据结构中。可以添加 重复 的点，并会视作不同的点进行处理。
• 给你一个查询点，请你从数据结构中选出三个点，使这三个点和查询点一同构成一个 面积为正 的 轴对齐正方形 ，统计 满足该要求的方案数目。

轴对齐正方形 是一个正方形，除四条边长度相同外，还满足每条边都与 x-轴 或 y-轴 平行或垂直。

实现 DetectSquares 类：

• DetectSquares() 使用空数据结构初始化对象
• void add(int[] point) 向数据结构添加一个新的点 point = [x, y]
• int count(int[] point) 统计按上述方式与点 point = [x, y] 共同构造 轴对齐正方形 的方案数。

 

示例：

输入：
["DetectSquares", "add", "add", "add", "count", "count", "add", "count"]
[[], [[3, 10]], [[11, 2]], [[3, 2]], [[11, 10]], [[14, 8]], [[11, 2]], [[11, 10]]]
输出：
[null, null, null, null, 1, 0, null, 2]

解释：
DetectSquares detectSquares = new DetectSquares();
detectSquares.add([3, 10]);
detectSquares.add([11, 2]);
detectSquares.add([3, 2]);
detectSquares.count([11, 10]); // 返回 1 。你可以选择：
                               //   - 第一个，第二个，和第三个点
detectSquares.count([14, 8]);  // 返回 0 。查询点无法与数据结构中的这些点构成正方形。
detectSquares.add([11, 2]);    // 允许添加重复的点。
detectSquares.count([11, 10]); // 返回 2 。你可以选择：
                               //   - 第一个，第二个，和第三个点
                               //   - 第一个，第三个，和第四个点

 

提示：

• point.length == 2
• 0 <= x, y <= 1000
• 调用 add 和 count 的 总次数 最多为 5000

通过代码

高赞题解

穷举

class DetectSquares {
    Map<String, Integer> map = new HashMap<>();

    public DetectSquares() {

    }

    public void add(int[] point) {
        String key = point[0] + "," + point[1];
        map.put(key, map.getOrDefault(key, 0) + 1);
    }

    public int count(int[] point) {
        // 只找下方对角线的点
        int res = 0;
        int x = point[0];
        int y = point[1];
        for (String key : map.keySet()) {
            int delX = Integer.parseInt(key.split(",")[0]);
            int delY = Integer.parseInt(key.split(",")[1]);
            int delCnt = map.get(key);
            if (delX != x && delY != y && Math.abs(delX - x) == Math.abs(delY - y) && delCnt > 0) {
                // 计算平行X的点(delX, y)和平行Y的点(x, delY)个数
                int xParCnt = map.getOrDefault(delX + "," + y, 0);
                int yParCnt = map.getOrDefault(x + "," + delY, 0);
                res += delCnt * xParCnt * yParCnt;
            }
        }
        return res;
    }
}

统计信息

通过次数	提交次数	AC比率
2954	8741	33.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言