原文链接: https://leetcode-cn.com/problems/the-time-when-the-network-becomes-idle
英文原文
There is a network of n servers, labeled from 0 to n - 1. You are given a 2D integer array edges, where edges[i] = [ui, vi] indicates there is a message channel between servers ui and vi, and they can pass any number of messages to each other directly in one second. You are also given a 0-indexed integer array patience of length n.
All servers are connected, i.e., a message can be passed from one server to any other server(s) directly or indirectly through the message channels.
The server labeled 0 is the master server. The rest are data servers. Each data server needs to send its message to the master server for processing and wait for a reply. Messages move between servers optimally, so every message takes the least amount of time to arrive at the master server. The master server will process all newly arrived messages instantly and send a reply to the originating server via the reversed path the message had gone through.
At the beginning of second 0, each data server sends its message to be processed. Starting from second 1, at the beginning of every second, each data server will check if it has received a reply to the message it sent (including any newly arrived replies) from the master server:
- If it has not, it will resend the message periodically. The data server
iwill resend the message everypatience[i]second(s), i.e., the data serveriwill resend the message ifpatience[i]second(s) have elapsed since the last time the message was sent from this server. - Otherwise, no more resending will occur from this server.
The network becomes idle when there are no messages passing between servers or arriving at servers.
Return the earliest second starting from which the network becomes idle.
Example 1:
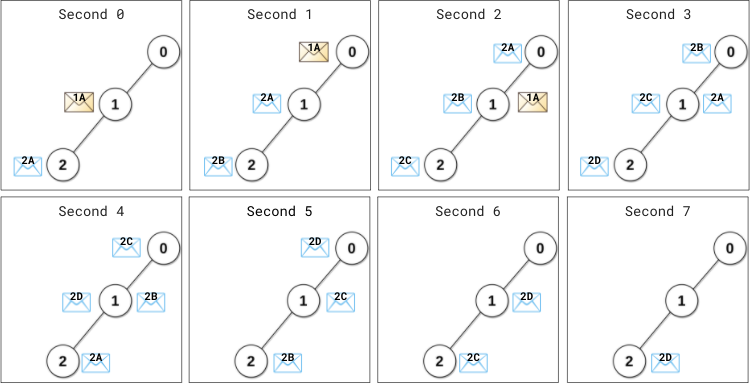
Input: edges = [[0,1],[1,2]], patience = [0,2,1] Output: 8 Explanation: At (the beginning of) second 0, - Data server 1 sends its message (denoted 1A) to the master server. - Data server 2 sends its message (denoted 2A) to the master server.At second 1,
- Message 1A arrives at the master server. Master server processes message 1A instantly and sends a reply 1A back.
- Server 1 has not received any reply. 1 second (1 < patience[1] = 2) elapsed since this server has sent the message, therefore it does not resend the message.
- Server 2 has not received any reply. 1 second (1 == patience[2] = 1) elapsed since this server has sent the message, therefore it resends the message (denoted 2B).
At second 2,
- The reply 1A arrives at server 1. No more resending will occur from server 1.
- Message 2A arrives at the master server. Master server processes message 2A instantly and sends a reply 2A back.
- Server 2 resends the message (denoted 2C).
…
At second 4, - The reply 2A arrives at server 2. No more resending will occur from server 2.
…
At second 7, reply 2D arrives at server 2.
Starting from the beginning of the second 8, there are no messages passing between servers or arriving at servers.
This is the time when the network becomes idle.
Example 2:
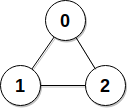
Input: edges = [[0,1],[0,2],[1,2]], patience = [0,10,10] Output: 3 Explanation: Data servers 1 and 2 receive a reply back at the beginning of second 2. From the beginning of the second 3, the network becomes idle.
Constraints:
n == patience.length2 <= n <= 105patience[0] == 01 <= patience[i] <= 105for1 <= i < n1 <= edges.length <= min(105, n * (n - 1) / 2)edges[i].length == 20 <= ui, vi < nui != vi- There are no duplicate edges.
- Each server can directly or indirectly reach another server.
中文题目
给你一个有 n 个服务器的计算机网络,服务器编号为 0 到 n - 1 。同时给你一个二维整数数组 edges ,其中 edges[i] = [ui, vi] 表示服务器 ui 和 vi 之间有一条信息线路,在 一秒 内它们之间可以传输 任意 数目的信息。再给你一个长度为 n 且下标从 0 开始的整数数组 patience 。
题目保证所有服务器都是 相通 的,也就是说一个信息从任意服务器出发,都可以通过这些信息线路直接或间接地到达任何其他服务器。
编号为 0 的服务器是 主 服务器,其他服务器为 数据 服务器。每个数据服务器都要向主服务器发送信息,并等待回复。信息在服务器之间按 最优 线路传输,也就是说每个信息都会以 最少时间 到达主服务器。主服务器会处理 所有 新到达的信息并 立即 按照每条信息来时的路线 反方向 发送回复信息。
在 0 秒的开始,所有数据服务器都会发送各自需要处理的信息。从第 1 秒开始,每 一秒最 开始 时,每个数据服务器都会检查它是否收到了主服务器的回复信息(包括新发出信息的回复信息):
- 如果还没收到任何回复信息,那么该服务器会周期性 重发 信息。数据服务器
i每patience[i]秒都会重发一条信息,也就是说,数据服务器i在上一次发送信息给主服务器后的patience[i]秒 后 会重发一条信息给主服务器。 - 否则,该数据服务器 不会重发 信息。
当没有任何信息在线路上传输或者到达某服务器时,该计算机网络变为 空闲 状态。
请返回计算机网络变为 空闲 状态的 最早秒数 。
示例 1:

输入:edges = [[0,1],[1,2]], patience = [0,2,1] 输出:8 解释: 0 秒最开始时, - 数据服务器 1 给主服务器发出信息(用 1A 表示)。 - 数据服务器 2 给主服务器发出信息(用 2A 表示)。 1 秒时, - 信息 1A 到达主服务器,主服务器立刻处理信息 1A 并发出 1A 的回复信息。 - 数据服务器 1 还没收到任何回复。距离上次发出信息过去了 1 秒(1 < patience[1] = 2),所以不会重发信息。 - 数据服务器 2 还没收到任何回复。距离上次发出信息过去了 1 秒(1 == patience[2] = 1),所以它重发一条信息(用 2B 表示)。 2 秒时, - 回复信息 1A 到达服务器 1 ,服务器 1 不会再重发信息。 - 信息 2A 到达主服务器,主服务器立刻处理信息 2A 并发出 2A 的回复信息。 - 服务器 2 重发一条信息(用 2C 表示)。 ... 4 秒时, - 回复信息 2A 到达服务器 2 ,服务器 2 不会再重发信息。 ... 7 秒时,回复信息 2D 到达服务器 2 。 从第 8 秒开始,不再有任何信息在服务器之间传输,也不再有信息到达服务器。 所以第 8 秒是网络变空闲的最早时刻。
示例 2:

输入:edges = [[0,1],[0,2],[1,2]], patience = [0,10,10] 输出:3 解释:数据服务器 1 和 2 第 2 秒初收到回复信息。 从第 3 秒开始,网络变空闲。
提示:
n == patience.length2 <= n <= 105patience[0] == 0- 对于
1 <= i < n,满足1 <= patience[i] <= 105 1 <= edges.length <= min(105, n * (n - 1) / 2)edges[i].length == 20 <= ui, vi < nui != vi- 不会有重边。
- 每个服务器都直接或间接与别的服务器相连。
通过代码
高赞题解
大家好,我是小爱,一个热爱算法并不断努力的女孩子!关注我,和我一起交流算法心得呀!
解法:广度优先搜索 + 数学推导
我们假设某服务器 $i$ 向主服务器传输信息需要的时间为 $time$,那么其收到反馈信息的时间为 $2 \times time$。在 $[1, 2 \times time - 1]$ 秒内,该数据服务器每 patience[i] 秒重发一次信息,所以共重发了 $count = (2 \times time - 1)/ \ patience[i]$ 次信息。最后一次信息的发送时间为第 $count \times patience[i]$ 秒,该信息需要再经过一次主服务器反馈并返回服务器 $i$ ,到达时间为 $count \times patience[i] + 2 \times time$。
由此,我们遍历所有数据服务器,取所有这些服务器接收到最后一条反馈信息的时间中的最大值,该时间的下一秒网络就会空闲。
遍历所有数据服务器,我们可以先通过邻接表建图,并从主服务器 $0$ 开始,利用广度优先搜索即可。
算法细节:
具体见代码注释
代码:
class Solution {
public:
int networkBecomesIdle(vector<vector<int>>& edges, vector<int>& p) {
int n = p.size();
// 邻接表建图
vector<vector<int>> e(n);
for(auto &ed : edges) {
e[ed[0]].push_back(ed[1]);
e[ed[1]].push_back(ed[0]);
}
// 记录哪些服务器已被扩展
vector<bool> vis(n);
queue<pair<int, int>> q;
q.emplace(0, 0);
vis[0] = true;
// 记录最晚到达时间
int ret = 0;
// 广度优先搜索
while(!q.empty()) {
auto [c, time] = q.front();
q.pop();
if(c != 0) {
// c != 0 是因为首先会扩展到主服务器
int cost = ((2 * time - 1) / p[c]) * p[c] + 2 * time;
ret = max(ret, cost);
}
// 扩展所有与当前数据服务器直接相连的服务器
for(int &next : e[c]) {
if(!vis[next]) {
vis[next] = true;
q.emplace(next, time + 1);
}
}
}
return ret + 1;
}
};复杂度分析:
- 时间复杂度:$O(V + E)$
推荐阅读
小爱每周持续推出原创 C++、算法类文章,欢迎大家提出宝贵意见呀!

C++ 类 字符串
C++ 类 第二部分
C++ 类 第一部分
C++ 基础语法
树状数组
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 1863 | 5202 | 35.8% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




