英文原文
A critical point in a linked list is defined as either a local maxima or a local minima.
A node is a local maxima if the current node has a value strictly greater than the previous node and the next node.
A node is a local minima if the current node has a value strictly smaller than the previous node and the next node.
Note that a node can only be a local maxima/minima if there exists both a previous node and a next node.
Given a linked list head, return an array of length 2 containing [minDistance, maxDistance] where minDistance is the minimum distance between any two distinct critical points and maxDistance is the maximum distance between any two distinct critical points. If there are fewer than two critical points, return [-1, -1].
Example 1:
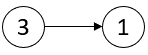
Input: head = [3,1] Output: [-1,-1] Explanation: There are no critical points in [3,1].
Example 2:

Input: head = [5,3,1,2,5,1,2] Output: [1,3] Explanation: There are three critical points: - [5,3,1,2,5,1,2]: The third node is a local minima because 1 is less than 3 and 2. - [5,3,1,2,5,1,2]: The fifth node is a local maxima because 5 is greater than 2 and 1. - [5,3,1,2,5,1,2]: The sixth node is a local minima because 1 is less than 5 and 2. The minimum distance is between the fifth and the sixth node. minDistance = 6 - 5 = 1. The maximum distance is between the third and the sixth node. maxDistance = 6 - 3 = 3.
Example 3:
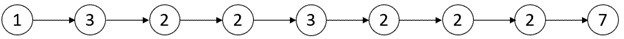
Input: head = [1,3,2,2,3,2,2,2,7] Output: [3,3] Explanation: There are two critical points: - [1,3,2,2,3,2,2,2,7]: The second node is a local maxima because 3 is greater than 1 and 2. - [1,3,2,2,3,2,2,2,7]: The fifth node is a local maxima because 3 is greater than 2 and 2. Both the minimum and maximum distances are between the second and the fifth node. Thus, minDistance and maxDistance is 5 - 2 = 3. Note that the last node is not considered a local maxima because it does not have a next node.
Example 4:
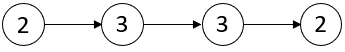
Input: head = [2,3,3,2] Output: [-1,-1] Explanation: There are no critical points in [2,3,3,2].
Constraints:
- The number of nodes in the list is in the range
[2, 105]. 1 <= Node.val <= 105
中文题目
链表中的 临界点 定义为一个 局部极大值点 或 局部极小值点 。
如果当前节点的值 严格大于 前一个节点和后一个节点,那么这个节点就是一个 局部极大值点 。
如果当前节点的值 严格小于 前一个节点和后一个节点,那么这个节点就是一个 局部极小值点 。
注意:节点只有在同时存在前一个节点和后一个节点的情况下,才能成为一个 局部极大值点 / 极小值点 。
给你一个链表 head ,返回一个长度为 2 的数组 [minDistance, maxDistance] ,其中 minDistance 是任意两个不同临界点之间的最小距离,maxDistance 是任意两个不同临界点之间的最大距离。如果临界点少于两个,则返回 [-1,-1] 。
示例 1:

输入:head = [3,1] 输出:[-1,-1] 解释:链表 [3,1] 中不存在临界点。
示例 2:

输入:head = [5,3,1,2,5,1,2] 输出:[1,3] 解释:存在三个临界点: - [5,3,1,2,5,1,2]:第三个节点是一个局部极小值点,因为 1 比 3 和 2 小。 - [5,3,1,2,5,1,2]:第五个节点是一个局部极大值点,因为 5 比 2 和 1 大。 - [5,3,1,2,5,1,2]:第六个节点是一个局部极小值点,因为 1 比 5 和 2 小。 第五个节点和第六个节点之间距离最小。minDistance = 6 - 5 = 1 。 第三个节点和第六个节点之间距离最大。maxDistance = 6 - 3 = 3 。
示例 3:
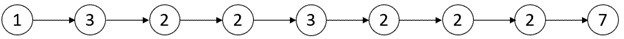
输入:head = [1,3,2,2,3,2,2,2,7] 输出:[3,3] 解释:存在两个临界点: - [1,3,2,2,3,2,2,2,7]:第二个节点是一个局部极大值点,因为 3 比 1 和 2 大。 - [1,3,2,2,3,2,2,2,7]:第五个节点是一个局部极大值点,因为 3 比 2 和 2 大。 最小和最大距离都存在于第二个节点和第五个节点之间。 因此,minDistance 和 maxDistance 是 5 - 2 = 3 。 注意,最后一个节点不算一个局部极大值点,因为它之后就没有节点了。
示例 4:
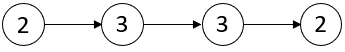
输入:head = [2,3,3,2] 输出:[-1,-1] 解释:链表 [2,3,3,2] 中不存在临界点。
提示:
- 链表中节点的数量在范围
[2, 105]内 1 <= Node.val <= 105
通过代码
高赞题解
思路:
- 链表先转为数组;
- 遍历数组,找到临界点,更新最左侧idx和最右侧的idx;
- 输出临界点的最小距离和最大距离;
int arr[100000]; int* nodesBetweenCriticalPoints(struct ListNode* head, int* returnSize){ int n = 0; while (head != NULL) { /* 链表转为数组 */ arr[n++] = head->val; head = head->next; } int first = -1; int last = -1; int min = INT_MAX; for (int i = 1; i < n - 1; i++) { /* 找到临界点 */ if ((arr[i] > arr[i - 1] && arr[i] > arr[i + 1]) || (arr[i] < arr[i - 1] && arr[i] < arr[i + 1])) { if (first == -1) { /* 记录最左侧的临界点 */ first = i; last = i; } if (i > last) { /* 更新相邻临界点的最小距离 */ min = fmin(min, i - last); } last = i; } } *returnSize = 2; int *res = malloc(sizeof(int) * 2); if (last == first) { /* 不存在两个临界点 */ res[0] = -1; res[1] = -1; } else { /* 输出最小距离和最大距离 */ res[0] = min; res[1] = last - first; } return res; }
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 4989 | 8744 | 57.1% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




