原文链接: https://leetcode-cn.com/problems/minimum-cost-homecoming-of-a-robot-in-a-grid

英文原文

There is an m x n grid, where (0, 0) is the top-left cell and (m - 1, n - 1) is the bottom-right cell. You are given an integer array startPos where startPos = [startrow, startcol] indicates that initially, a robot is at the cell (startrow, startcol). You are also given an integer array homePos where homePos = [homerow, homecol] indicates that its home is at the cell (homerow, homecol).

The robot needs to go to its home. It can move one cell in four directions: left, right, up, or down, and it can not move outside the boundary. Every move incurs some cost. You are further given two 0-indexed integer arrays: rowCosts of length m and colCosts of length n.

• If the robot moves up or down into a cell whose row is r, then this move costs rowCosts[r].
• If the robot moves left or right into a cell whose column is c, then this move costs colCosts[c].

Return the minimum total cost for this robot to return home.

 

Example 1:

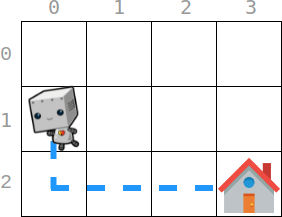
Input: startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
Output: 18
Explanation: One optimal path is that:
Starting from (1, 0)
-> It goes down to (2, 0). This move costs rowCosts[2] = 3.
-> It goes right to (2, 1). This move costs colCosts[1] = 2.
-> It goes right to (2, 2). This move costs colCosts[2] = 6.
-> It goes right to (2, 3). This move costs colCosts[3] = 7.
The total cost is 3 + 2 + 6 + 7 = 18

Example 2:

Input: startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
Output: 0
Explanation: The robot is already at its home. Since no moves occur, the total cost is 0.

 

Constraints:

• m == rowCosts.length
• n == colCosts.length
• 1 <= m, n <= 105
• 0 <= rowCosts[r], colCosts[c] <= 104
• startPos.length == 2
• homePos.length == 2
• 0 <= startrow, homerow < m
• 0 <= startcol, homecol < n

中文题目

给你一个 m x n 的网格图，其中 (0, 0) 是最左上角的格子，(m - 1, n - 1) 是最右下角的格子。给你一个整数数组 startPos ，startPos = [startrow, startcol] 表示 初始 有一个 机器人 在格子 (startrow, startcol) 处。同时给你一个整数数组 homePos ，homePos = [homerow, homecol] 表示机器人的 家 在格子 (homerow, homecol) 处。

机器人需要回家。每一步它可以往四个方向移动：上，下，左，右，同时机器人不能移出边界。每一步移动都有一定代价。再给你两个下标从 0 开始的额整数数组：长度为 m 的数组 rowCosts  和长度为 n 的数组 colCosts 。

• 如果机器人往 上 或者往 下 移动到第 r 行 的格子，那么代价为 rowCosts[r] 。
• 如果机器人往 左 或者往 右 移动到第 c 列 的格子，那么代价为 colCosts[c] 。

请你返回机器人回家需要的 最小总代价 。

 

示例 1：

输入：startPos = [1, 0], homePos = [2, 3], rowCosts = [5, 4, 3], colCosts = [8, 2, 6, 7]
输出：18
解释：一个最优路径为：
从 (1, 0) 开始
-> 往下走到 (2, 0) 。代价为 rowCosts[2] = 3 。
-> 往右走到 (2, 1) 。代价为 colCosts[1] = 2 。
-> 往右走到 (2, 2) 。代价为 colCosts[2] = 6 。
-> 往右走到 (2, 3) 。代价为 colCosts[3] = 7 。
总代价为 3 + 2 + 6 + 7 = 18

示例 2：

输入：startPos = [0, 0], homePos = [0, 0], rowCosts = [5], colCosts = [26]
输出：0
解释：机器人已经在家了，所以不需要移动。总代价为 0 。

 

提示：

• m == rowCosts.length
• n == colCosts.length
• 1 <= m, n <= 105
• 0 <= rowCosts[r], colCosts[c] <= 104
• startPos.length == 2
• homePos.length == 2
• 0 <= startrow, homerow < m
• 0 <= startcol, homecol < n

通过代码

高赞题解

由于 $\textit{rowCosts}$ 和 $\textit{colCosts}$ 的元素均为非负数，所以除了径直走以外的其它策略都不可能更优，那么直接统计径直走的代价即可。

func minCost(startPos, homePos, rowCosts, colCosts []int) int {
	x0, y0, x1, y1 := startPos[0], startPos[1], homePos[0], homePos[1]
	ans := -rowCosts[x0] - colCosts[y0] // 初始的行列无需计算
	if x0 > x1 { x0, x1 = x1, x0 } // 交换位置，保证 x0 <= x1
	if y0 > y1 { y0, y1 = y1, y0 } // 交换位置，保证 y0 <= y1
	for _, cost := range rowCosts[x0 : x1+1] { ans += cost } // 统计答案
	for _, cost := range colCosts[y0 : y1+1] { ans += cost } // 统计答案
	return ans
}

统计信息

通过次数	提交次数	AC比率
2027	4421	45.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言