原文链接: https://leetcode-cn.com/problems/search-a-2d-matrix-ii
英文原文
Write an efficient algorithm that searches for a target value in an m x n integer matrix. The matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example 1:

Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 Output: true
Example 2:
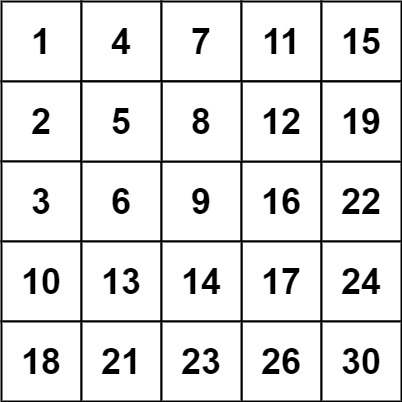
Input: matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 Output: false
Constraints:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- All the integers in each row are sorted in ascending order.
- All the integers in each column are sorted in ascending order.
-109 <= target <= 109
中文题目
编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
示例 1:

输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5 输出:true
示例 2:
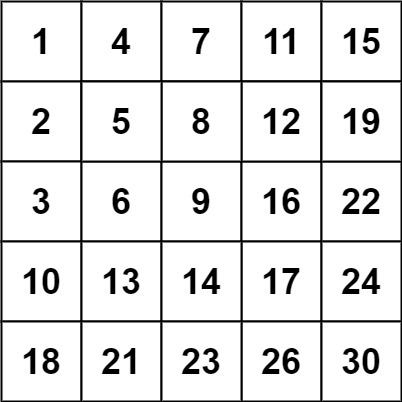
输入:matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20 输出:false
提示:
m == matrix.lengthn == matrix[i].length1 <= n, m <= 300-109 <= matrix[i][j] <= 109- 每行的所有元素从左到右升序排列
- 每列的所有元素从上到下升序排列
-109 <= target <= 109
通过代码
高赞题解
题目描述(中等难度)

矩阵的每行从左到右是升序, 每列从上到下也是升序,在矩阵中查找某个数。
解法一
看到有序,第一反应就是二分查找。最直接的做法,一行一行的进行二分查找即可。
此外,结合有序的性质,一些情况可以提前结束。
比如某一行的第一个元素大于了 target ,当前行和后边的所有行都不用考虑了,直接返回 false。
某一行的最后一个元素小于了 target ,当前行就不用考虑了,换下一行。
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0) {
return false;
}
for (int i = 0; i < matrix.length; i++) {
if (matrix[i][0] > target) {
break;
}
if(matrix[i][matrix[i].length - 1] < target){
continue;
}
int col = binarySearch(matrix[i], target);
if (col != -1) {
return true;
}
}
return false;
}
//二分查找
private int binarySearch(int[] nums, int target) {
int start = 0;
int end = nums.length - 1;
while (start <= end) {
int mid = (start + end) >>> 1;
if (nums[mid] == target) {
return mid;
} else if (nums[mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
return -1;
}
时间复杂度的话,如果是 m 行 n 列,就是 O(mlog(n))。
解法二
参考 这里,需要很敏锐的观察力了。
数组从左到右和从上到下都是升序的,如果从右上角出发开始遍历呢?
会发现每次都是向左数字会变小,向下数字会变大,有点和二分查找树相似。二分查找树的话,是向左数字变小,向右数字变大。
所以我们可以把 target 和当前值比较。
如果
target的值大于当前值,那么就向下走。如果
target的值小于当前值,那么就向左走。如果相等的话,直接返回
true。
也可以换个角度思考。
如果 target 的值小于当前值,也就意味着当前值所在的列肯定不会存在 target 了,可以把当前列去掉,从新的右上角的值开始遍历。
同理,如果 target 的值大于当前值,也就意味着当前值所在的行肯定不会存在 target 了,可以把当前行去掉,从新的右上角的值开始遍历。
看下边的例子。
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
如果 target = 9,如果我们从 15 开始遍历, cur = 15
target < 15, 去掉当前列, cur = 11
[1, 4, 7, 11],
[2, 5, 8, 12],
[3, 6, 9, 16],
[10, 13, 14, 17],
[18, 21, 23, 26]
target < 11, 去掉当前列, cur = 7
[1, 4, 7],
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
target > 7, 去掉当前行, cur = 8
[2, 5, 8],
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
target > 8, 去掉当前行, cur = 9, 遍历结束
[3, 6, 9],
[10, 13, 14],
[18, 21, 23]
不管从哪种角度考虑,代码的话都是一样的。
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0) {
return false;
}
int row = 0;
int col = matrix[0].length - 1;
while (row < matrix.length && col >= 0) {
if (target > matrix[row][col]) {
row++;
} else if (target < matrix[row][col]) {
col--;
} else {
return true;
}
}
return false;
}
时间复杂度就是每个节点最多遍历一遍了,O(m + n)。
解法三
参考 这里 ,还有一种解法。
我的理解的话,算是一种变形的二分法。
二分法的思想就是,目标值和中点值进行比较,然后可以丢弃一半的元素。
这道题的话是矩阵,如果我们找到矩阵的中心,然后和目标值比较看能不能丢弃一些元素。
如下图,中心位置是 9
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, /9/,16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
通过中心位置, 我们可以把原矩形分成四个矩形, 左上, 右上, 左下, 右下
[1, 4, 7 [11, 15
2, 5, 8 12, 19
3, 6, /9/] 16, 22]
[10, 13, 14 [17, 24
[18, 21, 23] 26, 30]
如果 target = 10,
此时中心值小于目标值,左上角矩形中所有的数都小于目标值,我们可以丢弃左上角的矩形,继续从剩下三个矩形中寻找
如果 target = 5,
此时中心值大于目标值,右下角矩形中所有的数都大于目标值,那么我们可以丢弃右下角的矩形,继续从剩下三个矩形中寻找
我们找到了丢弃元素的原则,可以写代码了。
这里的话,矩形我们用左上角和右下角坐标的形式表示,下图是分割后矩形的坐标情况。

我们可以用递归的形式去写,递归出口的话,当矩阵中只有一个元素,直接判断当前元素是不是目标值即可。
还有就是分割的时候可能越界,比如原矩阵只有一行,左下角和右下角的矩阵其实是不存在的,按照上边的坐标公式计算出来后,我们要判断一下是否越界。
public boolean searchMatrix(int[][] matrix, int target) {
if (matrix.length == 0 || matrix[0].length == 0) {
return false;
}
return searchMatrixHelper(matrix, 0, 0, matrix[0].length - 1, matrix.length - 1, matrix[0].length - 1, matrix.length - 1, target);
}
private boolean searchMatrixHelper(int[][] matrix, int x1, int y1, int x2, int y2, int xMax, int yMax, int target) {
//只需要判断左上角坐标即可
if (x1 > xMax || y1 > yMax) {
return false;
}
//x 轴代表的是列,y 轴代表的是行
if(x1 == x2 && y1 == y2){
return matrix[y1][x1] == target;
}
int m1 = (x1 + x2) >>> 1;
int m2 = (y1 + y2) >>> 1;
if (matrix[m2][m1] == target) {
return true;
}
if (matrix[m2][m1] < target) {
// 右上矩阵
return searchMatrixHelper(matrix, m1 + 1, y1, x2, m2, x2, y2, target) ||
// 左下矩阵
searchMatrixHelper(matrix, x1, m2 + 1, m1, y2, x2, y2, target) ||
// 右下矩阵
searchMatrixHelper(matrix, m1 + 1, m2 + 1, x2, y2, x2, y2, target);
} else {
// 右上矩阵
return searchMatrixHelper(matrix, m1 + 1, y1, x2, m2, x2, y2, target) ||
// 左下矩阵
searchMatrixHelper(matrix, x1, m2 + 1, m1, y2, x2, y2, target) ||
// 左上矩阵
searchMatrixHelper(matrix, x1, y1, m1, m2, x2, y2, target);
}
}
总
看到有序数组第一反应就是二分了,也就是解法一。
解法二的话,从右上角开始遍历的想法很妙。
解法三的话思想很简单,就是变形的二分法,每次抛弃一部分元素,但代码的话其实写出来不是很容易,相对于解法一和解法二来说是有些复杂度的。
之前自己在博客总结的,更多题解可以在原地址 https://leetcode.wang。
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 214965 | 433157 | 49.6% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|
相似题目
| 题目 | 难度 |
|---|---|
| 搜索二维矩阵 | 中等 |




