原文链接: https://leetcode-cn.com/problems/range-sum-query-2d-immutable

英文原文

Given a 2D matrix matrix, handle multiple queries of the following type:

Calculate the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Implement the NumMatrix class:

NumMatrix(int[][] matrix) Initializes the object with the integer matrix matrix.
int sumRegion(int row1, int col1, int row2, int col2) Returns the sum of the elements of matrix inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2).

Example 1:

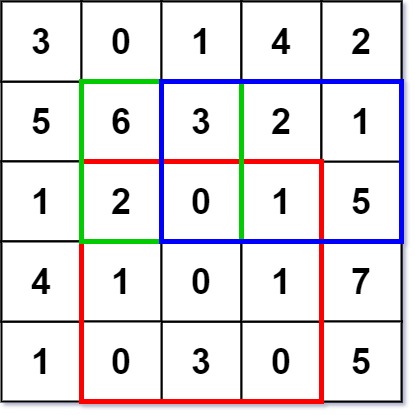
Input
["NumMatrix", "sumRegion", "sumRegion", "sumRegion"]
[[[[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]], [2, 1, 4, 3], [1, 1, 2, 2], [1, 2, 2, 4]]
Output
[null, 8, 11, 12]

Explanation
NumMatrix numMatrix = new NumMatrix([[3, 0, 1, 4, 2], [5, 6, 3, 2, 1], [1, 2, 0, 1, 5], [4, 1, 0, 1, 7], [1, 0, 3, 0, 5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (i.e sum of the red rectangle)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (i.e sum of the green rectangle)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (i.e sum of the blue rectangle)

Constraints:

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁵ <= matrix[i][j] <= 10⁵
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
At most 10⁴ calls will be made to sumRegion.

中文题目

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的 左上角 为 (row1, col1) ，右下角 为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回 左上角 (row1, col1) 、右下角 (row2, col2) 所描述的子矩阵的元素总和。

示例 1：

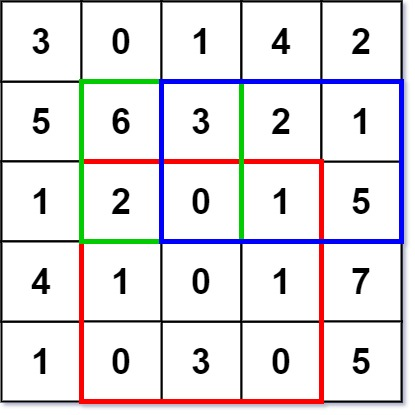
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 200
-10⁵ <= matrix[i][j] <= 10⁵
0 <= row1 <= row2 < m
0 <= col1 <= col2 < n
最多调用 10⁴ 次 sumRegion 方法

通过代码

高赞题解

各位题友大家好！今天是 @负雪明烛 坚持日更的第 37 天。今天力扣上的每日一题是「304. 二维区域和检索 - 矩阵不可变」。

解题思路

做这种初始化一次、检索多次的题目的秘诀：在初始化的时候做预处理。

今天的每日一题让求二维数组中某个子矩形区域的和。很容易看出，今天的题目是 303. 区域和检索 - 数组不可变的升级版。

同样地，今天的题目仍然用 preSum（前缀和）求解，包括两个步骤。

步骤一：求 preSum

我们先从如何求出二维空间的 preSum[i][j]。

我们定义 $preSum[i][j]$ 表示从 $[0,0]$ 位置到 $[i,j]$ 位置的子矩形所有元素之和。
可以用下图帮助理解：

$$S(O, D) = S(O, C) + S(O, B) - S(O, A) + D$$

减去 $S(O, A)$ 的原因是 $S(O, C)$ 和 $S(O, B)$ 中都有 $S(O, A)$，即加了两次 $S(O, A)$，所以需要减去一次 $S(O, A)$。

如果求 $preSum[i][j]$ 表示的话，对应了以下的递推公式：

$$preSum[i][j] = preSum[i - 1][j] + preSum[i][j - 1] - preSum[i - 1][j - 1] + matrix[i][j]$$

步骤二：根据 preSum 求子矩形面积

前面已经求出了数组中从 $[0,0]$ 位置到 $[i,j]$ 位置的 preSum。下面要利用 $preSum[i][j]$ 来快速求出任意子矩形的面积。

同样利用一张图来说明：

$$S(A, D) = S(O, D) - S(O, E) - S(O, F) + S(O, G)$$

加上子矩形 $S(O, G)$ 面积的原因是 $S(O, E)$ 和 $S(O, F)$ 中都有 $S(O, G)$，即减了两次 $S(O, G)$，所以需要加上一次 $S(O, G)$。

如果要求 $[row1, col1]$ 到 $[row2, col2]$ 的子矩形的面积的话，用 preSum 对应了以下的递推公式：

$$preSum[row2][col2] - preSum[row2][col1 - 1] - preSum[row1 - 1][col2] + preSum[row1 - 1][col1 - 1]$$

代码

下面代码实现的时候，使用的 preSum 比原矩阵 matrix 多了一行一列，是为了让第 0 行与第 0 列的元素也能使用上面的递推公式。如果 preSum 矩阵大小和 martix 大小相等，则需要对第 0 行与第 0 列特殊判断。

class NumMatrix:

    def __init__(self, matrix: List[List[int]]):
        if not matrix or not matrix[0]:
            M, N = 0, 0
        else:
            M, N = len(matrix), len(matrix[0])
        self.preSum = [[0] * (N + 1) for _ in range(M + 1)]
        for i in range(M):
            for j in range(N):
                self.preSum[i + 1][j + 1] = self.preSum[i][j + 1] + self.preSum[i + 1][j]  - self.preSum[i][j] + matrix[i][j]


    def sumRegion(self, row1: int, col1: int, row2: int, col2: int) -> int:
        return self.preSum[row2 + 1][col2 + 1] - self.preSum[row2 + 1][col1] - self.preSum[row1][col2 + 1] + self.preSum[row1][col1]

时间复杂度：构造函数的时间复杂度是 $O(M * N)$； sumRegion 函数的时间复杂度是 $O(1)$
空间复杂度：利用了preSum 矩阵，空间是 $O(M * N)$。

刷题心得

一维的 preSum 拓展成二维 preSum 已经学会了，那如果是 N 维的应该怎么处理呢？

OK，以上就是 @负雪明烛写的今天题解的全部内容了，如果你觉得有帮助的话，求赞、求关注、求收藏。如果有疑问的话，请在下面评论，我会及时解答。

关注我，你将不会错过我的精彩动画题解、面试题分享、组队刷题活动，进入主页 @负雪明烛右侧有刷题组织，从此刷题不再孤单。

祝大家牛年大吉！AC 多多，Offer 多多！我们明天再见！

统计信息

通过次数	提交次数	AC比率
67914	122378	55.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
区域和检索 - 数组不可变	简单
二维区域和检索 - 可变	困难

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途