原文链接: https://leetcode-cn.com/problems/verify-preorder-serialization-of-a-binary-tree
英文原文
One way to serialize a binary tree is to use preorder traversal. When we encounter a non-null node, we record the node's value. If it is a null node, we record using a sentinel value such as '#'.
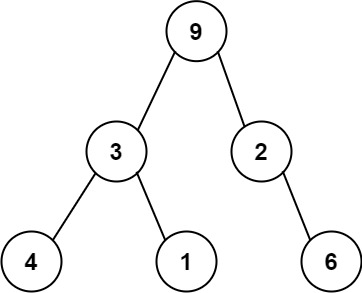
For example, the above binary tree can be serialized to the string "9,3,4,#,#,1,#,#,2,#,6,#,#", where '#' represents a null node.
Given a string of comma-separated values preorder, return true if it is a correct preorder traversal serialization of a binary tree.
It is guaranteed that each comma-separated value in the string must be either an integer or a character '#' representing null pointer.
You may assume that the input format is always valid.
- For example, it could never contain two consecutive commas, such as
"1,,3".
Note: You are not allowed to reconstruct the tree.
Example 1:
Input: preorder = "9,3,4,#,#,1,#,#,2,#,6,#,#" Output: true
Example 2:
Input: preorder = "1,#" Output: false
Example 3:
Input: preorder = "9,#,#,1" Output: false
Constraints:
1 <= preorder.length <= 104preorderconsist of integers in the range[0, 100]and'#'separated by commas','.
中文题目
序列化二叉树的一种方法是使用前序遍历。当我们遇到一个非空节点时,我们可以记录下这个节点的值。如果它是一个空节点,我们可以使用一个标记值记录,例如 #。
_9_
/ \
3 2
/ \ / \
4 1 # 6
/ \ / \ / \
# # # # # #
例如,上面的二叉树可以被序列化为字符串 "9,3,4,#,#,1,#,#,2,#,6,#,#",其中 # 代表一个空节点。
给定一串以逗号分隔的序列,验证它是否是正确的二叉树的前序序列化。编写一个在不重构树的条件下的可行算法。
每个以逗号分隔的字符或为一个整数或为一个表示 null 指针的 '#' 。
你可以认为输入格式总是有效的,例如它永远不会包含两个连续的逗号,比如 "1,,3" 。
示例 1:
输入:"9,3,4,#,#,1,#,#,2,#,6,#,#"输出:true
示例 2:
输入:"1,#"输出:false
示例 3:
输入:"9,#,#,1"输出:false
通过代码
高赞题解
各位题友大家好! 今天是 @负雪明烛 坚持日更的第 47 天。今天力扣上的每日一题是「331. 验证二叉树的前序序列化」。
解题思路
今天题目要我们验证输入字符串是否是有效的二叉树的前序序列化,力扣的二叉树题目的输入都是这种格式的。
本文使用两种方法解决:
- 栈
- 计算入度出度
方法一:栈
栈的思路是「自底向上」的想法。下面要结合本题是「前序遍历」这个重要特点。
我们知道「前序遍历」是按照「根节点-左子树-右子树」的顺序遍历的,只有当根节点的所有左子树遍历完成之后,才会遍历右子树。对于本题的输入,我们可以先判断「左子树」是否有效的,然后再判断「右子树」是否有效的,最后判断「根节点-左子树-右子树」是否为有效的。这个思路类似于递归,而把递归改写成循环时,就会使用「栈」,这就是本题使用「栈」的原因。
下面的重点是如何判断一棵子树是否有效?首先考虑最简单情况:怎么判断一个节点是叶子节点?很明显,当一个节点的两个孩子都是 "#"(空)的时候,该节点就是叶子节点。

当一个节点不是叶子节点的时候,那么它必定至少有一个孩子非空!有两种情况:
- 两个孩子都非
"#"(空); - 一个孩子为
"#"(空),另一个孩子非"#"(空);
为了兼容这两个情况,我们想出了本题的一个重磅级的技巧:把有效的叶子节点使用 "#" 代替。 比如把 4## 替换成 # 。此时,叶子节点会变成空节点!

具体操作流程示例如下:
如输入: "9,3,4,#,#,1,#,#,2,#,6,#,#" ,当遇到 x,#,# 的时候,就把它变为 #。
模拟一遍过程:
[9,3,4,#,#] => [9,3,#],继续[9,3,#,1,#,#] => [9,3,#,#] => [9,#],继续[9,#2,#,6,#,#] => [9,#,2,#,#] => [9,#,#] => [#],结束
下面的动画模拟了"9,3,4,#,#,1,#,#,#"的操作过程:

PPT 如下,可以逐步点击观看:
< ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, >
>
这个操作流程完美结合了「栈」和「前序遍历」的特性,完美!代码如下:
[]class Solution(object): def isValidSerialization(self, preorder): stack = [] for node in preorder.split(','): stack.append(node) while len(stack) >= 3 and stack[-1] == stack[-2] == '#' and stack[-3] != '#': stack.pop(), stack.pop(), stack.pop() stack.append('#') return len(stack) == 1 and stack.pop() == '#'
- 时间复杂度:$O(N)$
- 空间复杂度:$O(N)$
方法二:计算入度出度
背景知识:
- 入度:有多少个节点指向它;
- 出度:它指向多少个节点。
我们知道在树(甚至图)中,所有节点的入度之和等于出度之和。可以根据这个特点判断输入序列是否为有效的!
在一棵二叉树中:
- 每个空节点(
"#")会提供 0 个出度和 1 个入度。 - 每个非空节点会提供 2 个出度和 1 个入度(根节点的入度是 0)。

我们只要把字符串遍历一次,每个节点都累加 diff = 出度 - 入度 。在遍历到任何一个节点的时候,要求diff >= 0,原因是还没遍历到该节点的子节点,所以此时的出度应该大于等于入度。当所有节点遍历完成之后,整棵树的 diff == 0 。
这里解释一下为什么下面的代码中 diff 的初始化为 1。因为,我们加入一个非空节点时,都会对 diff 先减去 1(入度),再加上 2(出度)。但是由于根节点没有父节点,所以其入度为 0,出度为 2。因此 diff 初始化为 1,是为了在加入根节点的时候,diff 先减去 1(入度),再加上 2(出度),此时 diff 正好应该是2.
[]class Solution(object): def isValidSerialization(self, preorder): nodes = preorder.split(',') diff = 1 for node in nodes: diff -= 1 if diff < 0: return False if node != '#': diff += 2 return diff == 0
- 时间复杂度:$O(N)$
- 空间复杂度:$O(1)$
刷题心得
这个题是真的不错,特别是把二叉树的题目和「栈」的应用完美结合,给我很大启发。
参考资料:细语呢喃
OK,以上就是 @负雪明烛 写的今天题解的全部内容了,如果你觉得有帮助的话,求赞、求关注、求收藏。如果有疑问的话,请在下面评论,我会及时解答。
关注我,你将不会错过我的精彩动画题解、面试题分享、组队刷题活动,进入主页 @负雪明烛 右侧有刷题组织,从此刷题不再孤单。
祝大家 AC 多多,Offer 多多!我们明天再见!
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 46373 | 96800 | 47.9% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




