375-猜数字大小 II(Guess Number Higher or Lower II)
发表于：2021-12-03 | 分类： 中等
字数统计: 3.3k | 阅读时长: 14分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/guess-number-higher-or-lower-ii

英文原文

We are playing the Guessing Game. The game will work as follows:

  1. I pick a number between 1 and n.
  2. You guess a number.
  3. If you guess the right number, you win the game.
  4. If you guess the wrong number, then I will tell you whether the number I picked is higher or lower, and you will continue guessing.
  5. Every time you guess a wrong number x, you will pay x dollars. If you run out of money, you lose the game.

Given a particular n, return the minimum amount of money you need to guarantee a win regardless of what number I pick.

 

Example 1:

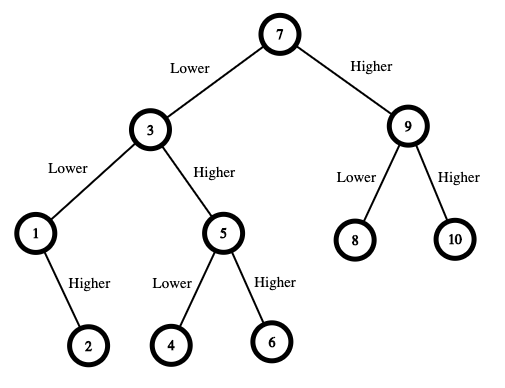
Input: n = 10
Output: 16
Explanation: The winning strategy is as follows:
- The range is [1,10]. Guess 7.
    - If this is my number, your total is $0. Otherwise, you pay $7.
    - If my number is higher, the range is [8,10]. Guess 9.
        - If this is my number, your total is $7. Otherwise, you pay $9.
        - If my number is higher, it must be 10. Guess 10. Your total is $7 + $9 = $16.
        - If my number is lower, it must be 8. Guess 8. Your total is $7 + $9 = $16.
    - If my number is lower, the range is [1,6]. Guess 3.
        - If this is my number, your total is $7. Otherwise, you pay $3.
        - If my number is higher, the range is [4,6]. Guess 5.
            - If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $5.
            - If my number is higher, it must be 6. Guess 6. Your total is $7 + $3 + $5 = $15.
            - If my number is lower, it must be 4. Guess 4. Your total is $7 + $3 + $5 = $15.
        - If my number is lower, the range is [1,2]. Guess 1.
            - If this is my number, your total is $7 + $3 = $10. Otherwise, you pay $1.
            - If my number is higher, it must be 2. Guess 2. Your total is $7 + $3 + $1 = $11.
The worst case in all these scenarios is that you pay $16. Hence, you only need $16 to guarantee a win.

Example 2:

Input: n = 1
Output: 0
Explanation: There is only one possible number, so you can guess 1 and not have to pay anything.

Example 3:

Input: n = 2
Output: 1
Explanation: There are two possible numbers, 1 and 2.
- Guess 1.
    - If this is my number, your total is $0. Otherwise, you pay $1.
    - If my number is higher, it must be 2. Guess 2. Your total is $1.
The worst case is that you pay $1.

 

Constraints:

  • 1 <= n <= 200

中文题目

我们正在玩一个猜数游戏，游戏规则如下：

  1. 我从 1 到 n 之间选择一个数字。
  2. 你来猜我选了哪个数字。
  3. 如果你猜到正确的数字，就会 赢得游戏 。
  4. 如果你猜错了，那么我会告诉你，我选的数字比你的 更大或者更小 ，并且你需要继续猜数。
  5. 每当你猜了数字 x 并且猜错了的时候，你需要支付金额为 x 的现金。如果你花光了钱，就会 输掉游戏 。

给你一个特定的数字 n ，返回能够 确保你获胜 的最小现金数，不管我选择那个数字 。

 

示例 1：

输入：n = 10
输出：16
解释：制胜策略如下：
- 数字范围是 [1,10] 。你先猜测数字为 7 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $7 。
    - 如果我的数字更大，则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $9 。
        - 如果我的数字更大，那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏，总费用为 $7 + $9 = $16 。
        - 如果我的数字更小，那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏，总费用为 $7 + $9 = $16 。
    - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。
        - 如果这是我选中的数字，你的总费用为 $7 。否则，你需要支付 $3 。
        - 如果我的数字更大，则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $5 。
            - 如果我的数字更大，那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
            - 如果我的数字更小，那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏，总费用为 $7 + $3 + $5 = $15 。
        - 如果我的数字更小，则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。
            - 如果这是我选中的数字，你的总费用为 $7 + $3 = $10 。否则，你需要支付 $1 。
            - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $7 + $3 + $1 = $11 。
在最糟糕的情况下，你需要支付 $16 。因此，你只需要 $16 就可以确保自己赢得游戏。

示例 2：

输入：n = 1
输出：0
解释：只有一个可能的数字，所以你可以直接猜 1 并赢得游戏，无需支付任何费用。

示例 3：

输入：n = 2
输出：1
解释：有两个可能的数字 1 和 2 。
- 你可以先猜 1 。
    - 如果这是我选中的数字，你的总费用为 $0 。否则，你需要支付 $1 。
    - 如果我的数字更大，那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏，总费用为 $1 。
最糟糕的情况下，你需要支付 $1 。

 

提示：

  • 1 <= n <= 200

通过代码

高赞题解

1.为什么使用动态规划，不使用二分？

动态规划与二分的区别在哪里呢？
使用动态规划的好处在于我可以穷举所有的情况，对于这个题来说，就是指动态规划的方法可以把每一个数字都当作分割点，而二分只能把中间的数字当作分割点。
举个例子：
当n=5：

动态规划：1 2 3 4 5 在第一次猜数时，我们可以猜1,2,3,4,5
二分查找：1 2 3 4 5 在第一次猜数时，我们只能猜3

为什么要使用动态规划猜所有的数字呢？
当n=5，假如我第一次猜3，那么需要7；假如我第一次猜4，只需要6.
很显然6才是正确答案，使用二分法虽然方便，但是是错误的。所以我使用动态规划穷举所有情况。

2.对于二维数组dp[i][j]的理解

动态规划需要使用内存储存计算过的结果，在这里我使用一个二维数组dp[n+1][n+1]

对于动态规划来说，需要明白dp[i][j]的含义，所以接下来我尝试解释dp[i][j]的含义:
dp[i][j]是说依次以从i到j的数字作为分割点(猜的数)，必定赢的游戏所用钱的最小值。
这样看起来似乎很难理解。

(1)解释dp[1][1]:
dp[1][1]是指只有一个数字1，我们以1作为分割点(猜的数)，赢得游戏所用钱的最小值，一看就知道，dp[1][1]=0。因为我们只能猜1，答案也只能是1，不用花钱

(2)解释dp[1][2]:
dp[1][2]是指只有两个数字1，2
我们先以1作为分割点(猜的数):

猜1：    
答案是1，花费0元
答案是2，花费1元
必定赢得游戏，最多花费1元

我们再以2作为分割点(猜的数):

猜2：
答案是1，花费2元
答案是2，花费0元
必定赢得游戏，最多花费2元

综上，只要进入[1,2]这个区间，我们第一次猜1，只要花费1元，必定可以赢得游戏（假如看不懂，再看一次，细细的品）
所以dp[1][2]=1(只要花1元必定赢得游戏，当第一次猜1时)

(3)解释dp[2][3]:
dp[2][3]是指只有两个数字2，3

有一个小问题，为什么不是从1开始呢？(明白的不用看)
比如n=3，我们第一次猜了1，但是答案是2或者3，反正不是1，我们是不是要到[2,3]区间来寻找答案，即求
dp[2][3]

我们先以2作为分割点(猜的数):

猜2：    
答案是2，花费0元
答案是3，花费2元
必定赢得游戏，最多花费2元

我们再以3作为分割点(猜的数):

猜3：
答案是2，花费3元
答案是3，花费0元
必定赢得游戏，最多花费3元

综上，只要进入[2,3]这个区间，我们第一次猜2，只要花费2元，必定可以赢得游戏
所以dp[2][3]=2(只要花2元必定赢得游戏，当第一次猜2时)

(4)解释dp[1][3]:
dp[1][3]是指只有三个数字1，2，3
我们先以1作为分割点(猜的数):

猜1：
答案是1，花费0元
答案是2或者3，这个时候会进入另一个区间[2,3]，花费1+dp[2][3]元
必定赢得游戏，最多花费max(0,1+dp[2][3])元

我们再以2作为分割点(猜的数):

猜2：
答案是1，花费2+dp[1][1]=2+0=2元
答案是2，花费0元
答案是3，花费2+dp[3][3]=2+0=2元
必定赢得游戏，最多花费max(0,2+dp[1][1],2+dp[3][3])元

我们最后以3作为分割点(猜的数):

猜3：
答案是1或者2,花费3+dp[1][2]元
答案是3，花费0元
必定赢得游戏，最多花费max(0,3+dp[1][2])元

综上，只要进入[1][3]这个区间，我们只要花费min( max(0,1+dp[2][3]) , max(0,2+dp[1][1],2+dp[3][3]) , max(0,3+dp[1][2]) )元必定可以赢的游戏
而dp[1][3]也就等于那个min的值。

可以发现，只要找到dp[1][n]即可。
(假如不能明白dp[i][j]可以返回上面内容看例子，明白后再往下阅读)

3.状态转移方程

状态转移方程怎么写呢？
看第4个例子，dp[1][3]我们就可以发现：
对于每一个分割点，我们取它左右两边区间的最大值加上分割点本身作为取此分割点的dp[i][j]值
对于每一个区间，我们取所有分割点的dp[i][j]的最小值作为dp[i][j]的真正的值
特别地，对于以i作为分割点的dp[i][j]，只取i右边的区间；对于以j作为分割点的dp[i][j]，只取j左边的区间

这个我觉得看懂dp[1][3]不难理解，要是理解不了的话，我这样解释一下(明白的不用看)：

i i+1 i+2 ... ... j-2 j-1 j
以i+1为分割点对应的：dp1=max(dp[i][i],dp[i+2][j])+i+1
以j-1为分割点对应的: dp2=max(dp[i][j-2],dp[j][j])+j-1
特别地,以i为分割点：dp0=i+dp[i+1][j];以j为分割点: dp3=j+dp[i][j-1]
dp[i][j]=min(dp0,dp1,dp2,dp3)

4.数组填充

给出一个dp二维数组来用代码填充它，“\”表示正无穷

(1)初始化：         (2)易知dp[i][i]=0   
| \ \ \ \ |         | 0 \ \ \ |
| \ \ \ \ |         | \ 0 \ \ |
| \ \ \ \ |         | \ \ 0 \ |
| \ \ \ \ |         | \ \ \ 0 |

接下来要考虑怎么填充矩阵以得到dp[1][n]:
很容易我们发现可以用一个位置左边和下边地数据来计算它本身，因此可以这样填充

(3)填充1列：
| 0 1 \ \ |  dp[1][2]计算步骤向上看
| \ 0 \ \ |
| \ \ 0 \ |
| \ \ \ 0 |
(4)再填充1列：
| 0 1 x \ |  dp[1][3]计算步骤向上看
| \ 0 2 \ |  dp[2][3]计算步骤向上看(先填充)
| \ \ 0 \ |
| \ \ \ 0 |
(5)再填充最后一列:
| 0 1 x x |  dp[1][4]计算步骤向上看
| \ 0 2 x |  dp[2][4]计算步骤向上看(然后填充)
| \ \ 0 x |  dp[3][4]计算步骤向上看(先填充)
| \ \ \ 0 |
x都是因为我懒得算了... ... 偷个懒，有兴趣可以自己算

5.代码实现

上述问题搞清楚就可以来写代码了

class Solution {
public:
    int getMoneyAmount(int n) {
        if(n==1)
            return 0;
        //定义矩阵
        int dp[n+1][n+1];
        //初始化“\”
        for(int i=0;i<=n;i++){
            for(int j=0;j<=n;j++){
                dp[i][j]=INT_MAX;
            }
        }
        //定义基础值dp[i][i]
        for(int i=0;i<=n;i++){
            dp[i][i]=0;
        }

        //按列来，从第2列开始
        for(int j=2;j<=n;j++){
            //按行来，从下往上
            for(int i=j-1;i>=1;i--){
                //算除了两端的每一个分割点
                for(int k=i+1;k<=j-1;k++){
                    dp[i][j]=min(k+max(dp[i][k-1],dp[k+1][j]),dp[i][j]);
                }
                //算两端
                dp[i][j]=min(dp[i][j],i+dp[i+1][j]);
                dp[i][j]=min(dp[i][j],j+dp[i][j-1]);
            }
        }
        return dp[1][n];
    }
};

6.反思

第一次写题解，可能写的不好，有问题可以评论我，希望大家看明白，能帮助到大家！
点个赞呗亲

统计信息

通过次数 提交次数 AC比率
34329 57222 60.0%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言

相似题目

题目 难度
翻转游戏 II 中等
猜数字大小 简单
我能赢吗 中等
找到 K 个最接近的元素 中等
动态规划 数学 博弈
上一篇:
374-猜数字大小(Guess Number Higher or Lower)
下一篇:
376-摆动序列(Wiggle Subsequence)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo