378-有序矩阵中第 K 小的元素(Kth Smallest Element in a Sorted Matrix)

原文链接: https://leetcode-cn.com/problems/kth-smallest-element-in-a-sorted-matrix

英文原文

Given an n x n matrix where each of the rows and columns is sorted in ascending order, return the k^th smallest element in the matrix.

Note that it is the k^th smallest element in the sorted order, not the k^th distinct element.

You must find a solution with a memory complexity better than O(n²).

Example 1:

Input: matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
Output: 13
Explanation: The elements in the matrix are [1,5,9,10,11,12,13,13,15], and the 8^th smallest number is 13

Example 2:

Input: matrix = [[-5]], k = 1
Output: -5

Constraints:

n == matrix.length == matrix[i].length
1 <= n <= 300
-10⁹ <= matrix[i][j] <= 10⁹
All the rows and columns of matrix are guaranteed to be sorted in non-decreasing order.
1 <= k <= n²

Follow up:

Could you solve the problem with a constant memory (i.e., O(1) memory complexity)?
Could you solve the problem in O(n) time complexity? The solution may be too advanced for an interview but you may find reading this paper fun.

中文题目

给你一个 n x n 矩阵 matrix ，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是 排序后 的第 k 小元素，而不是第 k 个不同的元素。

示例 1：

输入：matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8
输出：13
解释：矩阵中的元素为 [1,5,9,10,11,12,13,13,15]，第 8 小元素是 13

示例 2：

输入：matrix = [[-5]], k = 1
输出：-5

提示：

n == matrix.length
n == matrix[i].length
1 <= n <= 300
-10⁹ <= matrix[i][j] <= 10⁹
题目数据保证 matrix 中的所有行和列都按 非递减顺序 排列
1 <= k <= n²

通过代码

高赞题解

方法一：直接排序

思路及算法

最直接的做法是将这个二维数组转成一维数组，并对该一维数组进行排序。最后这个一维数组中的第 $k$ 个数即为答案。

代码

[sol1-C++]
class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        vector<int> rec;
        for (auto& row : matrix) {
            for (int it : row) {
                rec.push_back(it);
            }
        }
        sort(rec.begin(), rec.end());
        return rec[k - 1];
    }
};

[sol1-Java]
class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int rows = matrix.length, columns = matrix[0].length;
        int[] sorted = new int[rows * columns];
        int index = 0;
        for (int[] row : matrix) {
            for (int num : row) {
                sorted[index++] = num;
            }
        }
        Arrays.sort(sorted);
        return sorted[k - 1];
    }
}

[sol1-Python3]
class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        rec = sorted(sum(matrix, []))
        return rec[k - 1]

[sol1-Golang]
func kthSmallest(matrix [][]int, k int) int {
    rows, columns := len(matrix), len(matrix[0])
    sorted := make([]int, rows * columns)
    index := 0
    for _, row := range matrix {
        for _, num := range row {
            sorted[index] = num
            index++
        }
    }
    sort.Ints(sorted)
    return sorted[k-1]
}

[sol1-C]
int cmp(const void *a, const void *b) { return (*(int *)a - *(int *)b); }

int kthSmallest(int **matrix, int matrixSize, int *matrixColSize, int k) {
    int *rec = (int *)malloc(matrixSize * matrixSize * sizeof(int));

    int num = 0;
    for (int i = 0; i < matrixSize; i++) {
        for (int j = 0; j < matrixColSize[i]; j++) {
            rec[num++] = matrix[i][j];
        }
    }
    qsort(rec, num, sizeof(int), cmp);

    return rec[k - 1];
}

复杂度分析

时间复杂度：$O(n^2\log{n})$，对 $n^2$ 个数排序。
空间复杂度：$O(n^2)$，一维数组需要存储这 $n^2$ 个数。

方法二：归并排序

思路及算法

由题目给出的性质可知，这个矩阵的每一行均为一个有序数组。问题即转化为从这 $n$ 个有序数组中找第 $k$ 大的数，可以想到利用归并排序的做法，归并到第 $k$ 个数即可停止。

一般归并排序是两个数组归并，而本题是 $n$ 个数组归并，所以需要用小根堆维护，以优化时间复杂度。

具体如何归并，可以参考力扣 23. 合并K个排序链表。

代码

[sol2-C++]
class Solution {
public:
    int kthSmallest(vector<vector<int>>& matrix, int k) {
        struct point {
            int val, x, y;
            point(int val, int x, int y) : val(val), x(x), y(y) {}
            bool operator> (const point& a) const { return this->val > a.val; }
        };
        priority_queue<point, vector<point>, greater<point>> que;
        int n = matrix.size();
        for (int i = 0; i < n; i++) {
            que.emplace(matrix[i][0], i, 0);
        }
        for (int i = 0; i < k - 1; i++) {
            point now = que.top();
            que.pop();
            if (now.y != n - 1) {
                que.emplace(matrix[now.x][now.y + 1], now.x, now.y + 1);
            }
        }
        return que.top().val;
    }
};

[sol2-Java]
class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] a, int[] b) {
                return a[0] - b[0];
            }
        });
        int n = matrix.length;
        for (int i = 0; i < n; i++) {
            pq.offer(new int[]{matrix[i][0], i, 0});
        }
        for (int i = 0; i < k - 1; i++) {
            int[] now = pq.poll();
            if (now[2] != n - 1) {
                pq.offer(new int[]{matrix[now[1]][now[2] + 1], now[1], now[2] + 1});
            }
        }
        return pq.poll()[0];
    }
}

[sol2-Python3]
class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix)
        pq = [(matrix[i][0], i, 0) for i in range(n)]
        heapq.heapify(pq)

        ret = 0
        for i in range(k - 1):
            num, x, y = heapq.heappop(pq)
            if y != n - 1:
                heapq.heappush(pq, (matrix[x][y + 1], x, y + 1))
        
        return heapq.heappop(pq)[0]

[sol2-Golang]
func kthSmallest(matrix [][]int, k int) int {
    h := &IHeap{}
    for i := 0; i < len(matrix); i++ {
        heap.Push(h, [3]int{matrix[i][0], i, 0})
    }

    for i := 0; i < k - 1; i++ {
        now := heap.Pop(h).([3]int)
        if now[2] != len(matrix) - 1 {
            heap.Push(h, [3]int{matrix[now[1]][now[2]+1], now[1], now[2]+1})
        }
    }
    return heap.Pop(h).([3]int)[0]
}

type IHeap [][3]int

func (h IHeap) Len() int           { return len(h) }
func (h IHeap) Less(i, j int) bool { return h[i][0] < h[j][0] }
func (h IHeap) Swap(i, j int)      { h[i], h[j] = h[j], h[i] }

func (h *IHeap) Push(x interface{}) {
	*h = append(*h, x.([3]int))
}

func (h *IHeap) Pop() interface{} {
	old := *h
	n := len(old)
	x := old[n-1]
	*h = old[0 : n-1]
	return x
}

[sol2-C]
typedef struct point {
    int val, x, y;
} point;

bool cmp(point a, point b) { return a.val >= b.val; }

void swap(point* a, point* b) {
    point t = *a;
    *a = *b, *b = t;
}

void push(point heap[], int* size, point* p) {
    heap[++(*size)] = *p;
    int s = (*size);
    while (s > 1) {
        if (cmp(heap[s], heap[s >> 1])) {
            break;
        }
        swap(&heap[s], &heap[s >> 1]);
        s >>= 1;
    }
}

void pop(point heap[], int* size) {
    heap[1] = heap[(*size)--];
    int p = 1, s = 2;
    while (s <= (*size)) {
        if (s < (*size) && !cmp(heap[s + 1], heap[s])) {
            s++;
        }
        if (cmp(heap[s], heap[p])) {
            break;
        }
        swap(&heap[s], &heap[p]);
        p = s, s = p << 1;
    }
}

int kthSmallest(int** matrix, int matrixSize, int* matrixColSize, int k) {
    point heap[matrixSize + 1];
    int size = 0;
    for (int i = 0; i < matrixSize; i++) {
        point p = {matrix[i][0], i, 0};
        push(heap, &size, &p);
    }
    for (int i = 0; i < k - 1; i++) {
        point now = heap[1];
        pop(heap, &size);
        if (now.y != matrixSize - 1) {
            point p = {matrix[now.x][now.y + 1], now.x, now.y + 1};
            push(heap, &size, &p);
        }
    }
    return heap[1].val;
}

复杂度分析

时间复杂度：$O(k\log{n})$，归并 $k$ 次，每次堆中插入和弹出的操作时间复杂度均为 $\log{n}$。
空间复杂度：$O(n)$，堆的大小始终为 $n$。

需要注意的是，$k$ 在最坏情况下是 $n^2$，因此该解法最坏时间复杂度为 $O(n^2\log{n})$。

方法三：二分查找

思路及算法

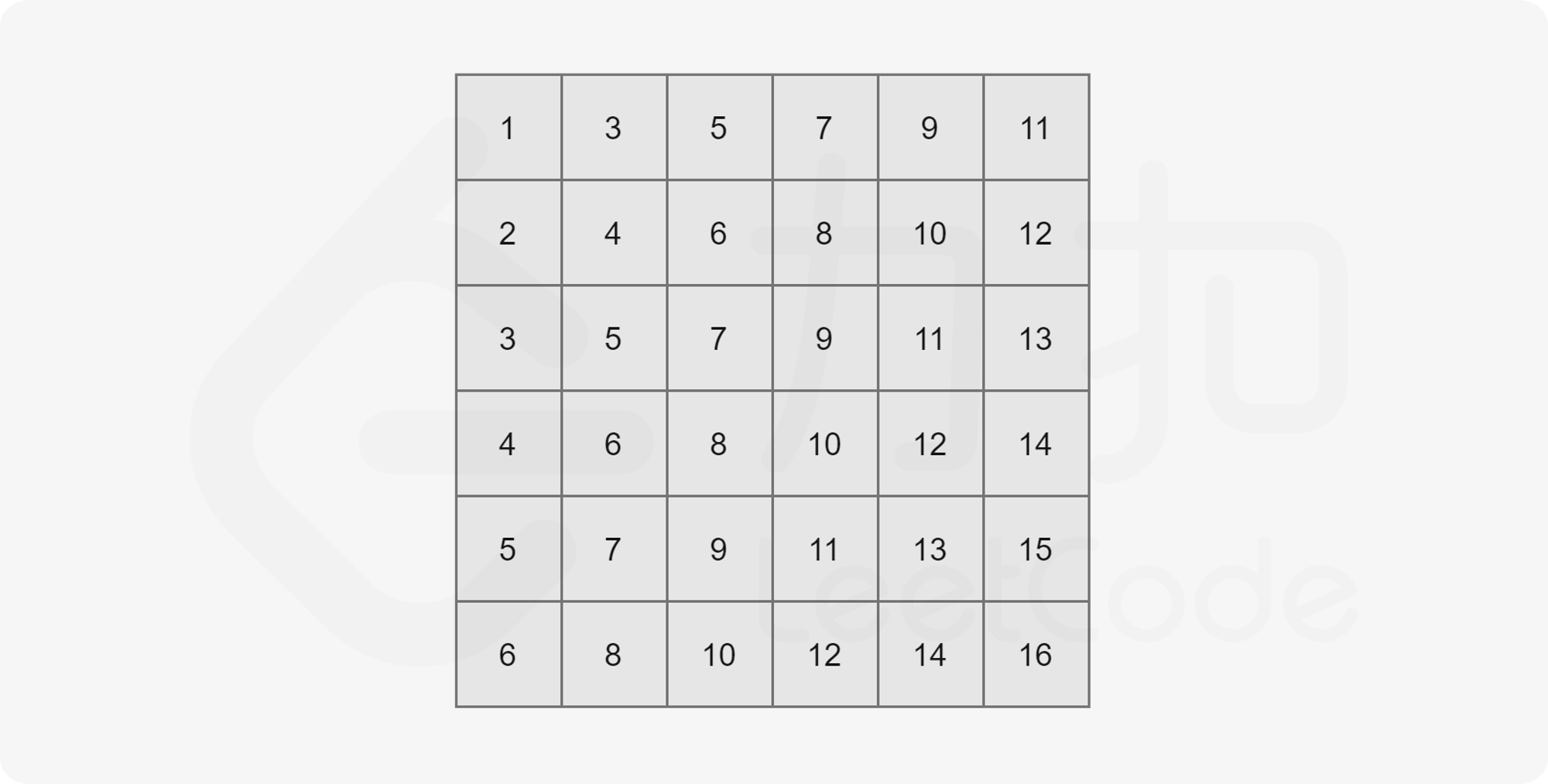
由题目给出的性质可知，这个矩阵内的元素是从左上到右下递增的（假设矩阵左上角为 $matrix[0][0]$）。以下图为例：

{:width=”80%”}

我们知道整个二维数组中 $matrix[0][0]$ 为最小值，$matrix[n - 1][n - 1]$ 为最大值，现在我们将其分别记作 $l$ 和 $r$。

可以发现一个性质：任取一个数 $mid$ 满足 $l\leq mid \leq r$，那么矩阵中不大于 $mid$ 的数，肯定全部分布在矩阵的左上角。

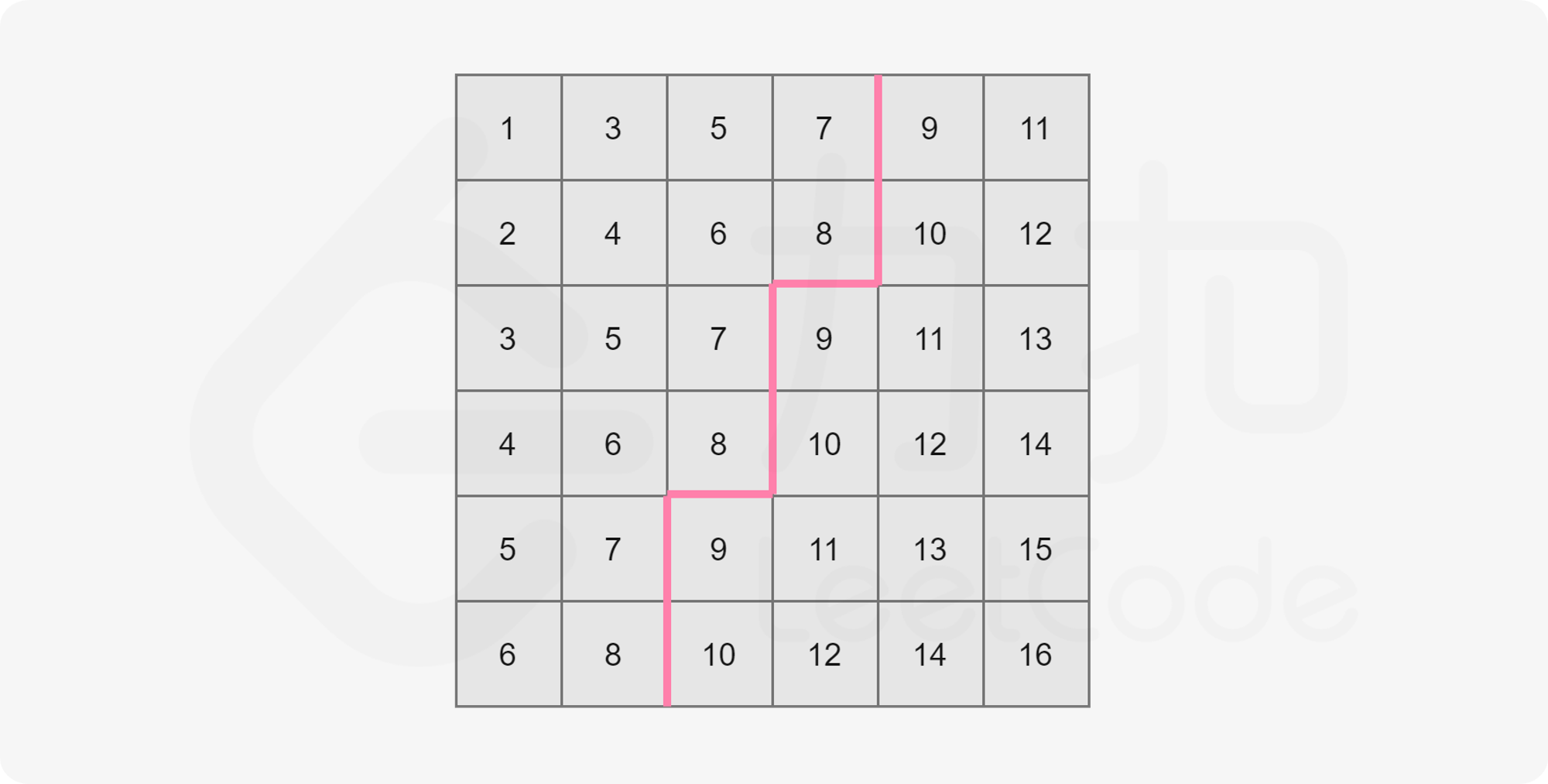
例如下图，取 $mid=8$：

{:width=”80%”}

我们可以看到，矩阵中大于 $mid$ 的数就和不大于 $mid$ 的数分别形成了两个板块，沿着一条锯齿线将这个矩形分开。其中左上角板块的大小即为矩阵中不大于 $mid$ 的数的数量。

读者也可以自己取一些 $mid$ 值，通过画图以加深理解。

我们只要沿着这条锯齿线走一遍即可计算出这两个板块的大小，也自然就统计出了这个矩阵中不大于 $mid$ 的数的个数了。

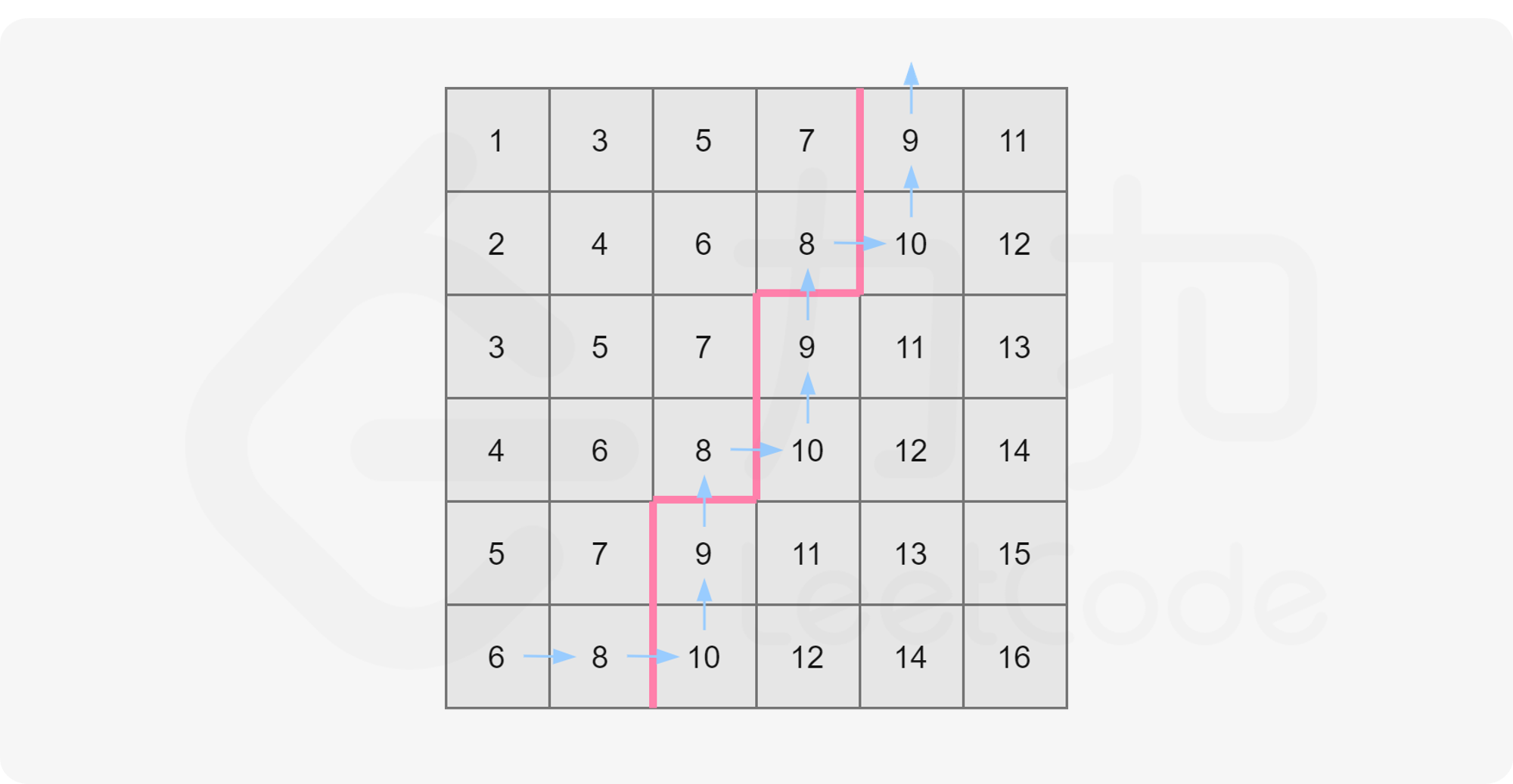
走法演示如下，依然取 $mid=8$：

{:width=”80%”}

可以这样描述走法：

初始位置在 $matrix[n - 1][0]$（即左下角）；
设当前位置为 $matrix[i][j]$。若 $matrix[i][j] \leq mid$，则将当前所在列的不大于 $mid$ 的数的数量（即 $i + 1$）累加到答案中，并向右移动，否则向上移动；
不断移动直到走出格子为止。

我们发现这样的走法时间复杂度为 $O(n)$，即我们可以线性计算对于任意一个 $mid$，矩阵中有多少数不大于它。这满足了二分查找的性质。

不妨假设答案为 $x$，那么可以知道 $l\leq x\leq r$，这样就确定了二分查找的上下界。

每次对于「猜测」的答案 $mid$，计算矩阵中有多少数不大于 $mid$ ：

如果数量不少于 $k$，那么说明最终答案 $x$ 不大于 $mid$；
如果数量少于 $k$，那么说明最终答案 $x$ 大于 $mid$。

这样我们就可以计算出最终的结果 $x$ 了。

代码

[sol3-C++]
class Solution {
public:
    bool check(vector<vector<int>>& matrix, int mid, int k, int n) {
        int i = n - 1;
        int j = 0;
        int num = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] <= mid) {
                num += i + 1;
                j++;
            } else {
                i--;
            }
        }
        return num >= k;
    }

    int kthSmallest(vector<vector<int>>& matrix, int k) {
        int n = matrix.size();
        int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (check(matrix, mid, k, n)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }
};

[sol3-Java]
class Solution {
    public int kthSmallest(int[][] matrix, int k) {
        int n = matrix.length;
        int left = matrix[0][0];
        int right = matrix[n - 1][n - 1];
        while (left < right) {
            int mid = left + ((right - left) >> 1);
            if (check(matrix, mid, k, n)) {
                right = mid;
            } else {
                left = mid + 1;
            }
        }
        return left;
    }

    public boolean check(int[][] matrix, int mid, int k, int n) {
        int i = n - 1;
        int j = 0;
        int num = 0;
        while (i >= 0 && j < n) {
            if (matrix[i][j] <= mid) {
                num += i + 1;
                j++;
            } else {
                i--;
            }
        }
        return num >= k;
    }
}

[sol3-Python3]
class Solution:
    def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
        n = len(matrix)

        def check(mid):
            i, j = n - 1, 0
            num = 0
            while i >= 0 and j < n:
                if matrix[i][j] <= mid:
                    num += i + 1
                    j += 1
                else:
                    i -= 1
            return num >= k

        left, right = matrix[0][0], matrix[-1][-1]
        while left < right:
            mid = (left + right) // 2
            if check(mid):
                right = mid
            else:
                left = mid + 1
        
        return left

[sol3-Golang]
func kthSmallest(matrix [][]int, k int) int {
    n := len(matrix)
    left, right := matrix[0][0], matrix[n-1][n-1]
    for left < right {
        mid := left + (right - left) / 2
        if check(matrix, mid, k, n) {
            right = mid
        } else {
            left = mid + 1
        }
    }
    return left
}

func check(matrix [][]int, mid, k, n int) bool {
    i, j := n - 1, 0
    num := 0
    for i >= 0 && j < n {
        if matrix[i][j] <= mid {
            num += i + 1
            j++
        } else {
            i--
        }
    }
    return num >= k
}

[sol3-C]
bool check(int **matrix, int mid, int k, int n) {
    int i = n - 1;
    int j = 0;
    int num = 0;
    while (i >= 0 && j < n) {
        if (matrix[i][j] <= mid) {
            num += i + 1;
            j++;
        } else {
            i--;
        }
    }
    return num >= k;
}

int kthSmallest(int **matrix, int matrixSize, int *matrixColSize, int k) {
    int left = matrix[0][0];
    int right = matrix[matrixSize - 1][matrixSize - 1];
    while (left < right) {
        int mid = left + ((right - left) >> 1);
        if (check(matrix, mid, k, matrixSize)) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}

复杂度分析

时间复杂度：$O(n\log(r-l))$，二分查找进行次数为 $O(\log(r-l))$，每次操作时间复杂度为 $O(n)$。
空间复杂度：$O(1)$。

写在最后

上述三种解法，第一种没有利用矩阵的性质，所以时间复杂度最差；第二种解法只利用了一部分性质（每一行是一个有序数列，而忽视了列之间的关系）；第三种解法则利用了全部性质，所以时间复杂度最佳。

这也启示我们要认真把握题目中的条件与性质，更有利于我们解题。

统计信息

通过次数	提交次数	AC比率
83440	130532	63.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
查找和最小的K对数字	中等
乘法表中第k小的数	困难
找出第 k 小的距离对	困难
第 K 个最小的素数分数	困难

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途

英文原文

中文题目

通过代码

高赞题解

方法一：直接排序

方法二：归并排序

方法三：二分查找

写在最后

统计信息

提交历史

相似题目

你的赏识是我前进的动力