原文链接: https://leetcode-cn.com/problems/random-point-in-non-overlapping-rectangles

英文原文

You are given an array of non-overlapping axis-aligned rectangles rects where rects[i] = [ai, bi, xi, yi] indicates that (ai, bi) is the bottom-left corner point of the ith rectangle and (xi, yi) is the top-right corner point of the ith rectangle. Design an algorithm to pick a random integer point inside the space covered by one of the given rectangles. A point on the perimeter of a rectangle is included in the space covered by the rectangle.

Any integer point inside the space covered by one of the given rectangles should be equally likely to be returned.

Note that an integer point is a point that has integer coordinates.

Implement the Solution class:

• Solution(int[][] rects) Initializes the object with the given rectangles rects.
• int[] pick() Returns a random integer point [u, v] inside the space covered by one of the given rectangles.

 

Example 1:

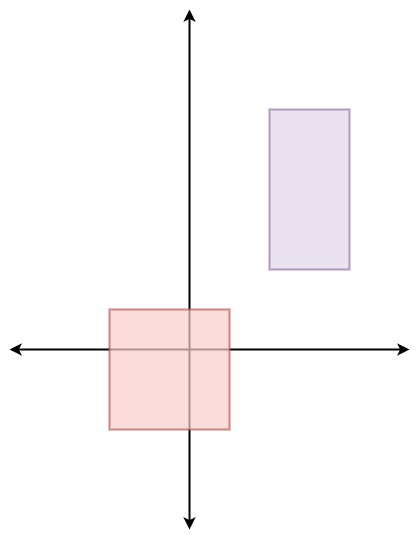
Input
["Solution", "pick", "pick", "pick", "pick", "pick"]
[[[[-2, -2, 1, 1], [2, 2, 4, 6]]], [], [], [], [], []]
Output
[null, [1, -2], [1, -1], [-1, -2], [-2, -2], [0, 0]]

Explanation
Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
solution.pick(); // return [1, -2]
solution.pick(); // return [1, -1]
solution.pick(); // return [-1, -2]
solution.pick(); // return [-2, -2]
solution.pick(); // return [0, 0]

 

Constraints:

• 1 <= rects.length <= 100
• rects[i].length == 4
• -109 <= ai < xi <= 109
• -109 <= bi < yi <= 109
• xi - ai <= 2000
• yi - bi <= 2000
• All the rectangles do not overlap.
• At most 104 calls will be made to pick.

中文题目

给定一个非重叠轴对齐矩形的列表 rects，写一个函数 pick 随机均匀地选取矩形覆盖的空间中的整数点。

提示：

1. 整数点是具有整数坐标的点。
2. 矩形周边上的点包含在矩形覆盖的空间中。
3. 第 i 个矩形 rects [i] = [x1，y1，x2，y2]，其中 [x1，y1] 是左下角的整数坐标，[x2，y2] 是右上角的整数坐标。
4. 每个矩形的长度和宽度不超过 2000。
5. 1 <= rects.length <= 100
6. pick 以整数坐标数组 [p_x, p_y] 的形式返回一个点。
7. pick 最多被调用10000次。

 

示例 1：

输入: 
["Solution","pick","pick","pick"]
[[[[1,1,5,5]]],[],[],[]]
输出: 
[null,[4,1],[4,1],[3,3]]

示例 2：

输入: 
["Solution","pick","pick","pick","pick","pick"]
[[[[-2,-2,-1,-1],[1,0,3,0]]],[],[],[],[],[]]
输出: 
[null,[-1,-2],[2,0],[-2,-1],[3,0],[-2,-2]]

 

输入语法的说明：

输入是两个列表：调用的子例程及其参数。Solution 的构造函数有一个参数，即矩形数组 rects。pick 没有参数。参数总是用列表包装的，即使没有也是如此。

 

通过代码

官方题解

方法一：二分查找

我们用 w[i] 表示第 i 个矩形 rect[i] 中整数点的数目，那么我们的随机算法需要使得每个矩形被选到的概率与 w[i] 成正比（这样也就保证了空间中的每个整数点被选到的概率都是相等的）。具体地，rect[i] 被选到的概率应当为 w[i] / sum(w[i])，其中 sum(w[i]) 表示空间中的整数点数目之和。

令 tot = sum(w[i])，我们可以在 [0, tot) 区间内生成随机整数。假设生成的数为 x，那么我们需要找到满足 prefix(w[i - 1]) <= x < prefix(w[i]) 的 i，其中 prefix(w[i]) 表示前 i 个矩形中整数点的数目之和，此时我们选中了第 i 个矩形。我们可以使用二分查找，找出对应的 i。

在选中了第 i 个矩形后，我们也可以在 [0, w[i]) 中再次生成随机数，来在这个矩形中随机选择一个点。更好的做法是我们仍然使用之前生成的数 x，令 y = x - prefix(w[i - 1])，我们只需要选择第 i 个矩形中的第 y 个点即可，对应的坐标为：

x_coord = x_start + y % (x_end - x_start + 1)
y_coord = y_start + y / (x_end - x_start + 1)

这相当于把第 i 个矩形中的坐标按照 y 轴优先的顺序依次排列，每一个点都可以通过上述的方式恢复到矩形中的坐标。

{:width=260px}

[sol1]
class Solution {
public:

    vector<vector<int>> rects;
    vector<int> psum;
    int tot = 0;
    //c++11 random integer generation
    mt19937 rng{random_device{}()};
    uniform_int_distribution<int> uni;

    Solution(vector<vector<int>> rects) {
        this->rects = rects;
        for (auto& x : rects) {
            tot += (x[2] - x[0] + 1) * (x[3] - x[1] + 1);
            psum.push_back(tot);
        }
        uni = uniform_int_distribution<int>{0, tot - 1};
    }

    vector<int> pick() {
        int targ = uni(rng);

        int lo = 0;
        int hi = rects.size() - 1;
        while (lo != hi) {
            int mid = (lo + hi) / 2;
            if (targ >= psum[mid]) lo = mid + 1;
            else hi = mid;
        }

        auto& x = rects[lo];
        int width = x[2] - x[0] + 1;
        int height = x[3] - x[1] + 1;
        int base = psum[lo] - width * height;
        return {x[0] + (targ - base) % width, x[1] + (targ - base) / width};
    }
};

[sol1]
class Solution {

    int[][] rects;
    List<Integer> psum = new ArrayList<>();
    int tot = 0;
    Random rand = new Random();

    public Solution(int[][] rects) {
        this.rects = rects;
        for (int[] x : rects){
            tot += (x[2] - x[0] + 1) * (x[3] - x[1] + 1);
            psum.add(tot);
        }
    }

    public int[] pick() {
        int targ = rand.nextInt(tot);

        int lo = 0;
        int hi = rects.length - 1;
        while (lo != hi) {
            int mid = (lo + hi) / 2;
            if (targ >= psum.get(mid)) lo = mid + 1;
            else hi = mid;
        }

        int[] x = rects[lo];
        int width = x[2] - x[0] + 1;
        int height = x[3] - x[1] + 1;
        int base = psum.get(lo) - width * height;
        return new int[]{x[0] + (targ - base) % width, x[1] + (targ - base) / width};
    }
}

复杂度分析

• 时间复杂度：预处理的时间复杂度为 $O(N)$，随机选取的单次时间复杂度为 $O(\log N)$。

• 空间复杂度：$O(N)$。

统计信息

通过次数	提交次数	AC比率
3228	7989	40.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
按权重随机选择	中等
在圆内随机生成点	中等