原文链接: https://leetcode-cn.com/problems/find-largest-value-in-each-tree-row

英文原文

Given the root of a binary tree, return an array of the largest value in each row of the tree (0-indexed).

 

 

Example 1:

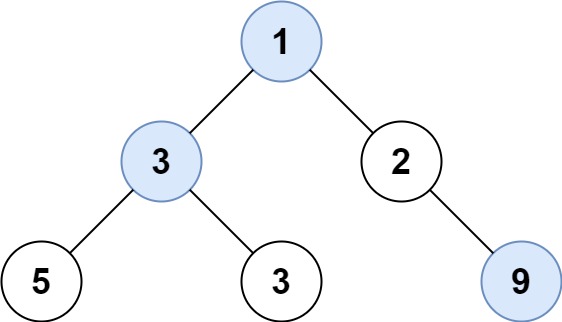
Input: root = [1,3,2,5,3,null,9]
Output: [1,3,9]

Example 2:

Input: root = [1,2,3]
Output: [1,3]

Example 3:

Input: root = [1]
Output: [1]

Example 4:

Input: root = [1,null,2]
Output: [1,2]

Example 5:

Input: root = []
Output: []

 

Constraints:

• The number of nodes in the tree will be in the range [0, 104].
• -231 <= Node.val <= 231 - 1

中文题目

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。

 

示例1：

输入: root = [1,3,2,5,3,null,9]
输出: [1,3,9]
解释:
          1
         / \
        3   2
       / \   \  
      5   3   9 

示例2：

输入: root = [1,2,3]
输出: [1,3]
解释:
          1
         / \
        2   3

示例3：

输入: root = [1]
输出: [1]

示例4：

输入: root = [1,null,2]
输出: [1,2]
解释:      
           1 
            \
             2     

示例5：

输入: root = []
输出: []

 

提示：

• 二叉树的节点个数的范围是 [0,104]
• -231 <= Node.val <= 231 - 1

通过代码

高赞题解

一，首先是BFS，这个比较简单，就是一行一行的遍历，像下面图中这样，在每一行中找到最大值即可

public List<Integer> largestValues(TreeNode root) {
    //LinkedList实现队列
    Queue<TreeNode> queue = new LinkedList<>();
    List<Integer> values = new ArrayList<>();
    if (root != null)
        queue.add(root);//入队
    while (!queue.isEmpty()) {
        int max = Integer.MIN_VALUE;
        int levelSize = queue.size();//每一层的数量
        for (int i = 0; i < levelSize; i++) {
            TreeNode node = queue.poll();//出队
            max = Math.max(max, node.val);//记录每层的最大值
            if (node.left != null)
                queue.add(node.left);
            if (node.right != null)
                queue.add(node.right);
        }
        values.add(max);
    }
    return values;
}

二，DFS解决
除了一层一层遍历以外，我们还可以使用DFS（深度优先搜索算法）来求解。我们就以上面的举例来画个图分析一下

public List<Integer> largestValues(TreeNode root) {
    List<Integer> res = new ArrayList<>();
    helper(root, res, 1);
    return res;
}

//level表示的是第几层，集合res中的第一个数据表示的是
// 第一层的最大值，第二个数据表示的是第二层的最大值……
private void helper(TreeNode root, List<Integer> res, int level) {
    if (root == null)
        return;
    //如果走到下一层了直接加入到集合中
    if (level == res.size() + 1) {
        res.add(root.val);
    } else {
        //注意：我们的level是从1开始的，也就是说root
        // 是第一层，而集合list的下标是从0开始的，
        // 所以这里level要减1。
        // Math.max(res.get(level - 1), root.val)表示的
        // 是遍历到的第level层的root.val值和集合中的第level
        // 个元素的值哪个大，就要哪个。
        res.set(level - 1, Math.max(res.get(level - 1), root.val));
    }
    //下面两行是DFS的核心代码
    helper(root.left, res, level + 1);
    helper(root.right, res, level + 1);
}

查看更多答案，可关注我微信公众号“**数据结构和算法**”，也可以扫描上方二维码关注

统计信息

通过次数	提交次数	AC比率
43050	66565	64.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言