538-把二叉搜索树转换为累加树(Convert BST to Greater Tree)
发表于：2021-12-03 | 分类： 中等
字数统计: 2.4k | 阅读时长: 12分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/convert-bst-to-greater-tree

英文原文

Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.

As a reminder, a binary search tree is a tree that satisfies these constraints:

  • The left subtree of a node contains only nodes with keys less than the node's key.
  • The right subtree of a node contains only nodes with keys greater than the node's key.
  • Both the left and right subtrees must also be binary search trees.

 

Example 1:

Input: root = [4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
Output: [30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

Example 2:

Input: root = [0,null,1]
Output: [1,null,1]

Example 3:

Input: root = [1,0,2]
Output: [3,3,2]

Example 4:

Input: root = [3,2,4,1]
Output: [7,9,4,10]

 

Constraints:

  • The number of nodes in the tree is in the range [0, 104].
  • -104 <= Node.val <= 104
  • All the values in the tree are unique.
  • root is guaranteed to be a valid binary search tree.

 

Note: This question is the same as 1038: https://leetcode.com/problems/binary-search-tree-to-greater-sum-tree/

中文题目

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

  • 节点的左子树仅包含键 小于 节点键的节点。
  • 节点的右子树仅包含键 大于 节点键的节点。
  • 左右子树也必须是二叉搜索树。

注意：本题和 1038: https://leetcode-cn.com/problems/binary-search-tree-to-greater-sum-tree/ 相同

 

示例 1：

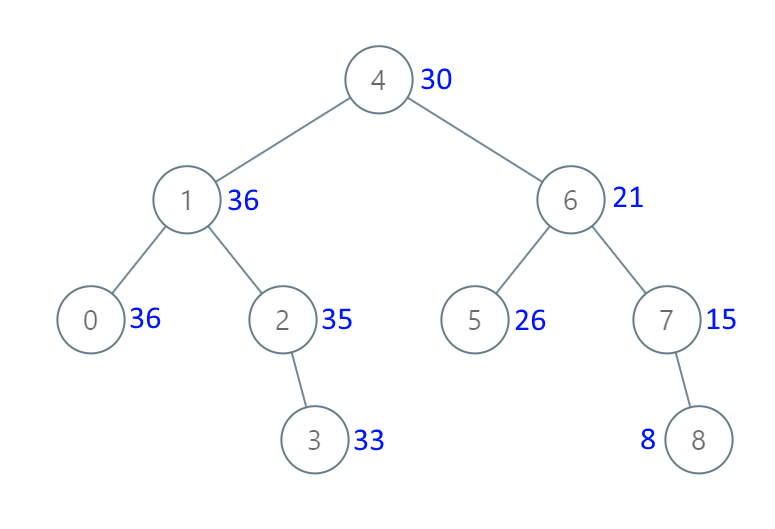
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

 

提示：

  • 树中的节点数介于 0 和 104 之间。
  • 每个节点的值介于 -104 和 104 之间。
  • 树中的所有值 互不相同 。
  • 给定的树为二叉搜索树。

通过代码

高赞题解

本文将带你用树的一种遍历算法解决N个leetcode相关算法题(算法小渣渣致敬叶师傅)

我不害怕曾經練過一萬種踢法的人，但我害怕一種踢法練過一萬次的人(by 叶师傅的徒弟Bruce Lee)

树的遍历(Traversal)

如下图, 三种遍历方式, 可用同一种递归思想实现

先序遍历(PreOrder, 按照先访问根节点的顺序)

var preorderTraversal = function(root) {
  const res = []
  function traversal (root) {
    if (root !== null) {
      res.push(root.val) // 访问根节点的值
      traversal(root.left) // 递归遍历左子树
      traversal(root.right) // 递归遍历右子树
    }
  }
  traversal(root)
  return res
}

94 中序遍历(InOrder, 按照根节点在中间访问的顺序)

var inorderTraversal = function(root) {
  const res = []
  function traversal (root) {
    if (root !== null) {
      traversal(root.left)
      res.push(root.val)
      traversal(root.right)
    }
  }
  traversal(root)
  return res
}

145 后续遍历(PosterOrder, 按照根节点在后面访问的顺序)

var postorderTraversal = function(root) {
  const res = []
  function traversal (root) {
    if (root !== null) {
      traversal(root.left)
      traversal(root.right)
      res.push(root.val)
    }
  }
  traversal(root)
  return res
}

100 相同的树

可以利用这种递归思想并发同时爬两棵树

var isSameTree = function(p, q) {
  function traversal (root1, root2) {
    if (root1 === null && root2 !== null) {
      return false
    } else if (root1 !== null && root2 === null) {
      return false
    } else if (root1 === null && root2 === null) {
      return true
    } else {
      return  root1.val === root2.val && traversal(root1.left, root2.left) && traversal(root1.right, root2.right)
    }
  }
  return traversal(p, q)
}

226 翻转二叉树

这种算法可以帮助Homebrew作者Max Howell解开Google的算法面试题

var invertTree = function(root) {
  function traversal (root) {
    if (root === null) {
      return null
    } else {
      [root.left, root.right] = [traversal(root.right), traversal(root.left)]
      return root
    }
  }
  return  traversal(root)
}

590 N叉树的后序遍历

我们还可以用此种算法解决N叉树的问题

var postorder = function(root) {
  const res = []
  function traversal (root) {
    if (root !== null) {
      root.children.forEach(child => {
        traversal(child)
      })
      res.push(root.val)
    }
  }
  traversal(root)
  return res
}

如果你已对这种写法审美疲劳, 可以换个写法, 使用匿名函数

var postorder = function(root) {
  const res = []
  ;(function (root) {
    if (root !== null) {
      root.children.forEach(child => {
        arguments.callee(child)
      })
      res.push(root.val)
    }
  })(root)
  return res
}

还可以利用栈来迭代

var postorder = function(root) {
  if (root === null) {
    return []
  }
  const res = []
  const arr = [root]
  while (arr.length) {
    const cur = arr.pop()
    res.push(cur.val)
    for (let i = cur.children.length - 1; i >= 0; i--) {
      arr.push(cur.children[i])
    }
  }
  return res.reverse()
}

103 二叉树的锯齿形层次遍历

大白话, 蛇皮走位爬树

var zigzagLevelOrder = function(root) {
  if (root === null) {
    return []
  } else {
    let res = []
    function traversal (root, depth) {
      if (root !== null) {
        if (res[depth] === undefined) {
          res[depth] = []
        }
        res[depth].push(root.val)
        traversal(root.left, depth + 1)
        traversal(root.right, depth + 1)
      }
    }
    traversal(root, 0)
    res.forEach((item, index) => {
      if (index & 1) {
        res[index] = item.reverse()
      }
    })
    return res
  }
}

优化

var zigzagLevelOrder = function(root) {
  if (root === null) {
    return []
  } else {
    let res = []
    function traversal (root, depth) {
      if (root !== null) {
        if (res[depth] === undefined) {
          res[depth] = []
        }
        if (depth & 1) {
          res[depth].unshift(root.val)
        } else {
          res[depth].push(root.val)
        }
        traversal(root.left, depth + 1)
        traversal(root.right, depth + 1)
      }
    }
    traversal(root, 0)
    return res
  }
}

230 二叉搜索树中第K小的元素

var kthSmallest = function (root, k) {
  let arr = []
  function traversal (node) {
    if (node !== null) {
      traversal(node.left)
      arr.push(node.val)
      traversal(node.right)
    }
  }
  traversal(root)
  return arr[k - 1]
}

优化, 减少遍历次数

var kthSmallest = function (root, k) {
  let arr = []
  function traversal(node) {
    if (node !== null && arr.length < k) {
      traversal(node.left)
      arr.push(node.val)
      traversal(node.right)
    }
  }
  traversal(root)
  return arr[k - 1]
}

进一步优化, 使用O(1)的额外空间

var kthSmallest = function (root, k) {
  let res
  let count = 0
  function traversal(node) {
    if (node !== null) {
      if (count < k) {
        traversal(node.left)
      }
      if (++count === k) {
        res = node.val
      }
      if (count < k) {
        traversal(node.right)
      }
    }
  }
  traversal(root)
  return res
}

102 二叉树的层序遍历

var levelOrder = function(root) {
  const res = []
  function traversal (root, depth) {
    if (root !== null) {
      if (!res[depth]) {
        res[depth] = []
      }
      traversal(root.left, depth + 1)
      res[depth].push(root.val)
      traversal(root.right, depth + 1)
    }
  }
  traversal(root, 0)
  return res
}

199 二叉树的右视图

基本思路: 先序遍历, 记录每一层深度下的节点的值, 并先记录左节点再记录右节点, 则最后记录的值即为该层深度的右视图看到的值

var rightSideView = function(root) {
  const arr = []
  function traversal (root, depth) {
    if (root) {
      if (arr[depth] === undefined) {
        arr[depth] = []
      }
      arr[depth].push(root.val)
      traversal(root.left, depth + 1)
      traversal(root.right, depth + 1)
    }
  }
  traversal(root, 0)
  const res = []
  for (let i = 0; i < arr.length; ++i) {
    res.push(arr[i][arr[i].length - 1])
  }
  return res
};

104 二叉树的最大深度

var maxDepth = function (root) {
  let res = 0
  function traversal (root, depth) {
    if (root !== null) {
      if (depth > res) {
        res = depth
      }
      if (root.left) {
        traversal(root.left, depth + 1)
      }
      if (root.right) {
        traversal(root.right, depth + 1)
      }
    }
  }
  traversal(root, 1)
  return res
}

107 二叉树的层次遍历 II

var levelOrderBottom = function(root) {
  if (root === null) {
    return []
  }
  let res = []
  function traversal (root, depth) {
    if (root !== null) {
      if (!res[depth]) {
        res[depth] = []
      }
      traversal(root.left, depth + 1)
      res[depth].push(root.val)
      traversal(root.right, depth + 1)
    }
  }
  traversal(root, 0)
  return res.reverse()
}

671 二叉树中第二小的节点

var findSecondMinimumValue = function(root) {
  let arr = []
  ;(function traversal (root) {
    if (root !== null) {
      traversal(root.left)
      arr.push(root.val)
      traversal(root.right)
    }
  })(root)
  let _arr = [...new Set(arr)].sort()
  return _arr[1] ? _arr[1] : -1
}

1038 从二叉搜索树到更大和树

var bstToGst = function(root) {
  let sum = 0
  function traversal (root) {
    if (root !== null) {
      traversal(root.right)
      root.val += sum
      sum = root.val
      traversal(root.left)
    }
  }
  traversal(root)
  return root
}

538 把二叉搜索树转换为累加树

var convertBST = function(root) {
  let sum = 0
  function traversal (root) {
    if (root !== null) {
      traversal(root.right)
      sum += root.val
      root.val = sum
      traversal(root.left)
    }
  }
  traversal(root)
  return root
}

700 二叉搜索树中的搜索

var searchBST = function(root, val) {
  function traversal (root) {
    if (root !== null) {
      if (root.val === val) {
        return root
      } else if (root.val < val) {
        return traversal(root.right)
      } else {
        return traversal(root.left)
      }
    } else {
      return root
    }
  }
  return traversal(root)
}

559 N叉树的最大深度

var maxDepth = function(root) {
  if (root === null) {
    return 0
  } else {
    let depth = 1
    function traversal (root, curDepth) {
      if (root !== null) {
        if (curDepth > depth) {
          depth = curDepth
        }
        root.children.forEach(child => traversal(child, curDepth + 1))
      }
    }
    traversal(root, 1)
    return depth
  }
}

589 N叉树的前序遍历

var preorder = function(root) {
  const res = []
  function traversal (root) {
    if (root !== null) {
      res.push(root.val)
      root.children.forEach(child => traversal(child))
    }
  }
  traversal(root)
  return res
}

897 递增顺序查找树

var increasingBST = function(root) {
  const arr = []
  function traversal (root) {
    if (root !== null) {
      traversal(root.left)
      arr.push(root.val)
      traversal(root.right)
    }
  }
  traversal(root)
  const res = new TreeNode(arr[0])
  let currentNode = res
  for (let i = 0; i < arr.length - 1; i++) {
    currentNode.left = null
    currentNode.right = new TreeNode(arr[i + 1])
    currentNode = currentNode.right
  }
  return res
}

原文在掘金: https://juejin.im/post/5e1c4e46f265da3e140fa54d

欢迎点赞👍、关注和来撩三连😎

统计信息

通过次数 提交次数 AC比率
117140 165442 70.8%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
深度优先搜索 树 二叉树 二叉搜索树
上一篇:
537-复数乘法(Complex Number Multiplication)
下一篇:
539-最小时间差(Minimum Time Difference)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo