542-01 矩阵(01 Matrix) | 凤起丶宛南

原文链接: https://leetcode-cn.com/problems/01-matrix

英文原文

Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.

The distance between two adjacent cells is 1.

Example 1:

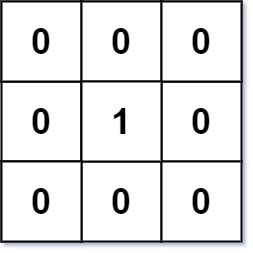
Input: mat = [[0,0,0],[0,1,0],[0,0,0]]
Output: [[0,0,0],[0,1,0],[0,0,0]]

Example 2:

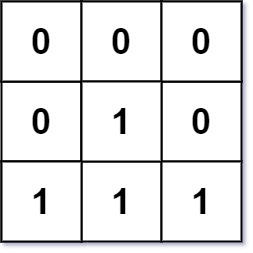
Input: mat = [[0,0,0],[0,1,0],[1,1,1]]
Output: [[0,0,0],[0,1,0],[1,2,1]]

Constraints:

m == mat.length
n == mat[i].length
1 <= m, n <= 10⁴
1 <= m * n <= 10⁴
mat[i][j] is either 0 or 1.
There is at least one 0 in mat.

中文题目

给定一个由 0 和 1 组成的矩阵 mat ，请输出一个大小相同的矩阵，其中每一个格子是 mat 中对应位置元素到最近的 0 的距离。

两个相邻元素间的距离为 1 。

示例 1：

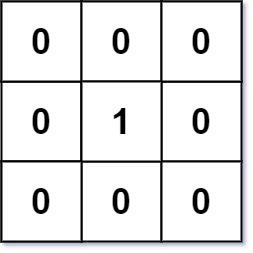
输入：mat = [[0,0,0],[0,1,0],[0,0,0]]
输出：[[0,0,0],[0,1,0],[0,0,0]]

示例 2：

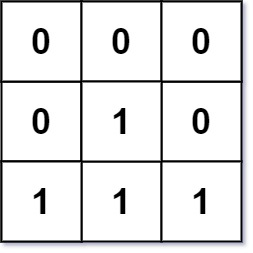
输入：mat = [[0,0,0],[0,1,0],[1,1,1]]
输出：[[0,0,0],[0,1,0],[1,2,1]]

提示：

m == mat.length
n == mat[i].length
1 <= m, n <= 10⁴
1 <= m * n <= 10⁴
mat[i][j] is either 0 or 1.
mat 中至少有一个 0

通过代码

高赞题解

🙋今日份打卡~

这道题和前几天的打卡题「1162.地图分析」一毛一样！那道题是可以理解为需要找到每个 $0$ 最近的 $1$，而今天这道题是找每个 $1$ 最近的 $0$。

这里斗胆模仿一下前额叶 dalao 的文风就是 「吃🐳！秒懂多源 BFS 看上面这 1 篇就够了！还送 D 版 pdf！👏」

一、广度优先搜索

思路：

对于 「Tree 的 BFS」（典型的「单源 BFS」） 大家都已经轻车熟路了：
- 首先把 root 节点入队，再一层一层无脑遍历就行了。
对于 「图的 BFS」（「多源 BFS」） 做法其实也是一样滴～，与「Tree 的 BFS」的区别注意以下两条就 ok 辣～
- Tree 只有 1 个 root，而图可以有多个源点，所以首先需要把多个源点都入队；
- Tree 是有向的因此不需要标识是否访问过，而对于无向图来说，必须得标志是否访问过哦！并且为了防止某个节点多次入队，需要在其入队之前就将其设置成已访问！【看见很多人说自己的 BFS 超时了，坑就在这里哈哈哈

做法：

根据上述思路，本题怎么做就很简单了：

首先把每个源点 $0$ 入队，然后从各个 $0$ 同时开始一圈一圈的向 $1$ 扩散（每个 $1$ 都是被离它最近的 $0$ 扩散到的），扩散的时候可以设置 int[][] dist 来记录距离（即扩散的层次）并同时标志是否访问过。对于本题是可以直接修改原数组 int[][] matrix 来记录距离和标志是否访问的，这里要注意先把 matrix 数组中 1 的位置设置成 -1 （设成Integer.MAX_VALUE啦，m * n啦，10000啦都行，只要是个无效的距离值来标志这个位置的 1 没有被访问过就行辣~）

复杂度分析：

每个点入队出队一次，所以时间复杂度：$O(n * m)$
虽然我们是直接原地修改的原输入数组来存储结果，但最差的情况下即全都是 $0$ 时，需要把 $m * n$ 个 $0$ 都入队，因此空间复杂度是 $O(n * m)$

[]
class Solution {
    public int[][] updateMatrix(int[][] matrix) {
        // 首先将所有的 0 都入队，并且将 1 的位置设置成 -1，表示该位置是 未被访问过的 1
        Queue<int[]> queue = new LinkedList<>();
        int m = matrix.length, n = matrix[0].length;
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    queue.offer(new int[] {i, j});
                } else {
                    matrix[i][j] = -1;
                } 
            }
        }
        
        int[] dx = new int[] {-1, 1, 0, 0};
        int[] dy = new int[] {0, 0, -1, 1};
        while (!queue.isEmpty()) {
            int[] point = queue.poll();
            int x = point[0], y = point[1];
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i];
                int newY = y + dy[i];
                // 如果四邻域的点是 -1，表示这个点是未被访问过的 1
                // 所以这个点到 0 的距离就可以更新成 matrix[x][y] + 1。
                if (newX >= 0 && newX < m && newY >= 0 && newY < n 
                        && matrix[newX][newY] == -1) {
                    matrix[newX][newY] = matrix[x][y] + 1;
                    queue.offer(new int[] {newX, newY});
                }
            }
        }

        return matrix;
    }
}

另一种 BFS 思路：

本题还有一种 BFS 的做法，就是先找出在 $0$ 边上的所有的 $1$，然后把这些 $1$ 放到队列里，后续BFS的时候就只关心 $1$ 的值。
直接看注释叭～～

[]
class Solution {
    public int[][] updateMatrix(int[][] matrix) {
        // 首先将 0 边上的 1 入队
        int[] dx = new int[] {-1, 1, 0, 0};
        int[] dy = new int[] {0, 0, -1, 1};
        Queue<int[]> queue = new LinkedList<>();
        int m = matrix.length, n = matrix[0].length;
        int[][] res = new int[m][n];
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == 0) {
                    for (int k = 0; k < 4; k++) {
                        int x = i + dx[k];
                        int y = j + dy[k];
                        if (x >= 0 && x < m && y >= 0 && y < n 
                                && matrix[x][y] == 1 && res[x][y] == 0) {
                            // 这是在 0 边上的1。需要加上 res[x][y] == 0 的判断防止重复入队
                            res[x][y] = 1;
                            queue.offer(new int[] {x, y});
                        }
                    }
                }
            }
        }

        while (!queue.isEmpty()) {
            int[] point = queue.poll();
            int x = point[0], y = point[1];
            for (int i = 0; i < 4; i++) {
                int newX = x + dx[i];
                int newY = y + dy[i];
                if (newX >= 0 && newX < m && newY >= 0 && newY < n 
                        && matrix[newX][newY] == 1 && res[newX][newY] == 0) {
                    res[newX][newY] = res[x][y] + 1;
                    queue.offer(new int[] {newX, newY});
                }
            }
        }

        return res;
    }
}

二、动态规划

对于任一点 $(i, j)$，距离 $0$ 的距离为：
$$
f(i, j) = \begin{cases}
1 + min(f(i-1, j), f(i, j-1), f(i+1, j), f(i, j+1)) & \text{if matrix[i][j] == 1} \
0 & \text{if matrix[i][j] == 0}
\end{cases}
$$

因此我们用 $dp[i][j]$ 来表示该位置距离最近的 $0$ 的距离。
我们发现 $dp[i][j]$ 是由其上下左右四个状态来决定，无法从一个方向开始递推！

于是我们尝试将问题分解：

距离 $(i, j)$ 最近的 $0$ 的位置，是在其「左上，右上，左下，右下」4个方向之一；
因此我们分别从四个角开始递推，就分别得到了位于「左上方、右上方、左下方、右下方」距离 $(i, j)$ 的最近的 $0$ 的距离，取 $min$ 即可；
通过上两步思路，我们可以很容易的写出 $4$ 个双重 $for$ 循环，动态规划的解法写到这一步其实已经完全 $OK$ 了；

如果第三步还不满足的话，从四个角开始的 $4$ 次递推，其实还可以优化成从任一组对角开始的 $2$ 次递推，比如只写从左上角、右下角开始递推就行了，为啥这样可以呢？且听我不负责任的草率论证 = = #

首先从左上角开始递推 $dp[i][j]$ 是由其「左方」和「左上方」的最优子状态决定的；
然后从右下角开始递推 $dp[i][j]$ 是由其「右方」和「右下方」的最优子状态决定的；
看起来第一次递推的时候，把「右上方」的最优子状态给漏掉了，其实不是的，因为第二次递推的时候「右方」的状态在第一次递推时已经包含了「右上方」的最优子状态了；

看起来第二次递推的时候，把「左下方」的最优子状态给漏掉了，其实不是的，因为第二次递推的时候「右下方」的状态在第一次递推时已经包含了「左下方」的最优子状态了。

[]
class Solution {
  public int[][] updateMatrix(int[][] matrix) {
    int m = matrix.length, n = matrix[0].length;
    int[][] dp = new int[m][n];
    for (int i = 0; i < m; i++) {
      for (int j = 0; j < n; j++) {
        dp[i][j] = matrix[i][j] == 0 ? 0 : 10000;
      }
    }

    // 从左上角开始
    for (int i = 0; i < m; i++) {
      for (int j = 0; j < n; j++) {
        if (i - 1 >= 0) {
          dp[i][j] = Math.min(dp[i][j], dp[i - 1][j] + 1);
        }
        if (j - 1 >= 0) {
          dp[i][j] = Math.min(dp[i][j], dp[i][j - 1] + 1);
        }
      }
    }
    // 从右下角开始
    for (int i = m - 1; i >= 0; i--) {
      for (int j = n - 1; j >= 0; j--) {
        if (i + 1 < m) {
          dp[i][j] = Math.min(dp[i][j], dp[i + 1][j] + 1);
        }
        if (j + 1 < n) {
          dp[i][j] = Math.min(dp[i][j], dp[i][j + 1] + 1);
        }
      }
    }
    return dp;
  }
}

统计信息

通过次数	提交次数	AC比率
76442	167102	45.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途