558-四叉树交集(Logical OR of Two Binary Grids Represented as Quad-Trees)
发表于：2021-12-03 | 分类： 中等
字数统计: 1.7k | 阅读时长: 8分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/logical-or-of-two-binary-grids-represented-as-quad-trees

英文原文

A Binary Matrix is a matrix in which all the elements are either 0 or 1.

Given quadTree1 and quadTree2. quadTree1 represents a n * n binary matrix and quadTree2 represents another n * n binary matrix. 

Return a Quad-Tree representing the n * n binary matrix which is the result of logical bitwise OR of the two binary matrixes represented by quadTree1 and quadTree2.

Notice that you can assign the value of a node to True or False when isLeaf is False, and both are accepted in the answer.

A Quad-Tree is a tree data structure in which each internal node has exactly four children. Besides, each node has two attributes:

  • val: True if the node represents a grid of 1's or False if the node represents a grid of 0's. 
  • isLeaf: True if the node is leaf node on the tree or False if the node has the four children.
class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

We can construct a Quad-Tree from a two-dimensional area using the following steps:

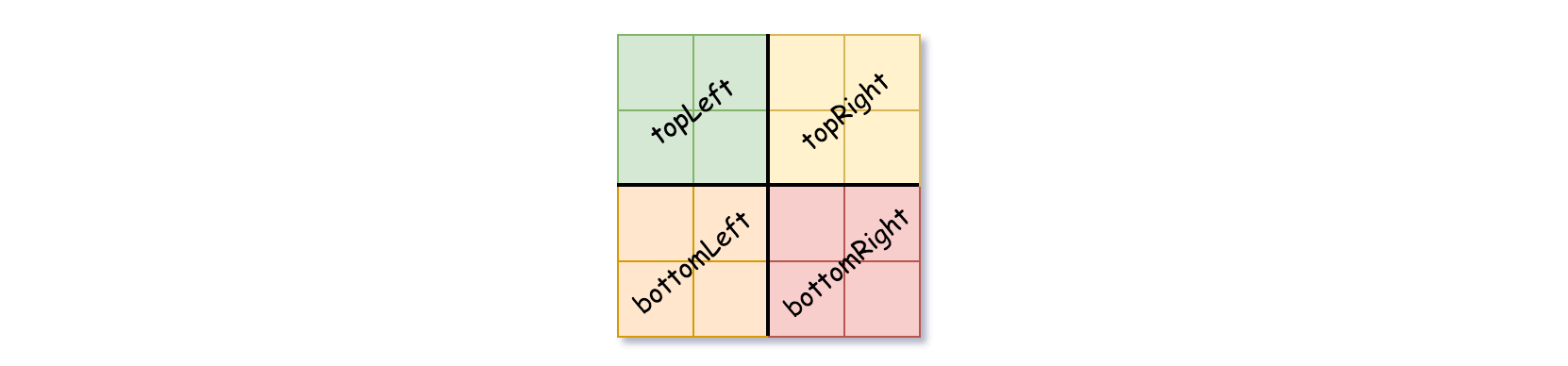
  1. If the current grid has the same value (i.e all 1's or all 0's) set isLeaf True and set val to the value of the grid and set the four children to Null and stop.
  2. If the current grid has different values, set isLeaf to False and set val to any value and divide the current grid into four sub-grids as shown in the photo.
  3. Recurse for each of the children with the proper sub-grid.

If you want to know more about the Quad-Tree, you can refer to the wiki.

Quad-Tree format:

The input/output represents the serialized format of a Quad-Tree using level order traversal, where null signifies a path terminator where no node exists below.

It is very similar to the serialization of the binary tree. The only difference is that the node is represented as a list [isLeaf, val].

If the value of isLeaf or val is True we represent it as 1 in the list [isLeaf, val] and if the value of isLeaf or val is False we represent it as 0.

 

Example 1:

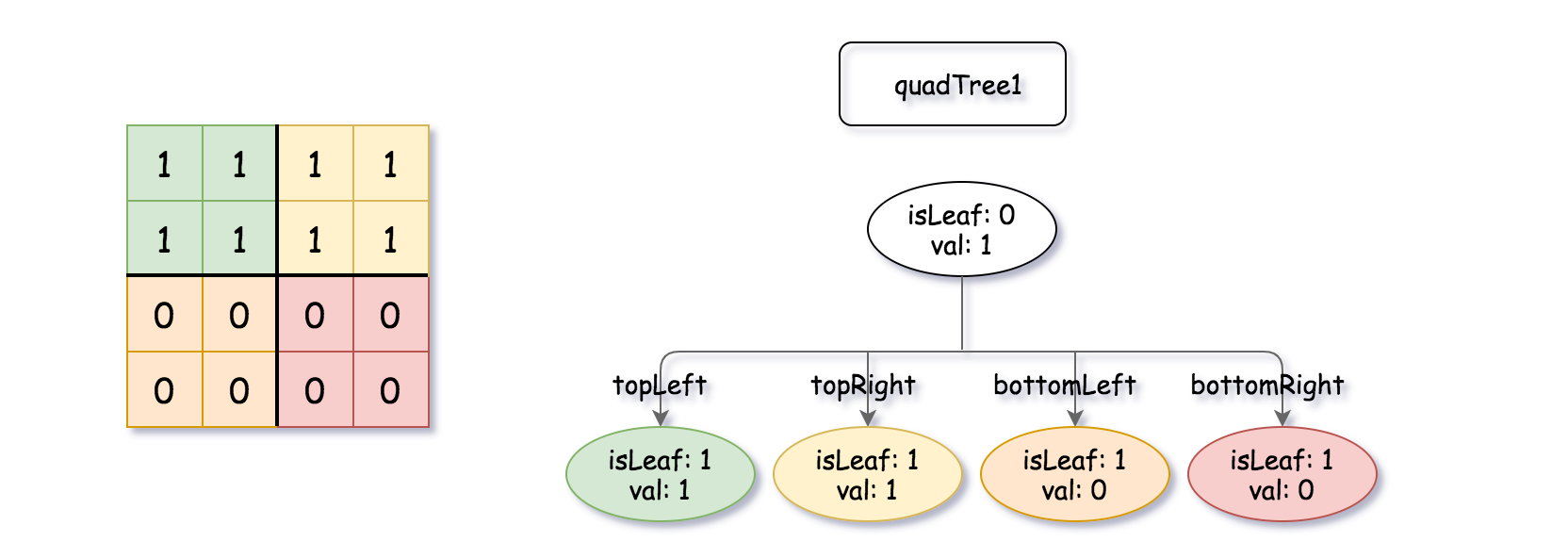
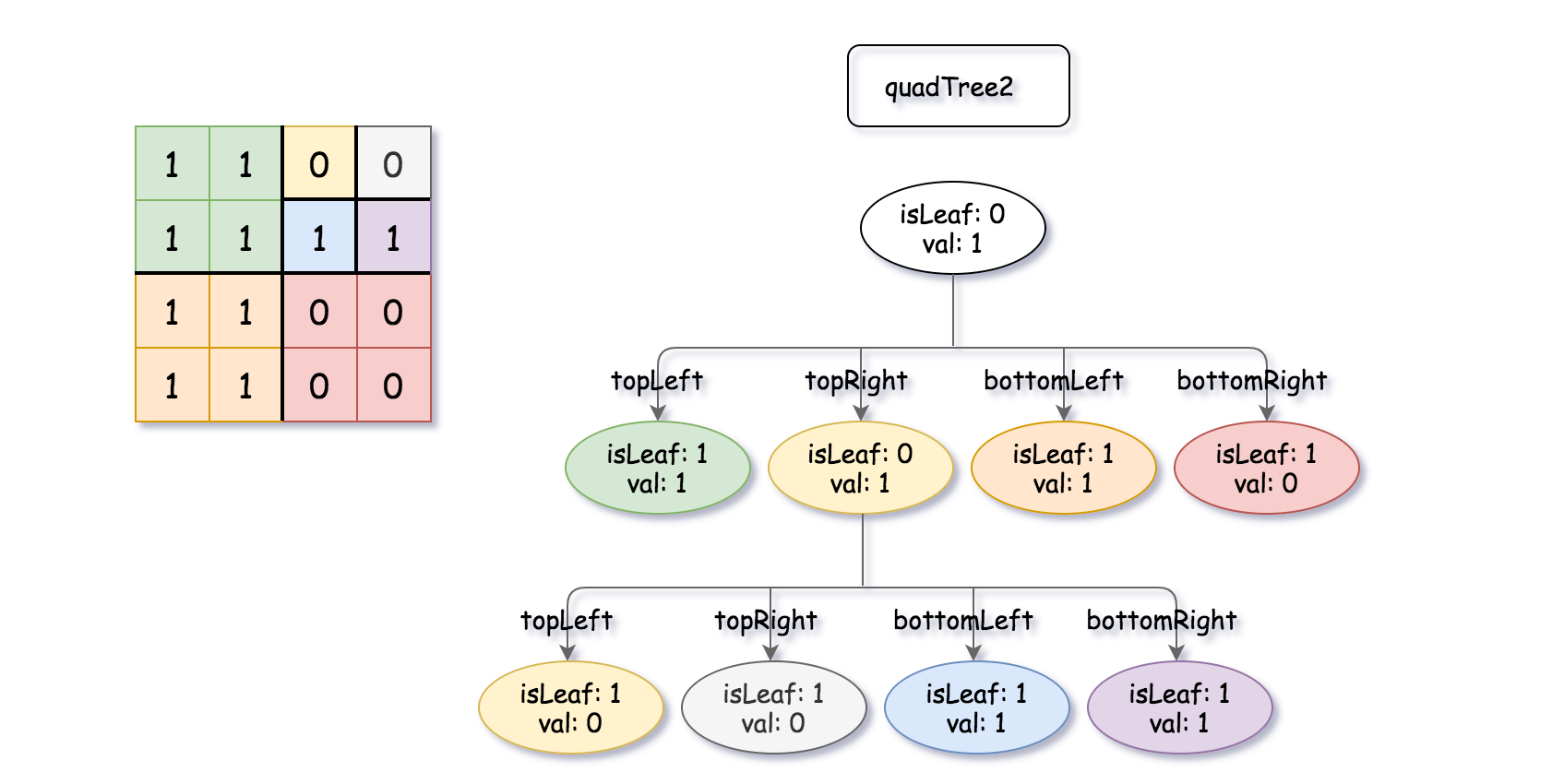
Input: quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
Output: [[0,0],[1,1],[1,1],[1,1],[1,0]]
Explanation: quadTree1 and quadTree2 are shown above. You can see the binary matrix which is represented by each Quad-Tree.
If we apply logical bitwise OR on the two binary matrices we get the binary matrix below which is represented by the result Quad-Tree.
Notice that the binary matrices shown are only for illustration, you don't have to construct the binary matrix to get the result tree.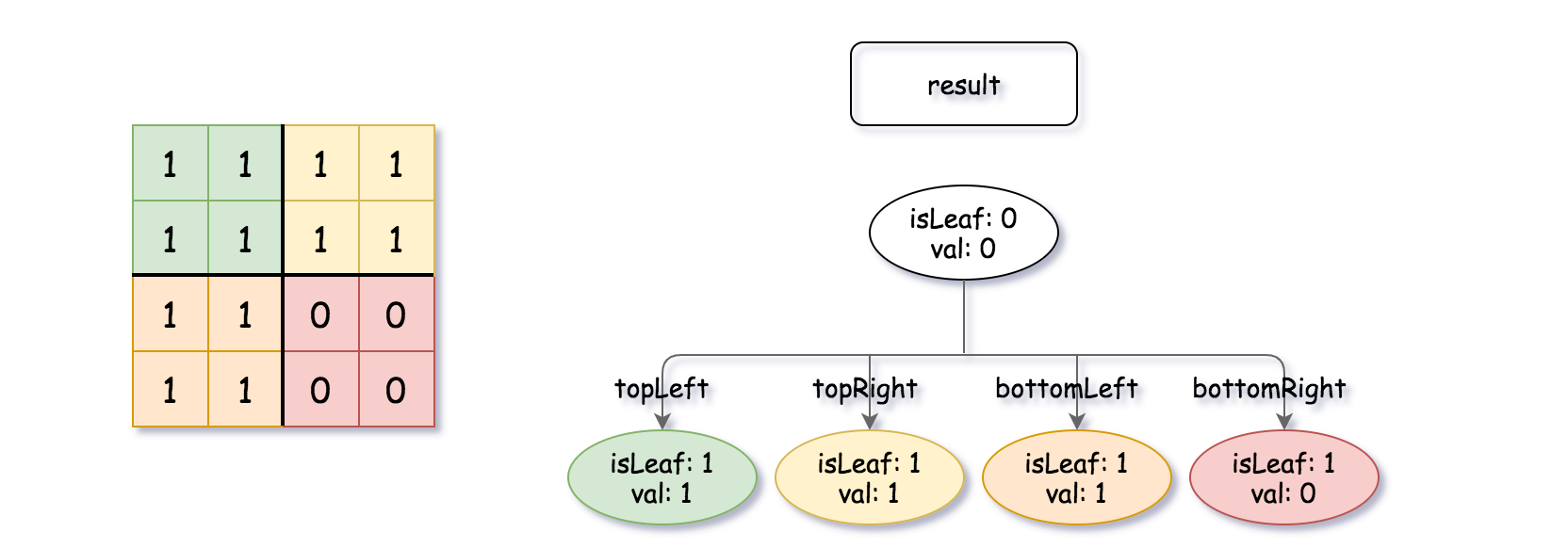

Example 2:

Input: quadTree1 = [[1,0]]
, quadTree2 = [[1,0]]
Output: [[1,0]]
Explanation: Each tree represents a binary matrix of size 1*1. Each matrix contains only zero.
The resulting matrix is of size 1*1 with also zero.

Example 3:

Input: quadTree1 = [[0,0],[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[1,1],[1,0],[1,1]]
Output: [[1,1]]

Example 4:

Input: quadTree1 = [[0,0],[1,1],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]
Output: [[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]

Example 5:

Input: quadTree1 = [[0,1],[1,0],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,1],[0,1],[1,0],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1]]
Output: [[0,0],[0,1],[0,1],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1],[1,0],[1,0],[1,1],[1,1]]

 

Constraints:

  • quadTree1 and quadTree2 are both valid Quad-Trees each representing a n * n grid.
  • n == 2^x where 0 <= x <= 9.

中文题目

二进制矩阵中的所有元素不是 0 就是 1 。

给你两个四叉树，quadTree1 和 quadTree2。其中 quadTree1 表示一个 n * n 二进制矩阵，而 quadTree2 表示另一个 n * n 二进制矩阵。

请你返回一个表示 n * n 二进制矩阵的四叉树，它是 quadTree1 和 quadTree2 所表示的两个二进制矩阵进行 按位逻辑或运算 的结果。

注意，当 isLeaf 为 False 时，你可以把 True 或者 False 赋值给节点，两种值都会被判题机制 接受 。

四叉树数据结构中，每个内部节点只有四个子节点。此外，每个节点都有两个属性：

  • val：储存叶子结点所代表的区域的值。1 对应 True，0 对应 False；
  • isLeaf: 当这个节点是一个叶子结点时为 True，如果它有 4 个子节点则为 False 。
class Node {
    public boolean val;
    public boolean isLeaf;
    public Node topLeft;
    public Node topRight;
    public Node bottomLeft;
    public Node bottomRight;
}

我们可以按以下步骤为二维区域构建四叉树：

  1. 如果当前网格的值相同（即，全为 0 或者全为 1），将 isLeaf 设为 True ，将 val 设为网格相应的值，并将四个子节点都设为 Null 然后停止。
  2. 如果当前网格的值不同，将 isLeaf 设为 False， 将 val 设为任意值，然后如下图所示，将当前网格划分为四个子网格。
  3. 使用适当的子网格递归每个子节点。

如果你想了解更多关于四叉树的内容，可以参考 wiki 。

四叉树格式：

输出为使用层序遍历后四叉树的序列化形式，其中 null 表示路径终止符，其下面不存在节点。

它与二叉树的序列化非常相似。唯一的区别是节点以列表形式表示 [isLeaf, val] 。

如果 isLeaf 或者 val 的值为 True ，则表示它在列表 [isLeaf, val] 中的值为 1 ；如果 isLeaf 或者 val 的值为 False ，则表示值为 0 。

 

示例 1：

输入：quadTree1 = [[0,1],[1,1],[1,1],[1,0],[1,0]]
, quadTree2 = [[0,1],[1,1],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[1,1],[1,1],[1,1],[1,0]]
解释：quadTree1 和 quadTree2 如上所示。由四叉树所表示的二进制矩阵也已经给出。
如果我们对这两个矩阵进行按位逻辑或运算，则可以得到下面的二进制矩阵，由一个作为结果的四叉树表示。
注意，我们展示的二进制矩阵仅仅是为了更好地说明题意，你无需构造二进制矩阵来获得结果四叉树。

示例 2：

输入：quadTree1 = [[1,0]]
, quadTree2 = [[1,0]]
输出：[[1,0]]
解释：两个数所表示的矩阵大小都为 1*1，值全为 0 
结果矩阵大小为 1*1，值全为 0 。

示例 3：

输入：quadTree1 = [[0,0],[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[1,1],[1,0],[1,1]]
输出：[[1,1]]

示例 4：

输入：quadTree1 = [[0,0],[1,1],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]
输出：[[0,0],[1,1],[0,1],[1,1],[1,1],null,null,null,null,[1,1],[1,0],[1,0],[1,1]]

示例 5：

输入：quadTree1 = [[0,1],[1,0],[0,1],[1,1],[1,0],null,null,null,null,[1,0],[1,0],[1,1],[1,1]]
, quadTree2 = [[0,1],[0,1],[1,0],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1]]
输出：[[0,0],[0,1],[0,1],[1,1],[1,0],[1,0],[1,0],[1,1],[1,1],[1,0],[1,0],[1,1],[1,1]]

 

提示：

  • quadTree1 和 quadTree2 都是符合题目要求的四叉树，每个都代表一个 n * n 的矩阵。
  • n == 2^x ，其中 0 <= x <= 9.

通过代码

高赞题解

A || B 的意思是指

  • 如果A为叶子节点，并且A的值等于true, 这时直接返回true, 不用管B
  • 如果A为叶子节点，但是A的值等于false, 这时直接返回B就可以了（*注意 即使B不是一个叶子节点，也要直接返回， 可以参照后面的图片）
  • 如果A不为叶子节点， 原理一样，这时看B， 如果B为叶子节点，并且B的值为true, 则直接返回true, 不用管A
  • 如果A不为叶子节点， B为叶子节点，并且B的值为false, 这时直接返回A
  • 如果A和B都不为叶子节点， 这时分别再讲A, B的四个子节点传入下一次递归计算结果
  • 最后， 如果A和B的四个子节点的值都会true的话， 这时需要进行合并为一个节点。
    QQ图片20191130154023_wps图片.jpg

代码示例

class Solution {
public:
	Node* intersect(Node* quadTree1, Node* quadTree2) {

		if (quadTree1->isLeaf) { // 1.如果A是叶子节点
			if (quadTree1->val) { // 2.如果A的值为true则直接返回A树
				return quadTree1;
			}
			else {  
				return quadTree2; // 3.A为叶子但A的值为false, 则返回B树
			}
		}
		if (quadTree2->isLeaf) {  // 4.如果B是叶子节点
			if (quadTree2->val) {  // 5.如果B的值为true则直接返回B树
				return quadTree2;
			}
			else {
				return quadTree1;  // 6.B为叶子节点，但B的值为false，则返回A树
			}
		}
		// 7.A和B都不为叶子节点的情况下，分别递归获取四个方向的子节点
		Node* topLeft = intersect(quadTree1->topLeft, quadTree2->topLeft);
		Node* topRight = intersect(quadTree1->topRight, quadTree2->topRight);
		Node* bottomLeft = intersect(quadTree1->bottomLeft, quadTree2->bottomLeft);
		Node* bottomRight = intersect(quadTree1->bottomRight, quadTree2->bottomRight);
		
		// 8.如果四个节点同时为叶子节点。并且值为true时,则返回的节点进行合并,合并为一个值为true的叶子节点
		if (topLeft->isLeaf && topRight->isLeaf && bottomLeft->isLeaf && bottomRight->isLeaf &&
			topLeft->val && topRight->val && bottomLeft->val && bottomRight->val) {
			return new Node(true, true, NULL, NULL, NULL, NULL);
		}
		// 9. 通过第7步获取得四个方位的节点，构造出一个新的节点树
		return new Node(false, false, topLeft, topRight, bottomLeft, bottomRight);
	}

};

统计信息

通过次数 提交次数 AC比率
3053 6055 50.4%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
树 分治
上一篇:
427-建立四叉树(Construct Quad Tree)
下一篇:
559-N 叉树的最大深度(Maximum Depth of N-ary Tree)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo