原文链接: https://leetcode-cn.com/problems/out-of-boundary-paths

英文原文

There is an m x n grid with a ball. The ball is initially at the position [startRow, startColumn]. You are allowed to move the ball to one of the four adjacent cells in the grid (possibly out of the grid crossing the grid boundary). You can apply at most maxMove moves to the ball.

Given the five integers m, n, maxMove, startRow, startColumn, return the number of paths to move the ball out of the grid boundary. Since the answer can be very large, return it modulo 109 + 7.

 

Example 1:

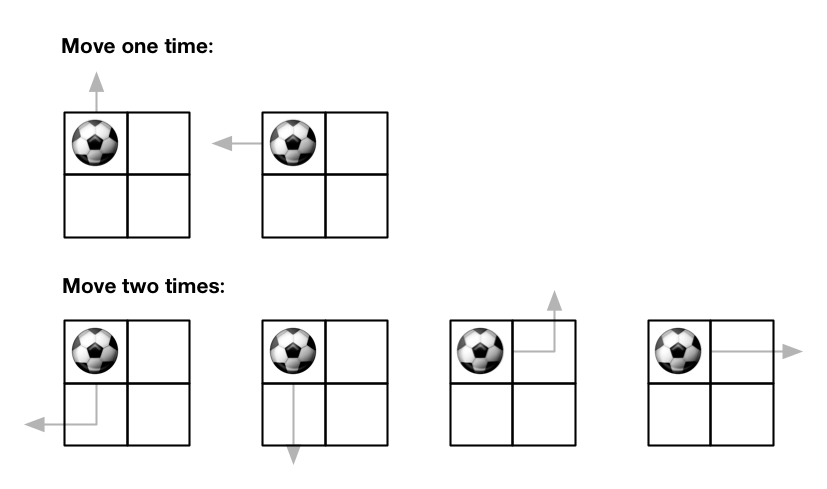
Input: m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
Output: 6

Example 2:

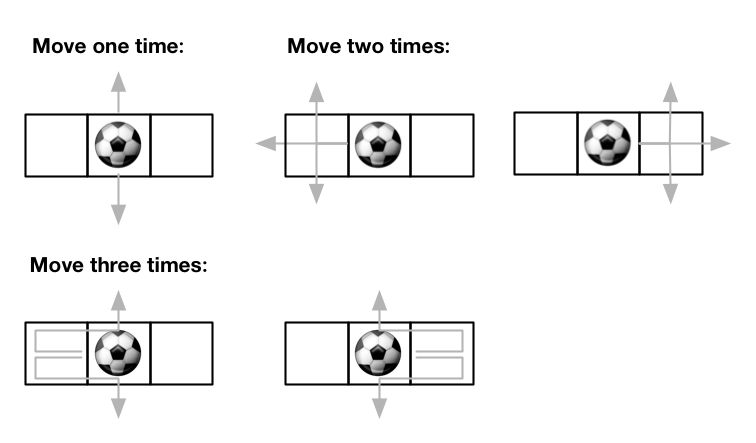
Input: m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
Output: 12

 

Constraints:

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow < m
• 0 <= startColumn < n

中文题目

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你 最多 可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余 后的结果。

 

示例 1：

输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6

示例 2：

输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12

 

提示：

• 1 <= m, n <= 50
• 0 <= maxMove <= 50
• 0 <= startRow < m
• 0 <= startColumn < n

通过代码

高赞题解

解题思路

【先赞后看，养成习惯】
这道题是标准的动态规划题目，属于写出状态转移方程，就可以直接AC的题目。

状态定义

dp[i][j][k]:表示从(i,j)出发第k步出界的路径总数，等价于从外界出发第k步走到(i,j)的路径总数
（可参考题解LeetCode688 “马”在棋盘上的概率）

状态转移

显然我们可以直接获得如下状态转移方程
$$
dp[i][j][k] = dp[i-1][j][k-1]+dp[i+1][j][k-1] + dp[i][j-1][k-1]+dp[i][j+1][k-1]
$$
初始化：我们需要注意外界的坐标的初始状态对应的值为1，即
$$
dp[i][j][0] \xlongequal[]{(i,j) Out of bounds}1
$$
类似的转移方程在其他题目中也有出现哟~
（参考相关题目）

如何求解

有了每一个点的每一步对应的值，我们可以说是什么都不怕了
题目求的是最多移动N次，出界的路径数，因此我们只需要讲每一步对应的值都加起来即可
$$
Sum = \sum_{k=1}^Ndp[i][j][k]
$$

动图展示

<,,,,>

相关题目

LeetCode688 “马”在棋盘上的概率
LeetCode935 骑士拨号器
LeetCode1220 统计元音字母序列的数目

我的题解

LeetCode1262 可被三整除的最大和
LeetCode688 “马”在棋盘上的概率
LeetCode967 连续差相同的数字
LeetCode873 最长的斐波那契子序列的长度
LeetCode1218 最长定差子序列
LeetCode523 连续子数组和

代码

class Solution {
public:
    int findPaths(int m, int n, int N, int i, int j) {
       int MOD = 1000000007;
	if (N == 0) { return 0; }

	vector<vector<vector<unsigned long long int>>> dp(m + 2, vector<vector<unsigned long long int>>(n + 2, vector<unsigned long long int>(N + 1, 0)));
	for (int i = 0; i <= m + 1; i++) {
		dp[i][0][0] = 1;
		dp[i][n + 1][0] = 1;
	}
	for (int i = 0; i <= n + 1; i++) {
		dp[0][i][0] = 1;
		dp[m + 1][i][0] = 1;
	}
	for (int k = 1; k <= N; k++) {
		for (int i = 1; i <= m; i++) {
			for (int j = 1; j <= n; j++) {
				dp[i][j][k] = (dp[i - 1][j][k - 1] + dp[i + 1][j][k - 1] + \
								dp[i][j - 1][k - 1] + dp[i][j + 1][k - 1]) % MOD;
			}
		}
	}
	int sum = 0;
	for (int k = 1; k <= N; k++) {
		sum = (sum + dp[i + 1][j + 1][k]) % MOD;
	}
	return sum;
    }
};

统计信息

通过次数	提交次数	AC比率
26716	57055	46.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
“马”在棋盘上的概率	中等