原文链接: https://leetcode-cn.com/problems/maximum-width-of-binary-tree

英文原文

Given the root of a binary tree, return the maximum width of the given tree.

The maximum width of a tree is the maximum width among all levels.

The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes are also counted into the length calculation.

It is guaranteed that the answer will in the range of 32-bit signed integer.

 

Example 1:

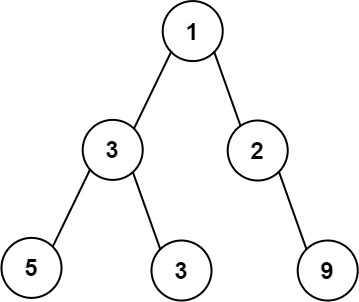
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width existing in the third level with the length 4 (5,3,null,9).

Example 2:

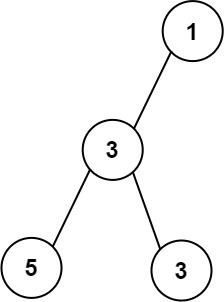
Input: root = [1,3,null,5,3]
Output: 2
Explanation: The maximum width existing in the third level with the length 2 (5,3).

Example 3:

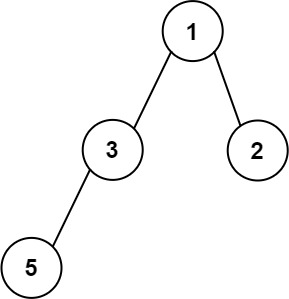
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width existing in the second level with the length 2 (3,2).

Example 4:

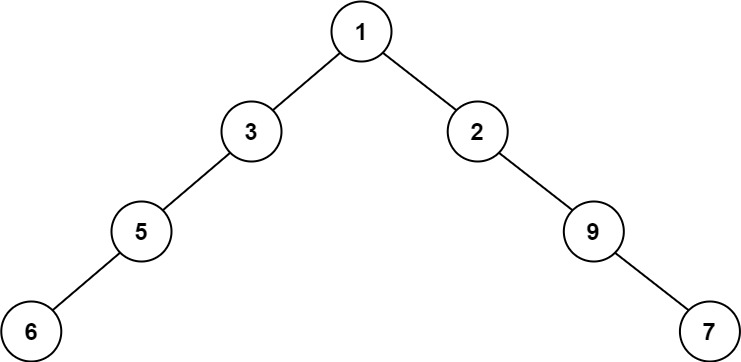
Input: root = [1,3,2,5,null,null,9,6,null,null,7]
Output: 8
Explanation: The maximum width existing in the fourth level with the length 8 (6,null,null,null,null,null,null,7).

 

Constraints:

• The number of nodes in the tree is in the range [1, 3000].
• -100 <= Node.val <= 100

中文题目

给定一个二叉树，编写一个函数来获取这个树的最大宽度。树的宽度是所有层中的最大宽度。这个二叉树与满二叉树（full binary tree）结构相同，但一些节点为空。

每一层的宽度被定义为两个端点（该层最左和最右的非空节点，两端点间的null节点也计入长度）之间的长度。

示例 1:

输入: 

           1
         /   \
        3     2
       / \     \  
      5   3     9 

输出: 4
解释: 最大值出现在树的第 3 层，宽度为 4 (5,3,null,9)。

示例 2:

输入: 

          1
         /  
        3    
       / \       
      5   3     

输出: 2
解释: 最大值出现在树的第 3 层，宽度为 2 (5,3)。

示例 3:

输入: 

          1
         / \
        3   2 
       /        
      5      

输出: 2
解释: 最大值出现在树的第 2 层，宽度为 2 (3,2)。

示例 4:

输入: 

          1
         / \
        3   2
       /     \  
      5       9 
     /         \
    6           7
输出: 8
解释: 最大值出现在树的第 4 层，宽度为 8 (6,null,null,null,null,null,null,7)。

注意: 答案在32位有符号整数的表示范围内。

通过代码

官方题解

方法框架

解释

由于我们需要将给定树中的每个节点都访问一遍，我们需要遍历树。我们可以用深度优先搜索或者宽度优先搜索将树遍历。

这个问题中的主要想法是给每个节点一个 position 值，如果我们走向左子树，那么 position -> position * 2，如果我们走向右子树，那么 position -> positon * 2 + 1。当我们在看同一层深度的位置值 L 和 R 的时候，宽度就是 R - L + 1。

方法 1：宽度优先搜索 [Accepted]

想法和算法

宽度优先搜索顺序遍历每个节点的过程中，我们记录节点的 position 信息，对于每一个深度，第一个遇到的节点是最左边的节点，最后一个到达的节点是最右边的节点。

[]
def widthOfBinaryTree(self, root):
    queue = [(root, 0, 0)]
    cur_depth = left = ans = 0
    for node, depth, pos in queue:
        if node:
            queue.append((node.left, depth+1, pos*2))
            queue.append((node.right, depth+1, pos*2 + 1))
            if cur_depth != depth:
                cur_depth = depth
                left = pos
            ans = max(pos - left + 1, ans)

    return ans

[]
class Solution {
    public int widthOfBinaryTree(TreeNode root) {
        Queue<AnnotatedNode> queue = new LinkedList();
        queue.add(new AnnotatedNode(root, 0, 0));
        int curDepth = 0, left = 0, ans = 0;
        while (!queue.isEmpty()) {
            AnnotatedNode a = queue.poll();
            if (a.node != null) {
                queue.add(new AnnotatedNode(a.node.left, a.depth + 1, a.pos * 2));
                queue.add(new AnnotatedNode(a.node.right, a.depth + 1, a.pos * 2 + 1));
                if (curDepth != a.depth) {
                    curDepth = a.depth;
                    left = a.pos;
                }
                ans = Math.max(ans, a.pos - left + 1);
            }
        }
        return ans;
    }
}

class AnnotatedNode {
    TreeNode node;
    int depth, pos;
    AnnotatedNode(TreeNode n, int d, int p) {
        node = n;
        depth = d;
        pos = p;
    }
}

复杂度分析

• 时间复杂度： $O(N)$，其中 $N$ 是输入树的节点数目，我们遍历每个节点一遍。

• 空间复杂度： $O(N)$，这是 queue 的大小。

方法 2：深度优先搜索 [Accepted]

想法和算法

按照深度优先的顺序，我们记录每个节点的 position 。对于每一个深度，第一个到达的位置会被记录在 left[depth] 中。

然后对于每一个节点，它对应这一层的可能宽度是 pos - left[depth] + 1 。我们将每一层这些可能的宽度去一个最大值就是答案。

[]
class Solution(object):
    def widthOfBinaryTree(self, root):
        self.ans = 0
        left = {}
        def dfs(node, depth = 0, pos = 0):
            if node:
                left.setdefault(depth, pos)
                self.ans = max(self.ans, pos - left[depth] + 1)
                dfs(node.left, depth + 1, pos * 2)
                dfs(node.right, depth + 1, pos * 2 + 1)

        dfs(root)
        return self.ans

[]
class Solution {
    int ans;
    Map<Integer, Integer> left;
    public int widthOfBinaryTree(TreeNode root) {
        ans = 0;
        left = new HashMap();
        dfs(root, 0, 0);
        return ans;
    }
    public void dfs(TreeNode root, int depth, int pos) {
        if (root == null) return;
        left.computeIfAbsent(depth, x-> pos);
        ans = Math.max(ans, pos - left.get(depth) + 1);
        dfs(root.left, depth + 1, 2 * pos);
        dfs(root.right, depth + 1, 2 * pos + 1);
    }
}

复杂度分析

• 时间复杂度： $O(N)$ ，其中 $N$ 是树中节点的数目，我们需要遍历每个节点。

• 空间复杂度： $O(N)$ ，这部分空间是因为我们 DFS 递归过程中有 $N$ 层的栈。

此分析方法由 @awice 提供。

统计信息

通过次数	提交次数	AC比率
31426	76903	40.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言