684-冗余连接(Redundant Connection)
发表于：2021-12-03 | 分类： 中等
字数统计: 411 | 阅读时长: 2分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/redundant-connection

英文原文

In this problem, a tree is an undirected graph that is connected and has no cycles.

You are given a graph that started as a tree with n nodes labeled from 1 to n, with one additional edge added. The added edge has two different vertices chosen from 1 to n, and was not an edge that already existed. The graph is represented as an array edges of length n where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the graph.

Return an edge that can be removed so that the resulting graph is a tree of n nodes. If there are multiple answers, return the answer that occurs last in the input.

 

Example 1:

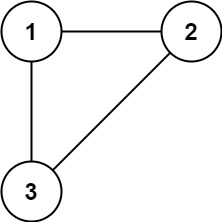
Input: edges = [[1,2],[1,3],[2,3]]
Output: [2,3]

Example 2:

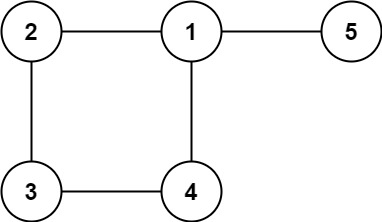
Input: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
Output: [1,4]

 

Constraints:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • There are no repeated edges.
  • The given graph is connected.

中文题目

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

 

示例 1：

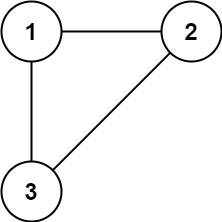
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

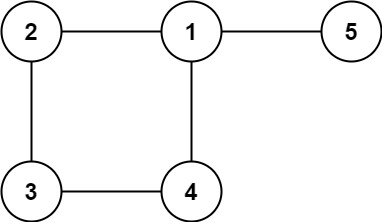
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

 

提示:

  • n == edges.length
  • 3 <= n <= 1000
  • edges[i].length == 2
  • 1 <= ai < bi <= edges.length
  • ai != bi
  • edges 中无重复元素
  • 给定的图是连通的 

通过代码

高赞题解

官方题解把并查集的原理和用法讲得很明白了

但是在具体实现上没有说。

我这里简单说一下吧，希望能帮助对并查集不熟的小伙伴快速上手

具体落实到这个题上，通俗讲解一下

先明确几个概念

1.集合树：所有节点以代表节点为父节点构成的多叉树

2.节点的代表节点：可以理解为节点的父节点，从当前节点出发，可以向上找到的第一个节点

3.集合的代表节点：可以理解为根节点，意味着该集合内所有节点向上走，最终都能到达的节点

来个图帮助理解

image.png

上图中是一棵集合树，树中有1-6总计6个节点

整个集合的代表节点是1

4节点的代表节点是3，6节点的代表节点是1

无论沿着哪个节点向上走，最终都会达到集合代表节点的1节点

然后具体到这个题上：

我们以这个边集合为例子[[1,2], [3,4], [3,2], [1,4], [1,5]]

一、首先，对于边集合edges的每个元素，我们将其看作两个节点集合

比如边[2, 3],我们将其看作节点集合2，和节点集合3

二、在没有添加边的时候，各个节点集合独立，我们需要初始化各个节点集合的代表节点为其自身

所以，我们先初始化一个容器vector，使得vector[i]=i

这里两个i意思不同，作为索引的i是指当前节点，作为值的i是指当前节点所在集合的代表节点

比如vector[2] = 2，意味着2这个节点所在集合的代表节点就是2，没有添加边的情况下，所有节点单独成集合，自身就是代表节点

初始化后，集合图如下图所示：

image.png

三、然后我们开始遍历边集合，将边转化为集合的关系

这里有一点很重要：边[a,b]意味着a所在集合可以和b所在集合合并。

合并方法很多，这里我们简单地将a集合的代表节点戳到b集合的代表节点上

这意味着，将b集合代表节点作为合并后大集合的代表节点

对于一个集合的代表节点s，一定有s->s，意思是s如果是代表节点，那么它本身不存在代表节点

假设我们的读取顺序为[[1,2], [3,4], [3,2], [1,4], [1,5]]

初始化vector[0, 1, 2, 3, 4, 5]

对应的index [0, 1, 2, 3, 4, 5]

##########################################################################

1.读取[1,2]：

读取顺序为[[1,2], [3,4], [3,2], [1,4], [1,5]]

当前vector[0, 1, 2, 3, 4, 5]

当前index [0, 1, 2, 3, 4, 5]

原本1->1，2->2，

由1节点出发，vector[1]=1, 找到1所在集合的代表节点1

由2节点出发，vector[2]=2, 找到2所在集合的代表节点2

于是，将1的代表置为2，vector[1]=2, vector[2]=2

对应的vector[0, 2, 2, 3, 4, 5]

对应的index [0, 1, 2, 3, 4, 5]

原集合变为下图：

image.png

##########################################################################

2.读取[3, 4]

读取顺序为[[1,2], [3,4], [3,2], [1,4], [1,5]]

当前vector[0, 2, 2, 3, 4, 5]

当前index [0, 1, 2, 3, 4, 5]

同理，将3所在集合的的代表节点3的代表节点置为4

对应的vector[0, 2, 2, 4, 4, 5]

对应的index [0, 1, 2, 3, 4, 5]

集合变化如下图：

image.png

##########################################################################

3.读取[3, 2]

读取顺序为[[1,2], [3,4], [3,2], [1,4], [1,5]]

当前vector[0, 2, 2, 4, 4, 5]

当前index [0, 1, 2, 3, 4, 5]

从节点3出发，vector[3]=4, vector[4]=4,于是找到节点3所在集合的代表节点为4

从节点2出发，vector[2]=2, 找到节点2所在集合的代表节点为2

于是，将4的代表置为2，vector[4]=2, vector[2]=2

对应的vector[0, 2, 2, 4, 2, 5]

对应的index [0, 1, 2, 3, 4, 5]

集合变化如下图：

image.png

##########################################################################

4.读取[1, 4]

读取顺序为[[1,2], [3,4], [3,2], [1,4], [1,5]]

当前vector[0, 2, 2, 4, 2, 5]

当前index [0, 1, 2, 3, 4, 5]

从节点1出发，vector[1]=2, vector[2]=2, 找到节点1所在集合代表节点为2

从节点4出发，vector[4]=2, vector[2]=2, 找到节点4所在集合代表节点为2

由于1和4的代表节点相同，说明这两个节点本身就在同一个集合中

由于原图是无向图，路径是双向可达的，1能够到达2,而且2能够到达4，再加上1能够到达4

说明1能通过两条路径到达4，,这也意味着这条边出现的时候，原图中一定出现了环

至于题中要求的，返回最后一条边，其实这就是返回添加过后会构成环的那一条边

直白解释就是，在这条边出现之前，图中没有环

这条边出现，图中也出现环。包括这条边在内，构成环的边都是满足破圈条件的边

然而谁是最后一条出现在边集合里的？当然，就是这条构成环的最后一条边

##########################################################################

到这里，对于此题的实现基本上说完了，直接上代码吧


class Solution {

public:

    vector<int> findRedundantConnection(vector<vector<int>>& edges) {

        vector<int> rp(1001);

        int sz = edges.size();

        // 初始化各元素为单独的集合，代表节点就是其本身

        for(int i=0;i<sz;i++)

            rp[i] = i;

        for(int j=0;j<sz;j++){

            // 找到边上两个节点所在集合的代表节点

            int set1 = find(edges[j][0], rp);

            int set2 = find(edges[j][1], rp);

            if(set1 == set2)  // 两个集合代表节点相同，说明出现环，返回答案

                return edges[j]; 

            else    // 两个集合独立，合并集合。将前一个集合代表节点戳到后一个集合代表节点上

                rp[set1] = set2;

        }

        return {0, 0};

    }



    // 查找路径并返回代表节点，实际上就是给定当前节点，返回该节点所在集合的代表节点

    // 之前这里写的压缩路径，引起歧义，因为结果没更新到vector里，所以这里改成路径查找比较合适

    // 感谢各位老哥的提议

    int find(int n, vector<int> &rp){

        int num = n;

        while(rp[num] != num)

            num = rp[num];

        return num;

    }

};

#####################################################################

证明部分

下面是响应某大佬建议，增加的一部分证明，有需要的同学就看看吧

证明一下为什么给定一条新的边，两头节点在同一个集合，就意味着出现了环

这里有个大前提，因为是无向图，集合里不会同时出现[1,2]和[2,1]这种重合边

上面的代码遇到集合里有重合边的情况是会出现误判的

就拿这个[1,2]和[2,1]来举例

给定[1,2]后，再读取[2,1]，两个节点在同一个集合，然而并没有出现环。

所以，这里代码工作的前提是不出现重合边

#####################################################################

下面回到最初的问题，为什么给定新边的两个节点在同一集合就意味着出现了环

假设给定新边的两个节点分别为5,6，新边为[5,6]

####对于一条新出现的边，总共有两种情况，两个节点之一单独成集合，两个节点均不单独成集合

第一种情况，两个节点之一单独成集合

假设5单独成集合。这种情况下，两个节点不可能在一个集合里

因为有一个独立集合（只有节点5），6所在的集合和这个集合必然没有交集

之后这两个集合进行合并操作

直观点理解就是，5单独成集合，意味着5第一次出现在图里

这里只有新边和5相关，所以当前只给定一条和5相关的边，对5而言，就像只举起了一只手

要形成环，环上每个节点都必须是举起两只手的

所以这种情况下是不可能出现环的，程序中也是这样判定的

第二种情况，两个节点均不单独成集合

这里也可以细分为5和6是否作为该集合的代表节点

假设5所在集合代表节点为a

6所在集合代表节点也为a

2.1第一个分支，如果a不为5和6本身，那么就有5->…->a，6->…->a，路径双向可达
可以得到5->...->a->...->6,对于给定边[5,6]可得5->6

所以5到达6有两条路径，出现了环。
2.2第二个分支，a为5和6之一
假设，a为5
2.2.1 首先考虑，6直接指向5这种情况
出现这种情况，只能是在已经存在集合x->...->6时，出现[...,5]这样的边

其中，...为x->...->6路径上除6以外任意节点

此时...的代表节点为6，5的代表节点为5，合并，6戳到5上，于是出现了6直接指向5

这种情况下，已经存在6->...->5一条路径，再读取到[5,6]，环出现了
2.2.2 再考虑6不直接指向5的情况，就简单很多了，6->x->5
再读取到[5,6]，6可以通过两条路径到达5，出现环

综上，在边集合没有重合边的情况下，如果给定新边的两个节点在同一集合中，说明图中出现了环

统计信息

通过次数 提交次数 AC比率
63153 94743 66.7%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言

相似题目

题目 难度
冗余连接 II 困难
账户合并 中等
深度优先搜索 广度优先搜索 图 并查集
上一篇:
680-验证回文字符串 Ⅱ(Valid Palindrome II)
下一篇:
685-冗余连接 II(Redundant Connection II)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo