原文链接: https://leetcode-cn.com/problems/employee-importance

英文原文

You have a data structure of employee information, including the employee's unique ID, importance value, and direct subordinates' IDs.

You are given an array of employees employees where:

• employees[i].id is the ID of the ith employee.
• employees[i].importance is the importance value of the ith employee.
• employees[i].subordinates is a list of the IDs of the direct subordinates of the ith employee.

Given an integer id that represents an employee's ID, return the total importance value of this employee and all their direct and indirect subordinates.

 

Example 1:

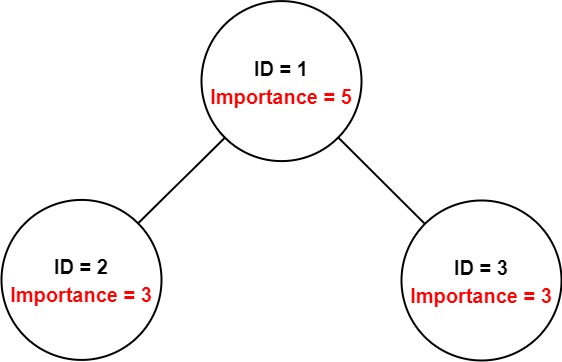
Input: employees = [[1,5,[2,3]],[2,3,[]],[3,3,[]]], id = 1
Output: 11
Explanation: Employee 1 has an importance value of 5 and has two direct subordinates: employee 2 and employee 3.
They both have an importance value of 3.
Thus, the total importance value of employee 1 is 5 + 3 + 3 = 11.

Example 2:

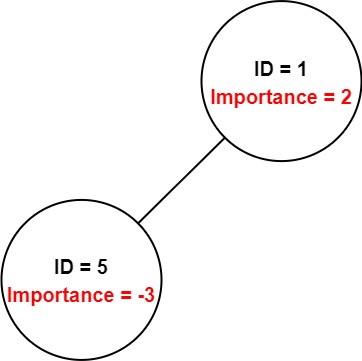
Input: employees = [[1,2,[5]],[5,-3,[]]], id = 5
Output: -3
Explanation: Employee 5 has an importance value of -3 and has no direct subordinates.
Thus, the total importance value of employee 5 is -3.

 

Constraints:

• 1 <= employees.length <= 2000
• 1 <= employees[i].id <= 2000
• All employees[i].id are unique.
• -100 <= employees[i].importance <= 100
• One employee has at most one direct leader and may have several subordinates.
• The IDs in employees[i].subordinates are valid IDs.

中文题目

给定一个保存员工信息的数据结构，它包含了员工 唯一的 id ，重要度 和 直系下属的 id 。

比如，员工 1 是员工 2 的领导，员工 2 是员工 3 的领导。他们相应的重要度为 15 , 10 , 5 。那么员工 1 的数据结构是 [1, 15, [2]] ，员工 2的 数据结构是 [2, 10, [3]] ，员工 3 的数据结构是 [3, 5, []] 。注意虽然员工 3 也是员工 1 的一个下属，但是由于 并不是直系 下属，因此没有体现在员工 1 的数据结构中。

现在输入一个公司的所有员工信息，以及单个员工 id ，返回这个员工和他所有下属的重要度之和。

 

示例：

输入：[[1, 5, [2, 3]], [2, 3, []], [3, 3, []]], 1
输出：11
解释：
员工 1 自身的重要度是 5 ，他有两个直系下属 2 和 3 ，而且 2 和 3 的重要度均为 3 。因此员工 1 的总重要度是 5 + 3 + 3 = 11 。

 

提示：

• 一个员工最多有一个 直系 领导，但是可以有多个 直系 下属
• 员工数量不超过 2000 。

通过代码

高赞题解

递归 / DFS

一个直观的做法是，写一个递归函数来统计某个员工的总和。

统计自身的 $importance$ 值和直系下属的 $importance$ 值。同时如果某个下属还有下属的话，则递归这个过程。

代码（感谢 @answerer 和 @Benhao 同学提供的其他语言版本）：

[]
class Solution {
    Map<Integer, Employee> map = new HashMap<>();
    public int getImportance(List<Employee> es, int id) {
        int n = es.size();
        for (int i = 0; i < n; i++) map.put(es.get(i).id, es.get(i));
        return getVal(id);
    }
    int getVal(int id) {
        Employee master = map.get(id);
        int ans = master.importance;
        for (int oid : master.subordinates) {
            Employee other = map.get(oid);
            ans += other.importance;
            for (int sub : other.subordinates) ans += getVal(sub);
        }
        return ans;
    }
}

[]
class Solution {
public:
    map<int, Employee *> m;
    int getImportance(vector <Employee*> es, int id) {
        int n = es.size();
        for (int i = 0; i < n; i++) 
            m.insert({es[i]->id, es[i]});
        return getVal(id);
    }
    int getVal(int id) {
        Employee * master = m[id];
        int ans = master->importance;
        for (int & oid : master->subordinates) {
            Employee * other = m[oid];
            ans += other->importance;
            for (int & sub : other->subordinates) ans += getVal(sub);
        }
        return ans;
    }
};

[]
class Solution:
    def getImportance(self, employees: List['Employee'], id: int) -> int:
        employees_dict = {employee.id: employee for employee in employees}

        def dfs(employee_id):
            employee = employees_dict[employee_id]
            return employee.importance + sum(dfs(emp_id) for emp_id in employee.subordinates)

        return dfs(id)

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

---

迭代 / BFS

另外一个做法是使用「队列」来存储所有将要计算的 $Employee$ 对象，每次弹出时进行统计，并将其「下属」添加到队列尾部。

代码（感谢 @answerer 同学提供的其他语言版本）：

[]
class Solution {
    public int getImportance(List<Employee> es, int id) {
        int n = es.size();
        Map<Integer, Employee> map = new HashMap<>();
        for (int i = 0; i < n; i++) map.put(es.get(i).id, es.get(i));
        int ans = 0;
        Deque<Employee> d = new ArrayDeque<>();
        d.addLast(map.get(id));
        while (!d.isEmpty()) {
            Employee poll = d.pollFirst();
            ans += poll.importance;
            for (int oid : poll.subordinates) {
                d.addLast(map.get(oid));
            }
        }
        return ans;
    }
}

[]
class Solution {
public:
    map<int, Employee *> m;
    int getImportance(vector <Employee*> es, int id) {
        int n = es.size();
        for (int i = 0; i < n; i++) m.insert({es[i]->id, es[i]});
        int ans = 0;
        deque<Employee *> d;
        d.emplace_back(m[id]);
        while (!d.empty()) {
            Employee * poll = d.front();
            d.pop_front();
            ans += poll->importance;
            for (int & oid : poll->subordinates) {
                d.emplace_back(m[oid]);
            }
        }
        return ans;
    }
};

• 时间复杂度：$O(n)$
• 空间复杂度：$O(n)$

统计信息

通过次数	提交次数	AC比率
57296	88355	64.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
嵌套列表权重和	中等