原文链接: https://leetcode-cn.com/problems/insert-into-a-binary-search-tree

英文原文

You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.

Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.

 

Example 1:

Input: root = [4,2,7,1,3], val = 5
Output: [4,2,7,1,3,5]
Explanation: Another accepted tree is: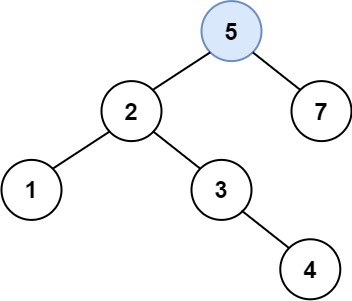

Example 2:

Input: root = [40,20,60,10,30,50,70], val = 25
Output: [40,20,60,10,30,50,70,null,null,25]

Example 3:

Input: root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
Output: [4,2,7,1,3,5]

 

Constraints:

• The number of nodes in the tree will be in the range [0, 104].
• -108 <= Node.val <= 108
• All the values Node.val are unique.
• -108 <= val <= 108
• It's guaranteed that val does not exist in the original BST.

中文题目

给定二叉搜索树（BST）的根节点和要插入树中的值，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

注意，可能存在多种有效的插入方式，只要树在插入后仍保持为二叉搜索树即可。 你可以返回 任意有效的结果 。

 

示例 1：

输入：root = [4,2,7,1,3], val = 5
输出：[4,2,7,1,3,5]
解释：另一个满足题目要求可以通过的树是：

示例 2：

输入：root = [40,20,60,10,30,50,70], val = 25
输出：[40,20,60,10,30,50,70,null,null,25]

示例 3：

输入：root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
输出：[4,2,7,1,3,5]

 

 

提示：

• 给定的树上的节点数介于 0 和 10^4 之间
• 每个节点都有一个唯一整数值，取值范围从 0 到 10^8
• -10^8 <= val <= 10^8
• 新值和原始二叉搜索树中的任意节点值都不同

通过代码

高赞题解

想必刷题刷到这里，你已经知道了二叉搜索树的定义和性质了。不了解的话我在这里再说明一下：

二叉搜索树： 对于树上的每个节点来说，该节点的左子树里所有的节点都小于当前节点，该节点的右子树里所有的节点都大于当前节点。

本题是在「二叉搜索树中插入目标值」，这是一道非常常见的题目，在大学数据结构课程中，老师直接就会在课堂中讲解。同样的题目有 「二叉搜索树中查找目标值」，详见 700. 二叉搜索树中的搜索。两者解法大同小异，有迭代和递归两种写法。

---

迭代解法

• 如果 root 是空，则新建树节点作为根节点返回即可。
• 否则：
  1. 初始化 cur 指向 root。
  2. 比较 cur.val 与目标值的大小关系：
     • 如果 cur.val 大于目标值，说明目标值应当插入 cur 的左子树中，如果 cur.left 为 null，表明这是目标值可以插入的位置，直接插入并返回即可；否则 cur 指向 cur.left，重复步骤 2；
     • 如果 cur.val 小于目标值，说明目标值应当插入 cur 的右子树中。如果 cur.right 为 null，表明这是目标值可以插入的位置，直接插入并返回即可；否则 cur 指向 cur.right，重复步骤 2。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        TreeNode node = new TreeNode(val);
        if (root == null) {
            return node;
        }

        TreeNode cur = root;
        while (true) {
            if (cur.val > val) {
                if (cur.left == null) {
                    cur.left = node;
                    break;
                }
                cur = cur.left;
            } else {
                if (cur.right == null) {
                    cur.right = node;
                    break;
                } 
                cur = cur.right;
            }
        }
        return root;
    }
}

递归解法

递归的写法还是简洁明了的，过程如下：

• 如果 root 是空，则新建树节点作为根节点返回即可。
• 否则比较 root.val 与目标值的大小关系：
  • 如果 root.val 大于目标值，说明目标值应当插入 root 的左子树中，问题变为了在 root.left 中插入目标值，递归调用当前函数；
  • 如果 root.val 小于目标值，说明目标值应当插入 root 的右子树中，问题变为了在 root.right 中插入目标值，递归调用当前函数。

class Solution {
    public TreeNode insertIntoBST(TreeNode root, int val) {
        if (root == null) {
            return new TreeNode(val);
        }

        if (root.val < val) {
            root.right = insertIntoBST(root.right, val);
        } else {
            root.left = insertIntoBST(root.left, val);
        }
        return root;
    }
}

复杂度分析

二叉搜索树的平均深度是 $\log n$，最坏情况是由于有序插入数据导致二叉搜索树退化成一条链表，此时深度是 $n$。因此上述两种解法的平均时间复杂度是 $O(\log n)$，最坏时间复杂度是 $O(n)$。迭代写法的空间复杂度是 $O(1)$，递归写法由于递归调用时会使用方法栈，而方法栈的深度就是二叉搜索树的深度，所以最坏空间复杂度是 $O(n)$。

所以说，二叉搜索树的深度是非常影响查找/插入性能的，所以说并不常用，广泛使用的是平衡搜索树。常见的平衡搜索树有 红黑树，B- 树，B+ 树（还有 ACM/OI 大佬们爱的 treap，splay，SBT）等。比如 Java 里的 TreeMap，TreeSet 和 HashMap 中链表的树化都是用红黑树实现的，又比如 InnoDB 的索引存储就是 B+ 树实现的。感兴趣的同学可以去学习下～学成归来之时，可以问候别人——能不能心里有点 B 树～

☎️ 关注我

统计信息

通过次数	提交次数	AC比率
84612	117251	72.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
二叉搜索树中的搜索	简单