764-最大加号标志(Largest Plus Sign)
发表于：2021-12-03 | 分类： 中等
字数统计: 1.7k | 阅读时长: 8分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/largest-plus-sign

英文原文

You are given an integer n. You have an n x n binary grid grid with all values initially 1's except for some indices given in the array mines. The ith element of the array mines is defined as mines[i] = [xi, yi] where grid[xi][yi] == 0.

Return the order of the largest axis-aligned plus sign of 1's contained in grid. If there is none, return 0.

An axis-aligned plus sign of 1's of order k has some center grid[r][c] == 1 along with four arms of length k - 1 going up, down, left, and right, and made of 1's. Note that there could be 0's or 1's beyond the arms of the plus sign, only the relevant area of the plus sign is checked for 1's.

 

Example 1:

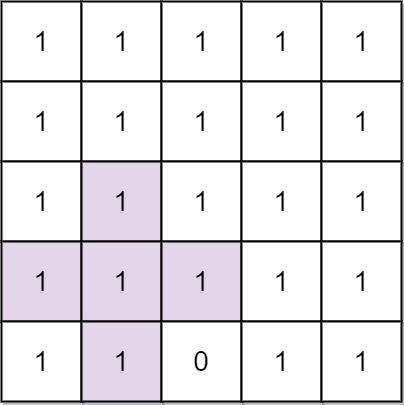
Input: n = 5, mines = [[4,2]]
Output: 2
Explanation: In the above grid, the largest plus sign can only be of order 2. One of them is shown.

Example 2:

Input: n = 1, mines = [[0,0]]
Output: 0
Explanation: There is no plus sign, so return 0.

 

Constraints:

  • 1 <= n <= 500
  • 1 <= mines.length <= 5000
  • 0 <= xi, yi < n
  • All the pairs (xi, yi) are unique.

中文题目

在一个大小在 (0, 0) 到 (N-1, N-1) 的2D网格 grid 中，除了在 mines 中给出的单元为 0，其他每个单元都是 1。网格中包含 1 的最大的轴对齐加号标志是多少阶？返回加号标志的阶数。如果未找到加号标志，则返回 0。

一个 k" 阶由 1 组成的“轴对称”加号标志具有中心网格  grid[x][y] = 1 ，以及4个从中心向上、向下、向左、向右延伸，长度为 k-1，由 1 组成的臂。下面给出 k" 阶“轴对称”加号标志的示例。注意，只有加号标志的所有网格要求为 1，别的网格可能为 0 也可能为 1。

 

k 阶轴对称加号标志示例:

阶 1:
000
010
000

阶 2:
00000
00100
01110
00100
00000

阶 3:
0000000
0001000
0001000
0111110
0001000
0001000
0000000

 

示例 1：

输入: N = 5, mines = [[4, 2]]
输出: 2
解释:

11111
11111
11111
11111
11011

在上面的网格中，最大加号标志的阶只能是2。一个标志已在图中标出。

 

示例 2：

输入: N = 2, mines = []
输出: 1
解释:

11
11

没有 2 阶加号标志，有 1 阶加号标志。

 

示例 3：

输入: N = 1, mines = [[0, 0]]
输出: 0
解释:

0

没有加号标志，返回 0 。

 

提示：

  1. 整数N 的范围： [1, 500].
  2. mines 的最大长度为 5000.
  3. mines[i] 是长度为2的由2个 [0, N-1] 中的数组成.
  4. (另外,使用 C, C++, 或者 C# 编程将以稍小的时间限制进行​​判断.)

 

通过代码

官方题解

方法一： 暴力 【超时】

思路和算法

遍历所有可能的加号中心，找到其中最大的加号。这个算法的时间复杂度为 $O(N^3)$，大致估算的运算量为 $500^3 = (1.25) * 10^8$，这个复杂度是略微高出了题目要求的复杂度的。

[solution1-Python]
class Solution(object):
    def orderOfLargestPlusSign(self, N, mines):
        banned = {tuple(mine) for mine in mines}
        ans = 0
        for r in xrange(N):
            for c in xrange(N):
                k = 0
                while (k <= r < N-k and k <= c < N-k and
                        (r-k, c) not in banned and
                        (r+k, c) not in banned and
                        (r, c-k) not in banned and
                        (r, c+k) not in banned):
                    k += 1
                ans = max(ans, k)
        return ans
[solution2-Java]
class Solution {
    public int orderOfLargestPlusSign(int N, int[][] mines) {
        Set<Integer> banned = new HashSet();
        for (int[] mine: mines)
            banned.add(mine[0] * N + mine[1]);
            
        int ans = 0;
        for (int r = 0; r < N; ++r) for (int c = 0; c < N; ++c) {
            int k = 0;
            while (k <= r && r < N-k && k <= c && c < N-k &&
                    !banned.contains((r-k)*N + c) &&
                    !banned.contains((r+k)*N + c) &&
                    !banned.contains(r*N + c-k) &&
                    !banned.contains(r*N + c+k))
                k++;
            
            ans = Math.max(ans, k);
        }
        return ans;
    }
}

复杂度分析

  • 时间复杂度: $O(N^3)$，遍历整个网格需要 $O(N^2)$，对于每个中心点需要遍历 $O(N)$ 次来找到 k。

  • 空间复杂度: $O(mines.length)$。

方法二： 动态规划 【通过】

思路

怎么提升暴力算法的性能呢？有一个方法就是加快找到 k 的速度。如果我们能预先计算出每个中心的最长臂长 $L_u, L_l, L_d, L_r$，那么就能知道以这个为中心的加号的阶就是 $\min(L_u, L_l, L_d, L_r)$。动态规划可以用来预先计算臂长。

算法

对于每个中心点坐标 (r, c)，从四个方向计算从 (r, c) 开始最长连续 1 的个数。用动态规划的方法来看，如果 grid[r][c] 是 0，那么臂长就是 0，如果 grid[r][c] 是 l, 那么臂长就是当前方向上连续 1 的个数再加 1。
举个例子，假设当前方向为左，网格中有一行为 01110110， 那么对应的连续 1 的个数就是 012301201。可以观察到，每个数要么是它相邻左边的数加 1， 要么是 0。
对于每个中心点，让 dp[r][c] 为四个方向中最小的连续 1 的个数。显然，dp 数组中最大的值就是我们要的结果。

[solution2-Python]
class Solution(object):
    def orderOfLargestPlusSign(self, N, mines):
        banned = {tuple(mine) for mine in mines}
        dp = [[0] * N for _ in xrange(N)]
        ans = 0
        
        for r in xrange(N):
            count = 0
            for c in xrange(N):
                count = 0 if (r,c) in banned else count+1
                dp[r][c] = count
            
            count = 0
            for c in xrange(N-1, -1, -1):
                count = 0 if (r,c) in banned else count+1
                if count < dp[r][c]: dp[r][c] = count
        
        for c in xrange(N):
            count = 0
            for r in xrange(N):
                count = 0 if (r,c) in banned else count+1
                if count < dp[r][c]: dp[r][c] = count
            
            count = 0
            for r in xrange(N-1, -1, -1):
                count = 0 if (r, c) in banned else count+1
                if count < dp[r][c]: dp[r][c] = count
                if dp[r][c] > ans: ans = dp[r][c]
        
        return ans
[solution2-Java]
class Solution {
    public int orderOfLargestPlusSign(int N, int[][] mines) {
        Set<Integer> banned = new HashSet();
        int[][] dp = new int[N][N];
        
        for (int[] mine: mines)
            banned.add(mine[0] * N + mine[1]);
        int ans = 0, count;
        
        for (int r = 0; r < N; ++r) {
            count = 0;
            for (int c = 0; c < N; ++c) {
                count = banned.contains(r*N + c) ? 0 : count + 1;
                dp[r][c] = count;
            }
            
            count = 0;
            for (int c = N-1; c >= 0; --c) {
                count = banned.contains(r*N + c) ? 0 : count + 1;
                dp[r][c] = Math.min(dp[r][c], count);
            }
        }
        
        for (int c = 0; c < N; ++c) {
            count = 0;
            for (int r = 0; r < N; ++r) {
                count = banned.contains(r*N + c) ? 0 : count + 1;
                dp[r][c] = Math.min(dp[r][c], count);
            }
            
            count = 0;
            for (int r = N-1; r >= 0; --r) {
                count = banned.contains(r*N + c) ? 0 : count + 1;
                dp[r][c] = Math.min(dp[r][c], count);
                ans = Math.max(ans, dp[r][c]);
            }
        }
        
        return ans;
    }
}

复杂度分析

  • 时间复杂度: $O(N^2)$。

  • 空间复杂度: $O(N^2)$，其中 $N$ 为 dp 数组的大小。

统计信息

通过次数 提交次数 AC比率
4355 8764 49.7%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言

相似题目

题目 难度
最大正方形 中等
动态规划 数组
上一篇:
763-划分字母区间(Partition Labels)
下一篇:
765-情侣牵手(Couples Holding Hands)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo