原文链接: https://leetcode-cn.com/problems/valid-tic-tac-toe-state

英文原文

Given a Tic-Tac-Toe board as a string array board, return true if and only if it is possible to reach this board position during the course of a valid tic-tac-toe game.

The board is a 3 x 3 array that consists of characters ' ', 'X', and 'O'. The ' ' character represents an empty square.

Here are the rules of Tic-Tac-Toe:

• Players take turns placing characters into empty squares ' '.
• The first player always places 'X' characters, while the second player always places 'O' characters.
• 'X' and 'O' characters are always placed into empty squares, never filled ones.
• The game ends when there are three of the same (non-empty) character filling any row, column, or diagonal.
• The game also ends if all squares are non-empty.
• No more moves can be played if the game is over.

 

Example 1:

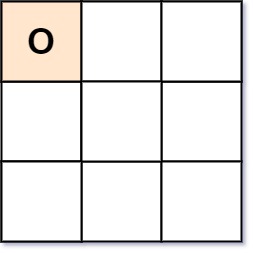
Input: board = ["O  ","   ","   "]
Output: false
Explanation: The first player always plays "X".

Example 2:

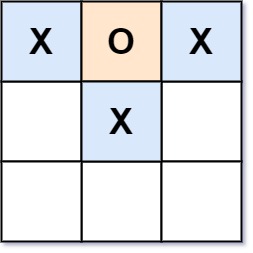
Input: board = ["XOX"," X ","   "]
Output: false
Explanation: Players take turns making moves.

Example 3:

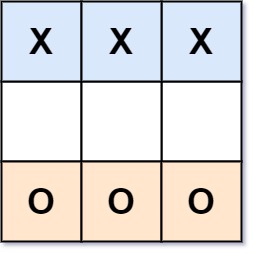
Input: board = ["XXX","   ","OOO"]
Output: false

Example 4:

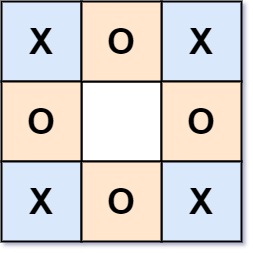
Input: board = ["XOX","O O","XOX"]
Output: true

 

Constraints:

• board.length == 3
• board[i].length == 3
• board[i][j] is either 'X', 'O', or ' '.

中文题目

用字符串数组作为井字游戏的游戏板 board。当且仅当在井字游戏过程中，玩家有可能将字符放置成游戏板所显示的状态时，才返回 true。

该游戏板是一个 3 x 3 数组，由字符 " "，"X" 和 "O" 组成。字符 " " 代表一个空位。

以下是井字游戏的规则：

• 玩家轮流将字符放入空位（" "）中。
• 第一个玩家总是放字符 “X”，且第二个玩家总是放字符 “O”。
• “X” 和 “O” 只允许放置在空位中，不允许对已放有字符的位置进行填充。
• 当有 3 个相同（且非空）的字符填充任何行、列或对角线时，游戏结束。
• 当所有位置非空时，也算为游戏结束。
• 如果游戏结束，玩家不允许再放置字符。

示例 1:
输入: board = ["O  ", "   ", "   "]
输出: false
解释: 第一个玩家总是放置“X”。

示例 2:
输入: board = ["XOX", " X ", "   "]
输出: false
解释: 玩家应该是轮流放置的。

示例 3:
输入: board = ["XXX", "   ", "OOO"]
输出: false

示例 4:
输入: board = ["XOX", "O O", "XOX"]
输出: true

说明:

• 游戏板 board 是长度为 3 的字符串数组，其中每个字符串 board[i] 的长度为 3。
•  board[i][j] 是集合 {" ", "X", "O"} 中的一个字符。

通过代码

官方题解

方法一：分类讨论【通过】

思想

考虑井字游戏板生效的必要条件：

• 因为所有的玩家轮流放棋，所以 X 的数量一定大于等于 O 的数量。

• 获胜的玩家一定是在自己放棋后赢得比赛。

  • 如果第一个玩家获胜，则 X 的数量比 O 的数量多 1。
  • 如果第二个玩家获胜，则 X 的数量与 O 的数量相同。

• 游戏板上不可能同时出现 3 个 X 在一行 和 3 个 O 在另一行。因为一旦有玩家获胜，游戏结束，另外一名玩家不能再放棋。

事实证明，以上条件包含了游戏板生效的全部情况。可以通过反证法验证上面分类条件的正确性。在任何一局比赛中，只能有 3 种结果，要么没有玩家获胜，要么只有一个玩家获胜，要么两个玩家都获胜。在前两种情况下，通过检查两种棋的数量关系即可验证是否有效。最后这一种情况下，不允许两个玩家同时获胜。

算法

统计游戏板上 X 和 O 的数量并记录在 xCount 和 oCount 中。

使用函数 win(player) 检查玩家是否获胜，它检查在棋盘的 3 行，3 列和 2 条对角线上是否有该玩家的连续 3 枚棋子。

[solution1-Java]
class Solution {
    public boolean validTicTacToe(String[] board) {
        int xCount = 0, oCount = 0;
        for (String row: board)
            for (char c: row.toCharArray()) {
                if (c == 'X') xCount++;
                if (c == 'O') oCount++;
            }

        if (oCount != xCount && oCount != xCount - 1) return false;
        if (win(board, 'X') && oCount != xCount - 1) return false;
        if (win(board, 'O') && oCount != xCount) return false;
        return true;
    }

    public boolean win(String[] B, char P) {
        // B: board, P: player
        for (int i = 0; i < 3; ++i) {
            if (P == B[0].charAt(i) && P == B[1].charAt(i) && P == B[2].charAt(i))
                return true;
            if (P == B[i].charAt(0) && P == B[i].charAt(1) && P == B[i].charAt(2))
                return true;
        }
        if (P == B[0].charAt(0) && P == B[1].charAt(1) && P == B[2].charAt(2))
            return true;
        if (P == B[0].charAt(2) && P == B[1].charAt(1) && P == B[2].charAt(0))
            return true;
        return false;
    }
}

[solution1-Python]
class Solution(object):
    def validTicTacToe(self, board):
        FIRST, SECOND = 'XO'
        x_count = sum(row.count(FIRST) for row in board)
        o_count = sum(row.count(SECOND) for row in board)

        def win(board, player):
            for i in xrange(3):
                if all(board[i][j] == player for j in xrange(3)):
                    return True
                if all(board[j][i] == player for j in xrange(3)):
                    return True

            return (player == board[1][1] == board[0][0] == board[2][2] or
                    player == board[1][1] == board[0][2] == board[2][0])

        if o_count not in {x_count-1, x_count}: return False
        if win(board, FIRST) and x_count-1 != o_count: return False
        if win(board, SECOND) and x_count != o_count: return False

        return True

复杂度分析

• 时间和空间复杂度：$O(1)$。

统计信息

通过次数	提交次数	AC比率
7584	22126	34.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
设计井字棋	中等