原文链接: https://leetcode-cn.com/problems/max-increase-to-keep-city-skyline

英文原文

There is a city composed of n x n blocks, where each block contains a single building shaped like a vertical square prism. You are given a 0-indexed n x n integer matrix grid where grid[r][c] represents the height of the building located in the block at row r and column c.

A city's skyline is the the outer contour formed by all the building when viewing the side of the city from a distance. The skyline from each cardinal direction north, east, south, and west may be different.

We are allowed to increase the height of any number of buildings by any amount (the amount can be different per building). The height of a 0-height building can also be increased. However, increasing the height of a building should not affect the city's skyline from any cardinal direction.

Return the maximum total sum that the height of the buildings can be increased by without changing the city's skyline from any cardinal direction.

 

Example 1:

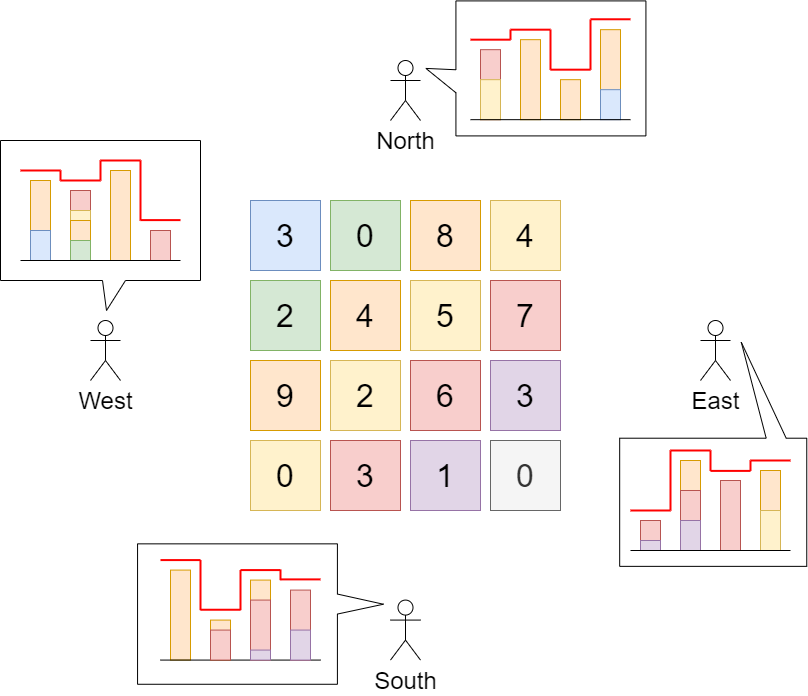
Input: grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
Output: 35
Explanation: The building heights are shown in the center of the above image.
The skylines when viewed from each cardinal direction are drawn in red.
The grid after increasing the height of buildings without affecting skylines is:
gridNew = [ [8, 4, 8, 7],
            [7, 4, 7, 7],
            [9, 4, 8, 7],
            [3, 3, 3, 3] ]

Example 2:

Input: grid = [[0,0,0],[0,0,0],[0,0,0]]
Output: 0
Explanation: Increasing the height of any building will result in the skyline changing.

 

Constraints:

• n == grid.length
• n == grid[r].length
• 2 <= n <= 50
• 0 <= grid[r][c] <= 100

中文题目

在二维数组grid中，grid[i][j]代表位于某处的建筑物的高度。 我们被允许增加任何数量（不同建筑物的数量可能不同）的建筑物的高度。 高度 0 也被认为是建筑物。

最后，从新数组的所有四个方向（即顶部，底部，左侧和右侧）观看的“天际线”必须与原始数组的天际线相同。 城市的天际线是从远处观看时，由所有建筑物形成的矩形的外部轮廓。 请看下面的例子。

建筑物高度可以增加的最大总和是多少？

例子：
输入： grid = [[3,0,8,4],[2,4,5,7],[9,2,6,3],[0,3,1,0]]
输出： 35
解释： 
The grid is:
[ [3, 0, 8, 4], 
  [2, 4, 5, 7],
  [9, 2, 6, 3],
  [0, 3, 1, 0] ]

从数组竖直方向（即顶部，底部）看“天际线”是：[9, 4, 8, 7]
从水平水平方向（即左侧，右侧）看“天际线”是：[8, 7, 9, 3]

在不影响天际线的情况下对建筑物进行增高后，新数组如下：

gridNew = [ [8, 4, 8, 7],
            [7, 4, 7, 7],
            [9, 4, 8, 7],
            [3, 3, 3, 3] ]

说明:

• 1 < grid.length = grid[0].length <= 50。
•  grid[i][j] 的高度范围是： [0, 100]。
• 一座建筑物占据一个grid[i][j]：换言之，它们是 1 x 1 x grid[i][j] 的长方体。

通过代码

官方题解

方法一：计算行列限制

我们首先计算出天际线的值。显然，从顶部和底部看到的天际线是相同的，每一个位置的天际线高度是对应列的建筑物高度最大值，即 col_maxes = [max(column_0), max(column_1), ...]；从左侧和右侧看到的天际线也是相同的，每一个位置的天际线高度是对应行的建筑物高度最大值，即 row_maxes = [max(row_0), max(row_1), ...]。

对于 grid 中的每一个元素，我们可以将它增加到的最大高度为该元素行天际线与列天际线高度的较小值，即 min(row_maxes[r], col_maxes[c])。如果再增加高度，就会导致行天际线或列天际线中的至少一个发生变化。

由于 grid 中的每一个元素的高度增加都是独立的，因此我们贪心地把每一个元素都增加到最大值，就可以得到增加的最大总和。

[sol1]
class Solution {
    public int maxIncreaseKeepingSkyline(int[][] grid) {
        int N = grid.length;
        int[] rowMaxes = new int[N];
        int[] colMaxes = new int[N];

        for (int r = 0; r < N; ++r)
            for (int c = 0; c < N; ++c) {
                rowMaxes[r] = Math.max(rowMaxes[r], grid[r][c]);
                colMaxes[c] = Math.max(colMaxes[c], grid[r][c]);
        }

        int ans = 0;
        for (int r = 0; r < N; ++r)
            for (int c = 0; c < N; ++c)
                ans += Math.min(rowMaxes[r], colMaxes[c]) - grid[r][c];

        return ans;
    }
}

[sol1]
class Solution(object):
    def maxIncreaseKeepingSkyline(self, grid):
        row_maxes = [max(row) for row in grid]
        col_maxes = [max(col) for col in zip(*grid)]

        return sum(min(row_maxes[r], col_maxes[c]) - val
                   for r, row in enumerate(grid)
                   for c, val in enumerate(row))

复杂度分析

• 时间复杂度：$O(N^2)$，其中 $N$ 是 grid 数组的边长。

• 空间复杂度：$O(N)$，用来存储行天际线和列天际线。

统计信息

通过次数	提交次数	AC比率
17241	20363	84.7%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言