原文链接: https://leetcode-cn.com/problems/image-overlap

英文原文

You are given two images, img1 and img2, represented as binary, square matrices of size n x n. A binary matrix has only 0s and 1s as values.

We translate one image however we choose by sliding all the 1 bits left, right, up, and/or down any number of units. We then place it on top of the other image. We can then calculate the overlap by counting the number of positions that have a 1 in both images.

Note also that a translation does not include any kind of rotation. Any 1 bits that are translated outside of the matrix borders are erased.

Return the largest possible overlap.

 

Example 1:

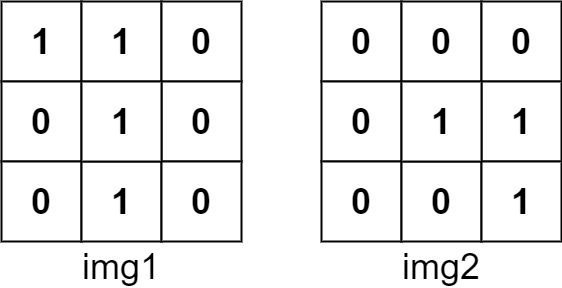
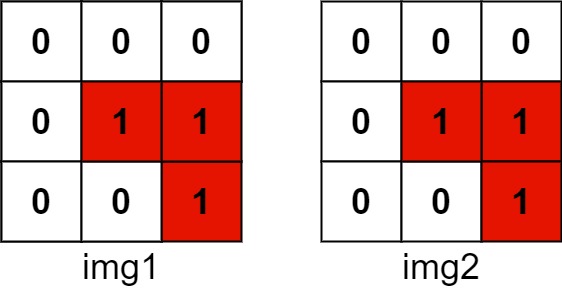
Input: img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
Output: 3
Explanation: We translate img1 to right by 1 unit and down by 1 unit.

The number of positions that have a 1 in both images is 3 (shown in red).

Example 2:

Input: img1 = [[1]], img2 = [[1]]
Output: 1

Example 3:

Input: img1 = [[0]], img2 = [[0]]
Output: 0

 

Constraints:

• n == img1.length == img1[i].length
• n == img2.length == img2[i].length
• 1 <= n <= 30
• img1[i][j] is either 0 or 1.
• img2[i][j] is either 0 or 1.

中文题目

给你两个图像 img1 和 img2 ，两个图像的大小都是 n x n ，用大小相同的二进制正方形矩阵表示。二进制矩阵仅由若干 0 和若干 1 组成。

转换 其中一个图像，将所有的 1 向左，右，上，或下滑动任何数量的单位；然后把它放在另一个图像的上面。该转换的 重叠 是指两个图像 都 具有 1 的位置的数目。

请注意，转换 不包括 向任何方向旋转。越过矩阵边界的 1 都将被清除。

最大可能的重叠数量是多少？

 

示例 1：

输入：img1 = [[1,1,0],[0,1,0],[0,1,0]], img2 = [[0,0,0],[0,1,1],[0,0,1]]
输出：3
解释：将 img1 向右移动 1 个单位，再向下移动 1 个单位。

两个图像都具有 1 的位置的数目是 3（用红色标识）。

示例 2：

输入：img1 = [[1]], img2 = [[1]]
输出：1

示例 3：

输入：img1 = [[0]], img2 = [[0]]
输出：0

 

提示：

• n == img1.length == img1[i].length
• n == img2.length == img2[i].length
• 1 <= n <= 30
• img1[i][j] 为 0 或 1
• img2[i][j] 为 0 或 1

通过代码

官方题解

方法一：枚举偏移量并计数

我们用二元组 (x, y) 表示对 A 的偏移量 delta，其中 x 表示向左（负数）或向右（正数），y 表示向上（负数）或向下（正数）。在枚举偏移量时，我们可以分别枚举 A 和 B 中的一个 1，此时 delta 即为 A 中的 1 到 B 中的 1 的偏移量。枚举偏移量的时间复杂度为 $O(N^4)$。随后，我们对于 A 中的每个位置，判断它经过偏移后在 B 中的位置是否为 1。这一步的时间复杂度为 $O(N^2)$。

为了方便维护偏移量 delta，我们可以用 Java 中的 java.awt.Point 或者 Python 中的 complex 来表示偏移量。在优化方面，我们可以在枚举了 delta 之后进行记录，如果下一次枚举到了同样的 delta，就可以跳过并减少一次 $O(N^2)$ 的判断计算。这样做可以减少一定的运行时间，但不会降低时间复杂度。

[sol1]
import java.awt.Point;

class Solution {
    public int largestOverlap(int[][] A, int[][] B) {
        int N = A.length;
        List<Point> A2 = new ArrayList(), B2 = new ArrayList();
        for (int i = 0; i < N*N; ++i) {
            if (A[i/N][i%N] == 1) A2.add(new Point(i/N, i%N));
            if (B[i/N][i%N] == 1) B2.add(new Point(i/N, i%N));
        }

        Set<Point> Bset = new HashSet(B2);

        int ans = 0;
        Set<Point> seen = new HashSet();
        for (Point a: A2) for (Point b: B2) {
            Point delta = new Point(b.x - a.x, b.y - a.y);
            if (!seen.contains(delta)) {
                seen.add(delta);
                int cand = 0;
                for (Point p: A2)
                    if (Bset.contains(new Point(p.x + delta.x, p.y + delta.y)))
                        cand++;
                ans = Math.max(ans, cand);
            }
        }

        return ans;
    }
}

[sol1]
class Solution(object):
    def largestOverlap(self, A, B):
        N = len(A)
        A2 = [complex(r, c) for r, row in enumerate(A)
              for c, v in enumerate(row) if v]
        B2 = [complex(r, c) for r, row in enumerate(B)
              for c, v in enumerate(row) if v]
        Bset = set(B2)
        seen = set()
        ans = 0
        for a in A2:
            for b in B2:
                d = b-a
                if d not in seen:
                    seen.add(d)
                    ans = max(ans, sum(x+d in Bset for x in A2))
        return ans

复杂度分析

• 时间复杂度：$O(N^6)$，其中 $N$ 是数组 A 和 B 的边长。

• 空间复杂度：$O(N^2)$。

方法二：直接对偏移量计数

我们反向思考方法一，就可以得到一种新的方法。我们分别枚举 A 和 B 中的一个 1，计算出偏移量 delta 并放入计数器中。对于每一个 delta，如果它在计数器中出现了 k 次，那么偏移量为 delta 时，A 和 B 重合的 1 的数目就为 k。

[sol2]
class Solution {
    public int largestOverlap(int[][] A, int[][] B) {
        int N = A.length;
        int[][] count = new int[2*N+1][2*N+1];
        for (int i = 0; i < N; ++i)
            for (int j = 0; j < N; ++j)
                if (A[i][j] == 1)
                    for (int i2 = 0; i2 < N; ++i2)
                        for (int j2 = 0; j2 < N; ++j2)
                            if (B[i2][j2] == 1)
                                count[i-i2 +N][j-j2 +N] += 1;

        int ans = 0;
        for (int[] row: count)
            for (int v: row)
                ans = Math.max(ans, v);
        return ans;
    }
}

[sol2]
class Solution(object):
    def largestOverlap(self, A, B):
        N = len(A)
        count = collections.Counter()
        for i, row in enumerate(A):
            for j, v in enumerate(row):
                if v:
                    for i2, row2 in enumerate(B):
                        for j2, v2 in enumerate(row2):
                            if v2:
                                count[i-i2, j-j2] += 1
        return max(count.values() or [0])

复杂度分析

• 时间复杂度：$O(N^4)$，其中 $N$ 是数组 A 和 B 的边长。

• 空间复杂度：$O(N^2)$。

统计信息

通过次数	提交次数	AC比率
4460	7752	57.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言