原文链接: https://leetcode-cn.com/problems/maximize-distance-to-closest-person

英文原文

You are given an array representing a row of seats where seats[i] = 1 represents a person sitting in the ith seat, and seats[i] = 0 represents that the ith seat is empty (0-indexed).

There is at least one empty seat, and at least one person sitting.

Alex wants to sit in the seat such that the distance between him and the closest person to him is maximized. 

Return that maximum distance to the closest person.

 

Example 1:

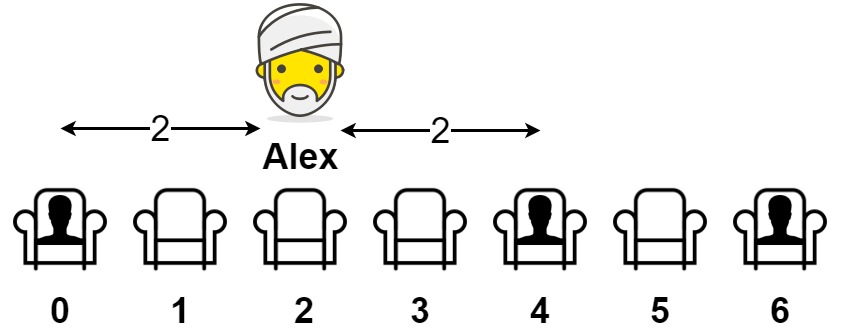
Input: seats = [1,0,0,0,1,0,1]
Output: 2
Explanation: 
If Alex sits in the second open seat (i.e. seats[2]), then the closest person has distance 2.
If Alex sits in any other open seat, the closest person has distance 1.
Thus, the maximum distance to the closest person is 2.

Example 2:

Input: seats = [1,0,0,0]
Output: 3
Explanation: 
If Alex sits in the last seat (i.e. seats[3]), the closest person is 3 seats away.
This is the maximum distance possible, so the answer is 3.

Example 3:

Input: seats = [0,1]
Output: 1

 

Constraints:

• 2 <= seats.length <= 2 * 104
• seats[i] is 0 or 1.
• At least one seat is empty.
• At least one seat is occupied.

中文题目

给你一个数组 seats 表示一排座位，其中 seats[i] = 1 代表有人坐在第 i 个座位上，seats[i] = 0 代表座位 i 上是空的（下标从 0 开始）。

至少有一个空座位，且至少有一人已经坐在座位上。

亚历克斯希望坐在一个能够使他与离他最近的人之间的距离达到最大化的座位上。

返回他到离他最近的人的最大距离。

 

示例 1：

输入：seats = [1,0,0,0,1,0,1]
输出：2
解释：
如果亚历克斯坐在第二个空位（seats[2]）上，他到离他最近的人的距离为 2 。
如果亚历克斯坐在其它任何一个空位上，他到离他最近的人的距离为 1 。
因此，他到离他最近的人的最大距离是 2 。 

示例 2：

输入：seats = [1,0,0,0]
输出：3
解释：
如果亚历克斯坐在最后一个座位上，他离最近的人有 3 个座位远。
这是可能的最大距离，所以答案是 3 。

示例 3：

输入：seats = [0,1]
输出：1

 

提示：

• 2 <= seats.length <= 2 * 104
• seats[i] 为 0 或 1
• 至少有一个 空座位
• 至少有一个 座位上有人

通过代码

官方题解

方法一：计算座位到最近的人的最大距离【通过】

思路

令 left[i] 为座位 i 到坐在 i 左边的人的最近距离。同理 right[i] 为座位 i 到坐在 i 右边的人的最近距离。那么该座位到最近的人的距离为 min(left[i], right[i])。

算法

如果 i 左边的位置是空的，那么 left[i] = left[i - 1] + 1；否则 left[i] = 0。right[i] 的计算方法类似。

[solution1-Java]
class Solution {
    public int maxDistToClosest(int[] seats) {
        int N = seats.length;
        int[] left = new int[N], right = new int[N];
        Arrays.fill(left, N);
        Arrays.fill(right, N);

        for (int i = 0; i < N; ++i) {
            if (seats[i] == 1) left[i] = 0;
            else if (i > 0) left[i] = left[i-1] + 1;
        }

        for (int i = N-1; i >= 0; --i) {
            if (seats[i] == 1) right[i] = 0;
            else if (i < N-1) right[i] = right[i+1] + 1;
        }

        int ans = 0;
        for (int i = 0; i < N; ++i)
            if (seats[i] == 0)
                ans = Math.max(ans, Math.min(left[i], right[i]));
        return ans;
    }
}

[solution1-Python]
class Solution(object):
    def maxDistToClosest(self, seats):
        N = len(seats)
        left, right = [N] * N, [N] * N

        for i in xrange(N):
            if seats[i] == 1: left[i] = 0
            elif i > 0: left[i] = left[i-1] + 1

        for i in xrange(N-1, -1, -1):
            if seats[i] == 1: right[i] = 0
            elif i < N-1: right[i] = right[i+1] + 1

        return max(min(left[i], right[i])
                   for i, seat in enumerate(seats) if not seat)

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是 seats 的长度。

• 空间复杂度：$O(N)$，存储 left 和 right 的空间。

方法二：双指针【通过】

思路

遍历所有座位 seats，找出每个空位左边最近的人和右边最近的人，更新当前空位到最近的人的距离。

算法

使用 prev 记录 i 最左边第一个有人的位置，future 记录 i 最右边第一个有人的位置。

座位 i 到最近的人的距离为 min(i - prev, future - i)。另外有一种特殊情况，如果座位 i 左边没有人，则认为到左边第一个人的距离是无限大，右边同理。

[solution2-Java]
class Solution {
    public int maxDistToClosest(int[] seats) {
        int N = seats.length;
        int prev = -1, future = 0;
        int ans = 0;

        for (int i = 0; i < N; ++i) {
            if (seats[i] == 1) {
                prev = i;
            } else {
                while (future < N && seats[future] == 0 || future < i)
                    future++;

                int left = prev == -1 ? N : i - prev;
                int right = future == N ? N : future - i;
                ans = Math.max(ans, Math.min(left, right));
            }
        }

        return ans;
    }
}

[solution2-Python]
class Solution(object):
    def maxDistToClosest(self, seats):
        people = (i for i, seat in enumerate(seats) if seat)
        prev, future = None, next(people)

        ans = 0
        for i, seat in enumerate(seats):
            if seat:
                prev = i
            else:
                while future is not None and future < i:
                    future = next(people, None)

                left = float('inf') if prev is None else i - prev
                right = float('inf') if future is None else future - i
                ans = max(ans, min(left, right))

        return ans

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是 seats 的长度。

• 空间复杂度：$O(1)$。

方法三：按零分组【通过】

思路

如果两人之间有连续 K 个空座位，那么其中存在至少一个座位到两边最近的人的距离为 (K+1) / 2。

算法

假设两个人之间有 K 个空座位，则存在座位到最近的人的距离为 (K+1) / 2。

对于边缘的座位，它们的一侧没有人，那么认为它们到该侧最近的人的距离为 K。

[solution3-Java]
class Solution {
    public int maxDistToClosest(int[] seats) {
        int N = seats.length;
        int K = 0; //current longest group of empty seats
        int ans = 0;

        for (int i = 0; i < N; ++i) {
            if (seats[i] == 1) {
                K = 0;
            } else {
                K++;
                ans = Math.max(ans, (K + 1) / 2);
            }
        }

        for (int i = 0; i < N; ++i)  if (seats[i] == 1) {
            ans = Math.max(ans, i);
            break;
        }

        for (int i = N-1; i >= 0; --i)  if (seats[i] == 1) {
            ans = Math.max(ans, N - 1 - i);
            break;
        }

        return ans;
    }
}

[solution3-Python]
class Solution(object):
    def maxDistToClosest(self, seats):
        ans = 0
        for seat, group in itertools.groupby(seats):
            if not seat:
                K = len(list(group))
                ans = max(ans, (K+1)/2)

        return max(ans, seats.index(1), seats[::-1].index(1))

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是 seats 的长度。

• 空间复杂度：$O(1)$。在 Python中 seats[::-1] 的空间为 $O(N)$，但它可以被省略。

统计信息

通过次数	提交次数	AC比率
16462	38472	42.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
考场就座	中等