原文链接: https://leetcode-cn.com/problems/score-after-flipping-matrix

英文原文

You are given an m x n binary matrix grid.

A move consists of choosing any row or column and toggling each value in that row or column (i.e., changing all 0's to 1's, and all 1's to 0's).

Every row of the matrix is interpreted as a binary number, and the score of the matrix is the sum of these numbers.

Return the highest possible score after making any number of moves (including zero moves).

 

Example 1:

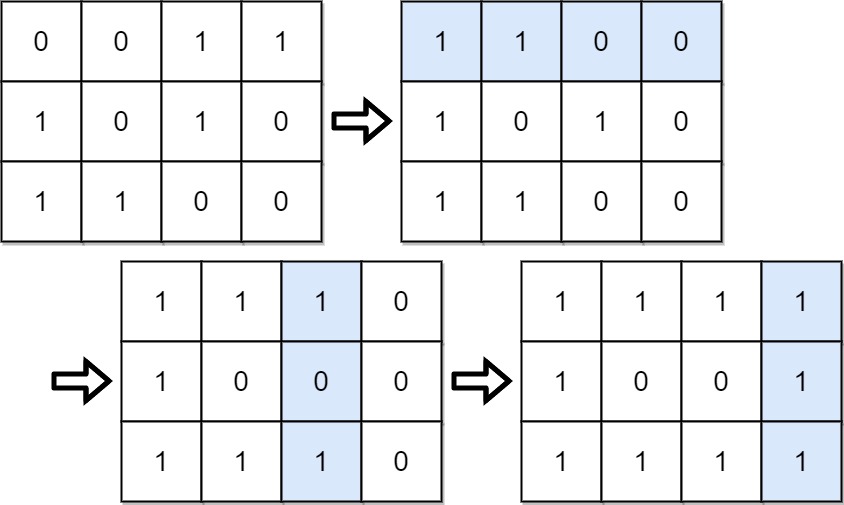
Input: grid = [[0,0,1,1],[1,0,1,0],[1,1,0,0]]
Output: 39
Explanation: 0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

Example 2:

Input: grid = [[0]]
Output: 1

 

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 20
• grid[i][j] is either 0 or 1.

中文题目

有一个二维矩阵 A 其中每个元素的值为 0 或 1 。

移动是指选择任一行或列，并转换该行或列中的每一个值：将所有 0 都更改为 1，将所有 1 都更改为 0。

在做出任意次数的移动后，将该矩阵的每一行都按照二进制数来解释，矩阵的得分就是这些数字的总和。

返回尽可能高的分数。

 

示例：

输入：[[0,0,1,1],[1,0,1,0],[1,1,0,0]]
输出：39
解释：
转换为 [[1,1,1,1],[1,0,0,1],[1,1,1,1]]
0b1111 + 0b1001 + 0b1111 = 15 + 9 + 15 = 39

 

提示：

1. 1 <= A.length <= 20
2. 1 <= A[0].length <= 20
3. A[i][j] 是 0 或 1

通过代码

高赞题解

方法一：贪心

根据题意，能够知道一个重要的事实：给定一个翻转方案，则它们之间任意交换顺序后，得到的结果保持不变。因此，我们总可以先考虑所有的行翻转，再考虑所有的列翻转。

不难发现一点：为了得到最高的分数，矩阵的每一行的最左边的数都必须为 $1$。为了做到这一点，我们可以翻转那些最左边的数不为 $1$ 的那些行，而其他的行则保持不动。

当将每一行的最左边的数都变为 $1$ 之后，就只能进行列翻转了。为了使得总得分最大，我们要让每个列中 $1$ 的数目尽可能多。因此，我们扫描除了最左边的列以外的每一列，如果该列 $0$ 的数目多于 $1$ 的数目，就翻转该列，其他的列则保持不变。

实际编写代码时，我们无需修改原矩阵，而是可以计算每一列对总分数的「贡献」，从而直接计算出最高的分数。假设矩阵共有 $m$ 行 $n$ 列，计算方法如下：

• 对于最左边的列而言，由于最优情况下，它们的取值都为 $1$，因此每个元素对分数的贡献都为 $2^{n-1}$，总贡献为 $m \times 2^{n-1}$。

• 对于第 $j$ 列（$j>0$，此处规定最左边的列是第 $0$ 列）而言，我们统计这一列 $0,1$ 的数量，令其中的最大值为 $k$，则 $k$ 是列翻转后的 $1$ 的数量，该列的总贡献为 $k \times 2^{n-j-1}$。需要注意的是，在统计 $0,1$ 的数量的时候，要考虑最初进行的行反转。

[sol1-C++]
class Solution {
public:
    int matrixScore(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        int ret = m * (1 << (n - 1));

        for (int j = 1; j < n; j++) {
            int nOnes = 0;
            for (int i = 0; i < m; i++) {
                if (grid[i][0] == 1) {
                    nOnes += grid[i][j];
                } else {
                    nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
                }
            }
            int k = max(nOnes, m - nOnes);
            ret += k * (1 << (n - j - 1));
        }
        return ret;
    }
};

[sol1-Java]
class Solution {
    public int matrixScore(int[][] grid) {
        int m = grid.length, n = grid[0].length;
        int ret = m * (1 << (n - 1));

        for (int j = 1; j < n; j++) {
            int nOnes = 0;
            for (int i = 0; i < m; i++) {
                if (grid[i][0] == 1) {
                    nOnes += grid[i][j];
                } else {
                    nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
                }
            }
            int k = Math.max(nOnes, m - nOnes);
            ret += k * (1 << (n - j - 1));
        }
        return ret;
    }
}

[sol1-Golang]
func matrixScore(grid [][]int) int {
    m, n := len(grid), len(grid[0])
    ans := 1 << (n - 1) * m
    for j := 1; j < n; j++ {
        ones := 0
        for _, row := range grid {
            if row[j] == row[0] {
                ones++
            }
        }
        if ones < m-ones {
            ones = m - ones
        }
        ans += 1 << (n - 1 - j) * ones
    }
    return ans
}

[sol1-JavaScript]
var matrixScore = function(grid) {
    const m = grid.length, n = grid[0].length;
    let ret = m * (1 << (n - 1));

    for (let j = 1; j < n; j++) {
        let nOnes = 0;
        for (let i = 0; i < m; i++) {
            if (grid[i][0] === 1) {
                nOnes += grid[i][j];
            } else {
                nOnes += (1 - grid[i][j]); // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
            }
        }
        const k = Math.max(nOnes, m - nOnes);
        ret += k * (1 << (n - j - 1));
    }
    return ret;
};

[sol1-C]
int matrixScore(int** grid, int gridSize, int* gridColSize) {
    int m = gridSize, n = gridColSize[0];
    int ret = m * (1 << (n - 1));

    for (int j = 1; j < n; j++) {
        int nOnes = 0;
        for (int i = 0; i < m; i++) {
            if (grid[i][0] == 1) {
                nOnes += grid[i][j];
            } else {
                nOnes += (1 - grid[i][j]);  // 如果这一行进行了行反转，则该元素的实际取值为 1 - grid[i][j]
            }
        }
        int k = fmax(nOnes, m - nOnes);
        ret += k * (1 << (n - j - 1));
    }
    return ret;
}

复杂度分析

• 时间复杂度：$O(mn)$，其中 $m$ 为矩阵行数，$n$ 为矩阵列数。

• 空间复杂度：$O(1)$。

统计信息

通过次数	提交次数	AC比率
31906	39429	80.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言