原文链接: https://leetcode-cn.com/problems/all-nodes-distance-k-in-binary-tree

英文原文

Given the root of a binary tree, the value of a target node target, and an integer k, return an array of the values of all nodes that have a distance k from the target node.

You can return the answer in any order.

 

Example 1:

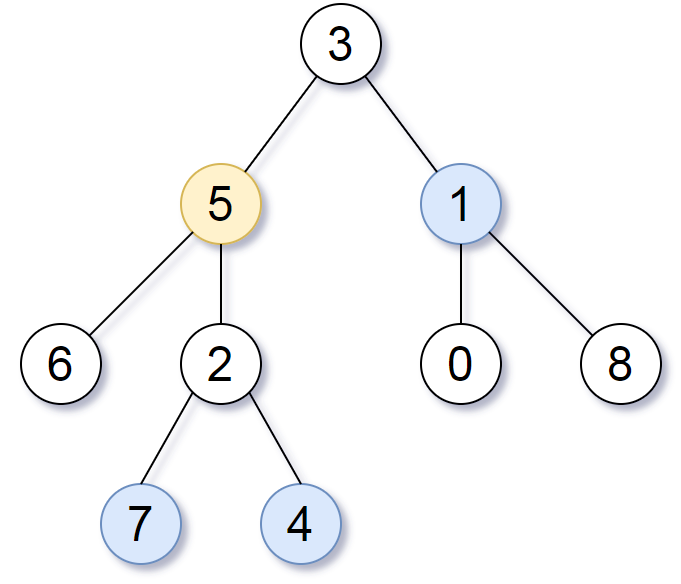
Input: root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, k = 2
Output: [7,4,1]
Explanation: The nodes that are a distance 2 from the target node (with value 5) have values 7, 4, and 1.

Example 2:

Input: root = [1], target = 1, k = 3
Output: []

 

Constraints:

• The number of nodes in the tree is in the range [1, 500].
• 0 <= Node.val <= 500
• All the values Node.val are unique.
• target is the value of one of the nodes in the tree.
• 0 <= k <= 1000

中文题目

给定一个二叉树（具有根结点 root）， 一个目标结点 target ，和一个整数值 K 。

返回到目标结点 target 距离为 K 的所有结点的值的列表。 答案可以以任何顺序返回。

 

示例 1：

输入：root = [3,5,1,6,2,0,8,null,null,7,4], target = 5, K = 2
输出：[7,4,1]
解释：
所求结点为与目标结点（值为 5）距离为 2 的结点，
值分别为 7，4，以及 1



注意，输入的 "root" 和 "target" 实际上是树上的结点。
上面的输入仅仅是对这些对象进行了序列化描述。

 

提示：

1. 给定的树是非空的。
2. 树上的每个结点都具有唯一的值 0 <= node.val <= 500 。
3. 目标结点 target 是树上的结点。
4. 0 <= K <= 1000.

通过代码

高赞题解

基本分析

显然，如果题目是以图的形式给出的话，我们可以很容易通过「BFS / 迭代加深」找到距离为 $k$ 的节点集。

而树是一类特殊的图，我们可以通过将二叉树转换为图的形式，再进行「BFS / 迭代加深」。

由于二叉树每个点最多有 $2$ 个子节点，点和边的数量接近，属于稀疏图，因此我们可以使用「邻接表」的形式进行存储。

建图方式为：对于二叉树中相互连通的节点（root 与 root.left、root 和 root.right），建立一条无向边。

建图需要遍历整棵树，使用 DFS 或者 BFS 均可。

由于所有边的权重均为 $1$，我们可以使用 「BFS / 迭代加深」 找到从目标节点 target 出发，与目标节点距离为 $k$ 的节点，然后将其添加到答案中。

一些细节：利用每个节点具有唯一的值，我们可以直接使用节点值进行建图和搜索。

---

建图 + BFS

由「基本分析」，可写出「建图 + BFS」的实现。

代码：

[]
class Solution {
    // 根据数据范围最多有 501 个点，每个点最多有 2 条无向边（两个子节点）
    int N = 510, M = N * 4;
    int[] he = new int[N], e = new int[M], ne = new int[M];
    int idx;
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = he[a];
        he[a] = idx++;
    }
    boolean[] vis = new boolean[N];
    public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
        List<Integer> ans = new ArrayList<>();
        Arrays.fill(he, -1);
        dfs(root);
        Deque<Integer> d = new ArrayDeque<>();
        d.addLast(t.val);
        vis[t.val] = true;
        while (!d.isEmpty() && k >= 0) {
            int size = d.size();
            while (size-- > 0) {
                int poll = d.pollFirst();
                if (k == 0) {
                    ans.add(poll);
                    continue;
                }
                for (int i = he[poll]; i != -1 ; i = ne[i]) {
                    int j = e[i];
                    if (!vis[j]) {
                        d.addLast(j);
                        vis[j] = true;
                    }
                }
            }
            k--;
        }
        return ans;
    }
    void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }
}

• 时间复杂度：通过 DFS 进行建图的复杂度为 $O(n)$；通过 BFS 找到距离 $target$ 为 $k$ 的节点，复杂度为 $O(n)$。整体复杂度为 $O(n)$
• 空间复杂度：因为是二叉树，边数与点数是呈线性关系。复杂度为 $O(n)$

---

建图 + 迭代加深

由「基本分析」，可写出「建图 + 迭代加深」的实现。

迭代加深的形式，我们只需要结合题意，搜索深度为 $k$ 的这一层即可。

代码：

[]
class Solution {
    // 根据数据范围最多有 501 个点，每个点最多有 2 条无向边（两个子节点）
    int N = 510, M = N * 4;
    int[] he = new int[N], e = new int[M], ne = new int[M];
    int idx;
    void add(int a, int b) {
        e[idx] = b;
        ne[idx] = he[a];
        he[a] = idx++;
    }
    boolean[] vis = new boolean[N];
    public List<Integer> distanceK(TreeNode root, TreeNode t, int k) {
        List<Integer> ans = new ArrayList<>();
        Arrays.fill(he, -1);
        dfs(root);
        vis[t.val] = true;
        find(t.val, k, 0, ans);
        return ans;
    }
    void find(int root, int max, int cur, List<Integer> ans) {
        if (cur == max) {
            ans.add(root);
            return ;
        }
        for (int i = he[root]; i != -1; i = ne[i]) {
            int j = e[i];
            if (!vis[j]) {
                vis[j] = true;
                find(j, max, cur + 1, ans);
            }
        }
    }
    void dfs(TreeNode root) {
        if (root == null) return;
        if (root.left != null) {
            add(root.val, root.left.val);
            add(root.left.val, root.val);
            dfs(root.left);
        }
        if (root.right != null) {
            add(root.val, root.right.val);
            add(root.right.val, root.val);
            dfs(root.right);
        }
    }
}

• 时间复杂度：通过 DFS 进行建图的复杂度为 $O(n)$；通过迭代加深找到距离 $target$ 为 $k$ 的节点，复杂度为 $O(n)$。整体复杂度为 $O(n)$
• 空间复杂度：因为是二叉树，边数与点数是呈线性关系。复杂度为 $O(n)$

---

答疑

评论区不少小伙伴对 add 的存图方式有疑问，这里集中回答一下 ~

这是一种在图论中十分常见的存图方式，可直接当作模板进行背过，与数组存储单链表的实现一致。

首先 idx 是用来对边进行编号的，然后对存图用到的几个数组作简单解释：

• he 数组：存储是某个节点所对应的边的集合（链表）的头结点；
• e 数组：由于访问某一条边指向的节点；
• ne 数组：由于是以链表的形式进行存边，该数组就是用于找到下一条边。

因此当我们想要遍历所有由 a 点发出的边时，可以使用如下方式：

[]
for (int i = he[a]; i != -1; i = ne[i]) {
    int j = e[i]; // 存在由 a 指向 j 的边
}

另外，在评论区 @Meteordream 小姐姐给出了很好的解释：

数组 he 的下标表示结点，值是一个索引 ind，e[ind] 表示 对应一条边，ne[ind] 表示下一个连接结点的索引，假设与 结点a 相连的结点有 b, c, 那么通过 he[a]取得一个索引 ind1 后，通过 e[ind1] = b 可以得到与 a 相连的第一个结点是 b，然后通过 ne[ind1] 可以获得下一个结点的索引 ind2 ，通过 e[ind2] = c 可以得到与 a 相连的第二个结点是 c，最后 ne[ind2] = -1 说明没有下一个结点了
add函数采用链表的头插法，假设 结点a 已经有一个相连的结点 b，那么就有 he[a]=ind, e[ind]=b ，此时再给 a 增加一个相连的结点 c，那么就要建立由b的索引到新结点c的索引 ne[new_ind] = he[a] = ind ，然后新建一条边 e[new_ind], 最后更新 he[a] = new_ind ，就完成了由 a -> b 到 a -> c -> b 的添加操作
可以理解为 he 是邻接表的表头，key是结点val是一个指向存有相邻结点的链表头指针，e是链表结点的val即相邻结点，ne是链表结点的next指针

如果还有疑问的小伙伴，可以带着「链式前向星存图」关键字进行搜索学习哦 ~

---

最后

如果有帮助到你，请给题解点个赞和收藏，让更多的人看到 ~ (“▔□▔)/

也欢迎你 关注我（公主号后台回复「送书」即可参与看题解学算法送实体书长期活动）或 加入「组队打卡」小群 ，提供写「证明」&「思路」的高质量题解。

所有题解已经加入 刷题指南，欢迎 star 哦 ~

统计信息

通过次数	提交次数	AC比率
36819	60872	60.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言