877-石子游戏(Stone Game)
发表于：2021-12-03 | 分类： 中等
字数统计: 593 | 阅读时长: 2分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/stone-game

英文原文

Alice and Bob play a game with piles of stones. There are an even number of piles arranged in a row, and each pile has a positive integer number of stones piles[i].

The objective of the game is to end with the most stones. The total number of stones across all the piles is odd, so there are no ties.

Alice and Bob take turns, with Alice starting first. Each turn, a player takes the entire pile of stones either from the beginning or from the end of the row. This continues until there are no more piles left, at which point the person with the most stones wins.

Assuming Alice and Bob play optimally, return true if Alice wins the game, or false if Bob wins.

 

Example 1:

Input: piles = [5,3,4,5]
Output: true
Explanation: 
Alice starts first, and can only take the first 5 or the last 5.
Say she takes the first 5, so that the row becomes [3, 4, 5].
If Bob takes 3, then the board is [4, 5], and Alice takes 5 to win with 10 points.
If Bob takes the last 5, then the board is [3, 4], and Alice takes 4 to win with 9 points.
This demonstrated that taking the first 5 was a winning move for Alice, so we return true.

Example 2:

Input: piles = [3,7,2,3]
Output: true

 

Constraints:

  • 2 <= piles.length <= 500
  • piles.length is even.
  • 1 <= piles[i] <= 500
  • sum(piles[i]) is odd.

中文题目

亚历克斯和李用几堆石子在做游戏。偶数堆石子排成一行，每堆都有正整数颗石子 piles[i] 。

游戏以谁手中的石子最多来决出胜负。石子的总数是奇数，所以没有平局。

亚历克斯和李轮流进行，亚历克斯先开始。 每回合，玩家从行的开始或结束处取走整堆石头。 这种情况一直持续到没有更多的石子堆为止，此时手中石子最多的玩家获胜。

假设亚历克斯和李都发挥出最佳水平，当亚历克斯赢得比赛时返回 true ，当李赢得比赛时返回 false 。

 

示例：

输入：[5,3,4,5]
输出：true
解释：
亚历克斯先开始，只能拿前 5 颗或后 5 颗石子 。
假设他取了前 5 颗，这一行就变成了 [3,4,5] 。
如果李拿走前 3 颗，那么剩下的是 [4,5]，亚历克斯拿走后 5 颗赢得 10 分。
如果李拿走后 5 颗，那么剩下的是 [3,4]，亚历克斯拿走后 4 颗赢得 9 分。
这表明，取前 5 颗石子对亚历克斯来说是一个胜利的举动，所以我们返回 true 。

 

提示：

  • 2 <= piles.length <= 500
  • piles.length 是偶数。
  • 1 <= piles[i] <= 500
  • sum(piles) 是奇数。

通过代码

高赞题解

前言

这道题是「486. 预测赢家」的特例。和第 486 题相比，这道题增加了两个限制条件：

  • 数组的长度是偶数；

  • 数组的元素之和是奇数，所以没有平局。

这道题可以使用第 486 题的解法进行求解。如果充分利用上述两个限制条件，还可以使用数学方法进行求解。

方法一：动态规划

由于每次只能从行的开始或结束处取走整堆石子，因此可以保证剩下的石子堆一定是连续的。

如果只剩下一堆石子，则当前玩家只能取走这堆石子。如果剩下多堆石子，则当前玩家可以选择从行的开始或结束处取走整堆石子，然后轮到另一个玩家在剩下的石子堆中取走石子。这是一个递归的过程，因此可以使用递归进行求解，递归过程中维护一个总数，表示 $\text{Alice}$ 和 $\text{Bob}$ 的石子数量之差，当游戏结束时，如果总数大于 $0$，则 $\text{Alice}$ 赢得比赛，否则 $\text{Bob}$ 赢得比赛。

如果有 $n$ 堆石子，则递归的时间复杂度为 $O(2^n)$，无法通过所有的测试用例。递归的时间复杂度高的原因是存在大量重复计算。由于存在重复子问题，因此可以使用动态规划降低时间复杂度。

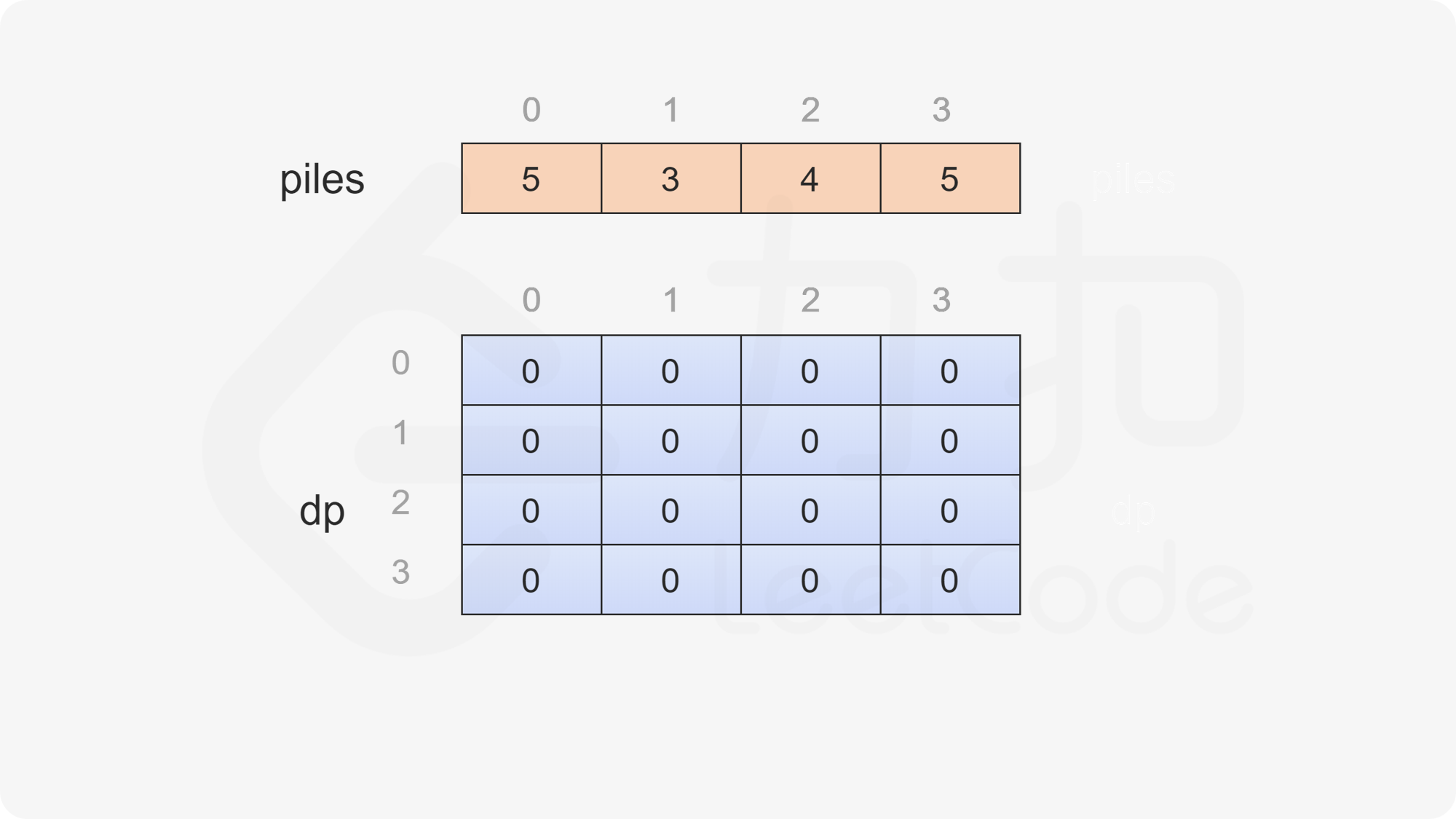
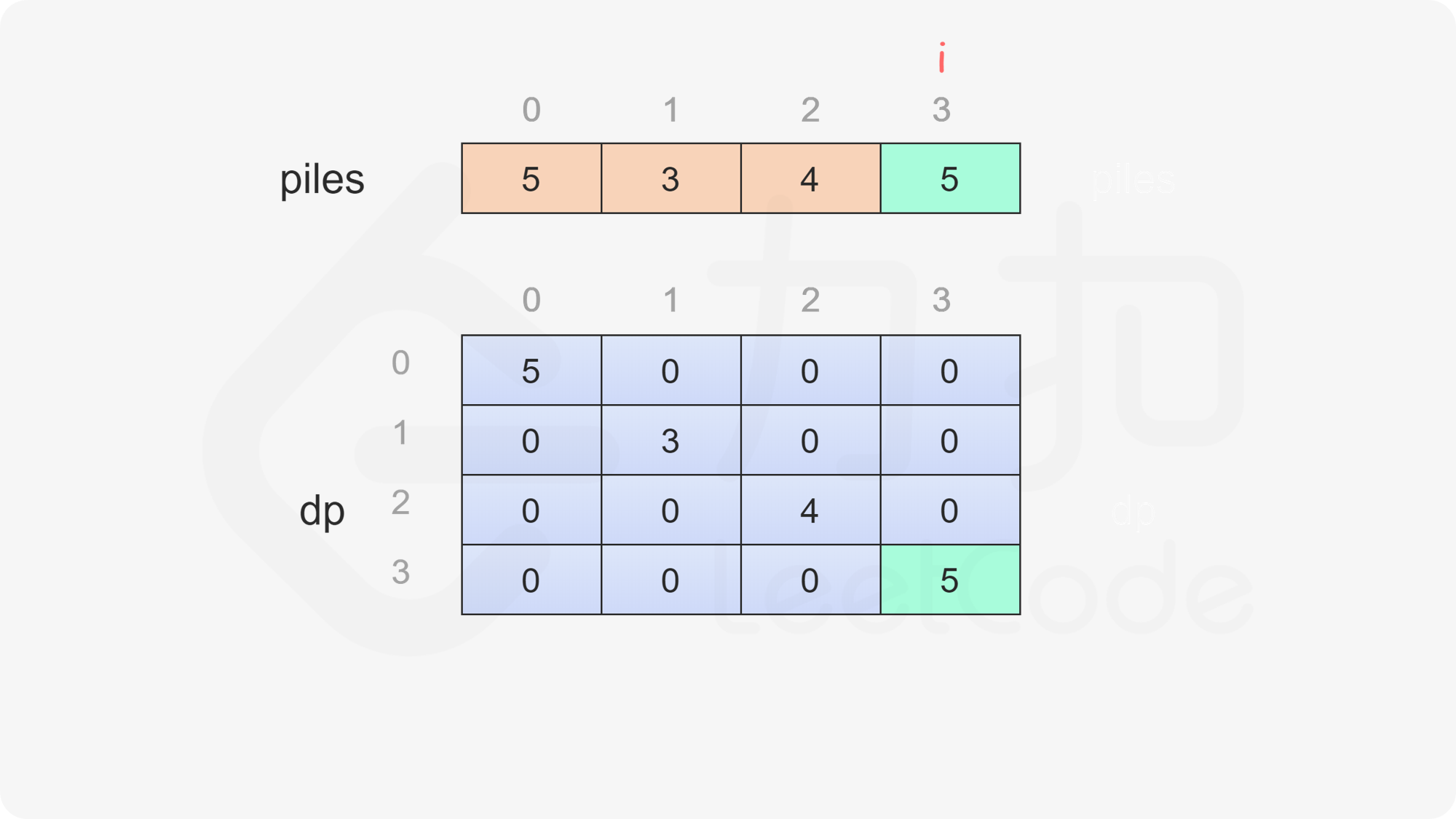
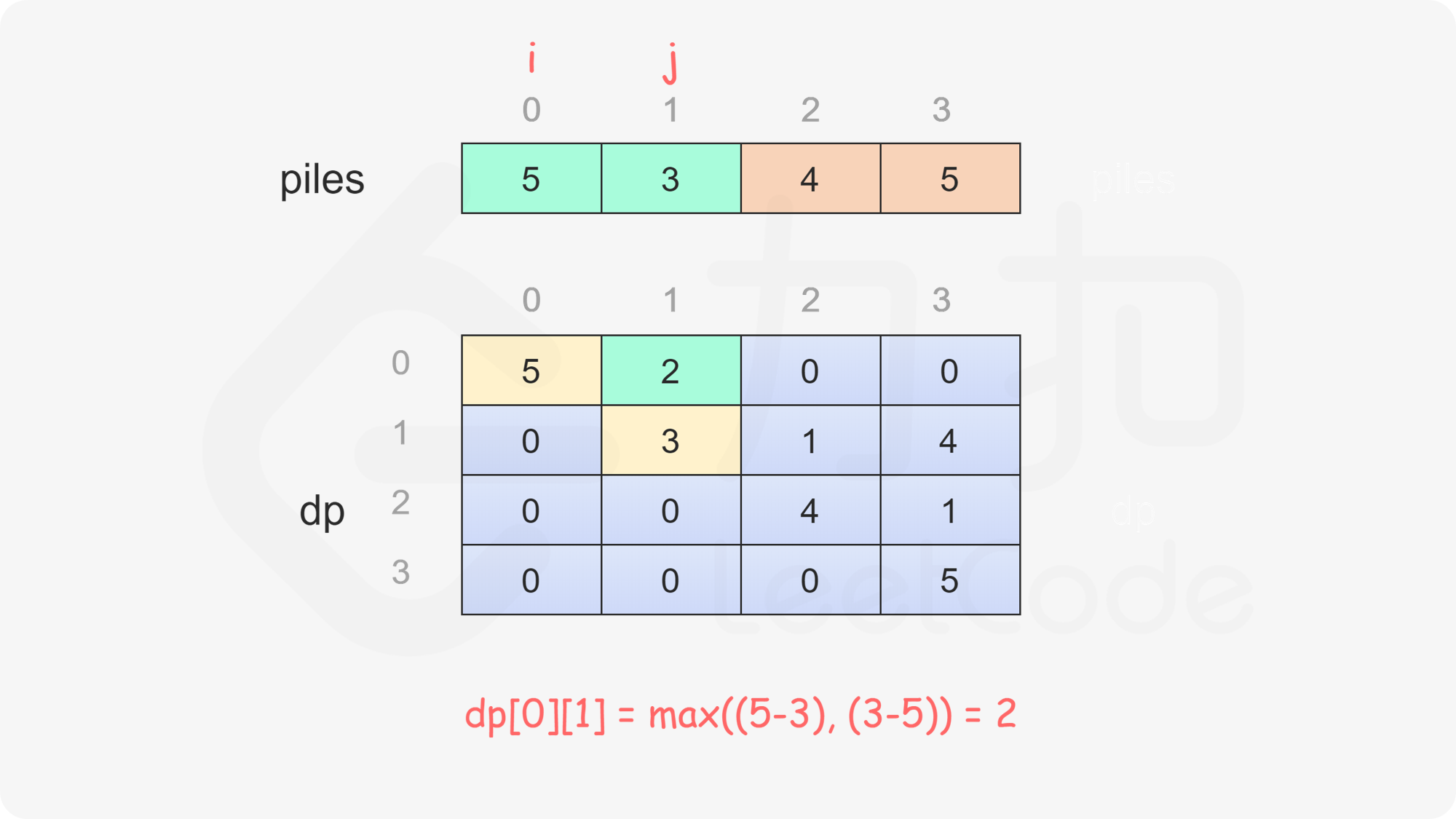
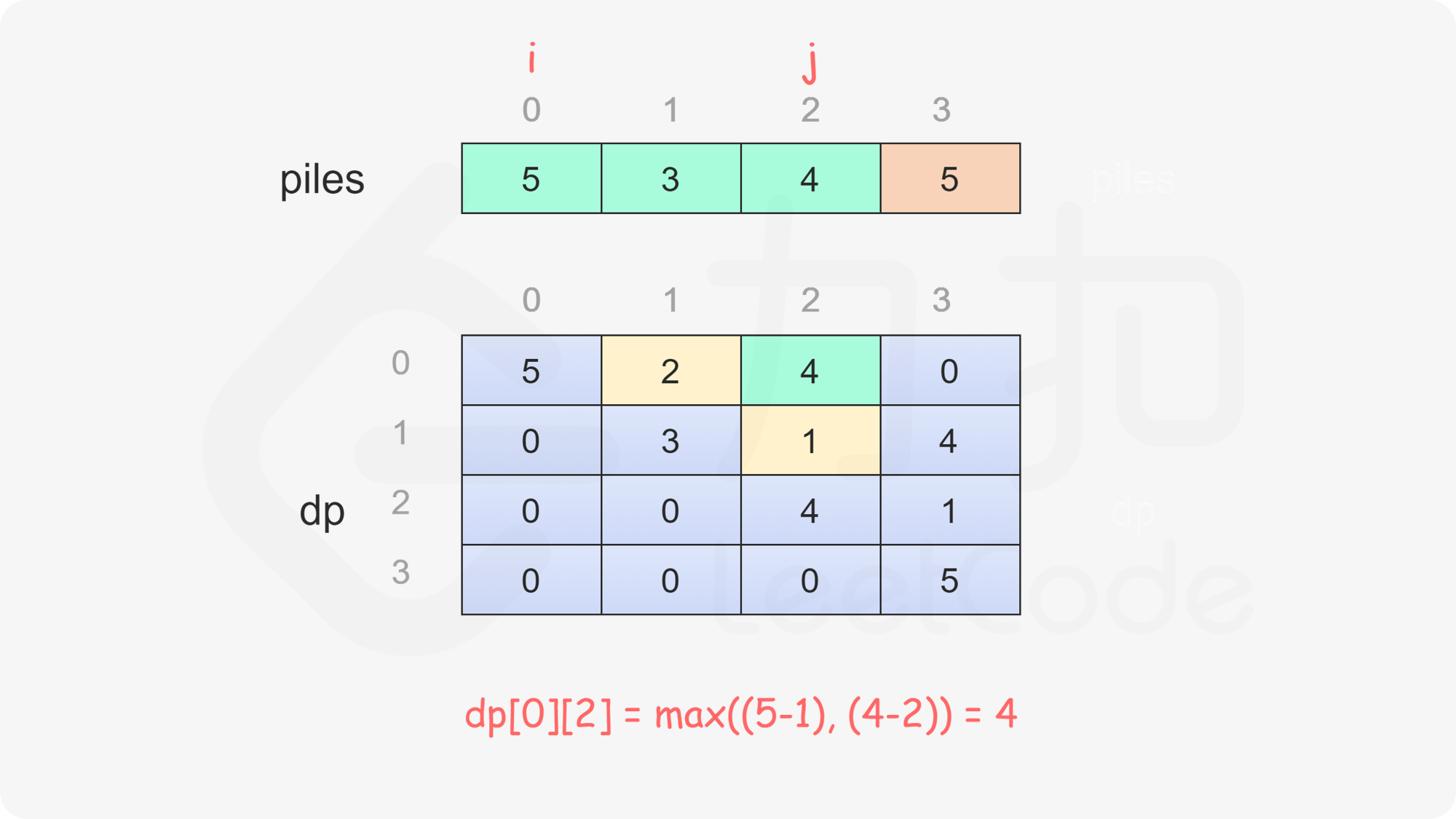
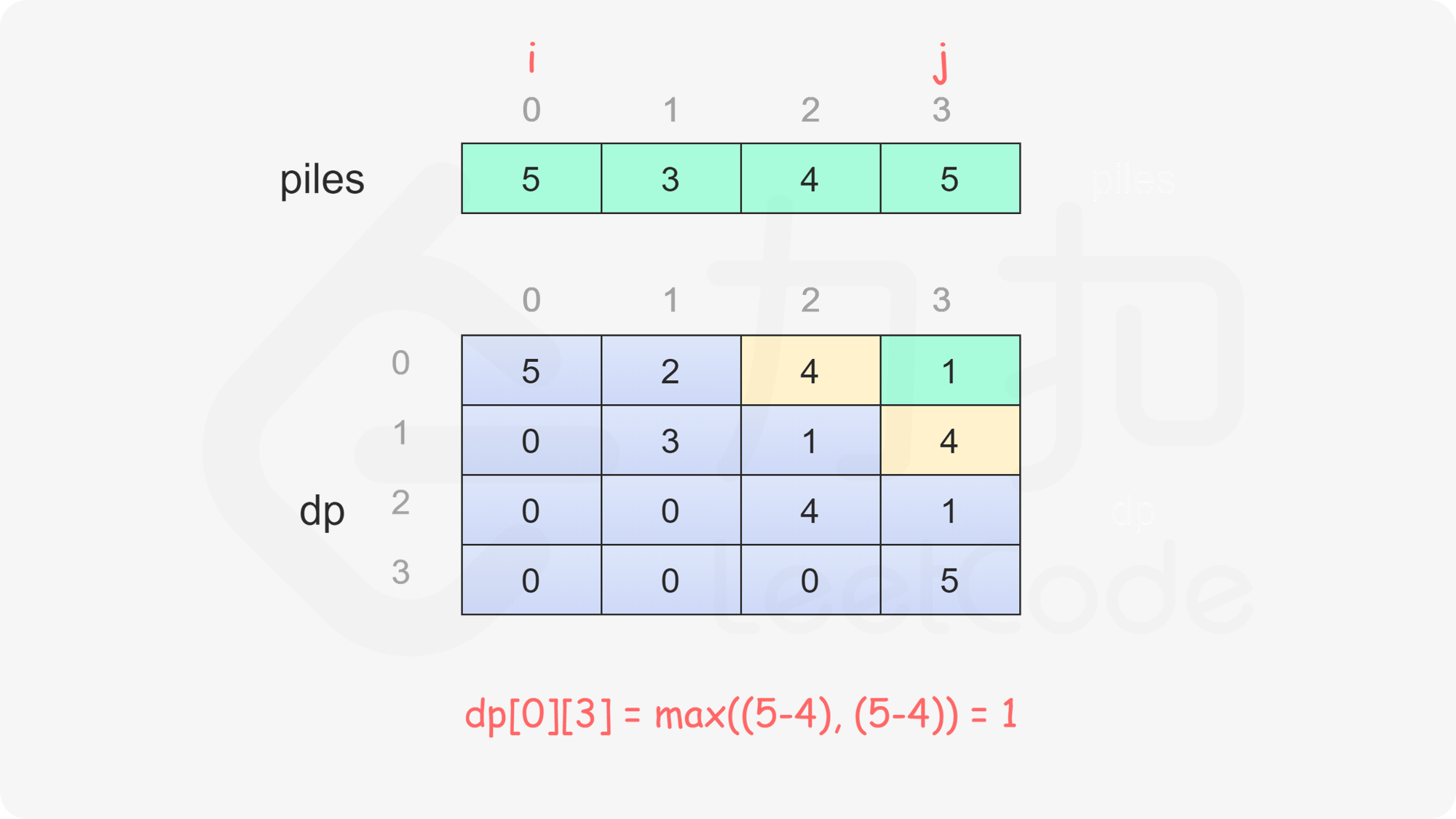
定义二维数组 $\textit{dp}$，其行数和列数都等于石子的堆数，$\textit{dp}[i][j]$ 表示当剩下的石子堆为下标 $i$ 到下标 $j$ 时，即在下标范围 $[i, j]$ 中，当前玩家与另一个玩家的石子数量之差的最大值，注意当前玩家不一定是先手 $\text{Alice}$。

只有当 $i \le j$ 时，剩下的石子堆才有意义，因此当 $i>j$ 时，$\textit{dp}[i][j]=0$。

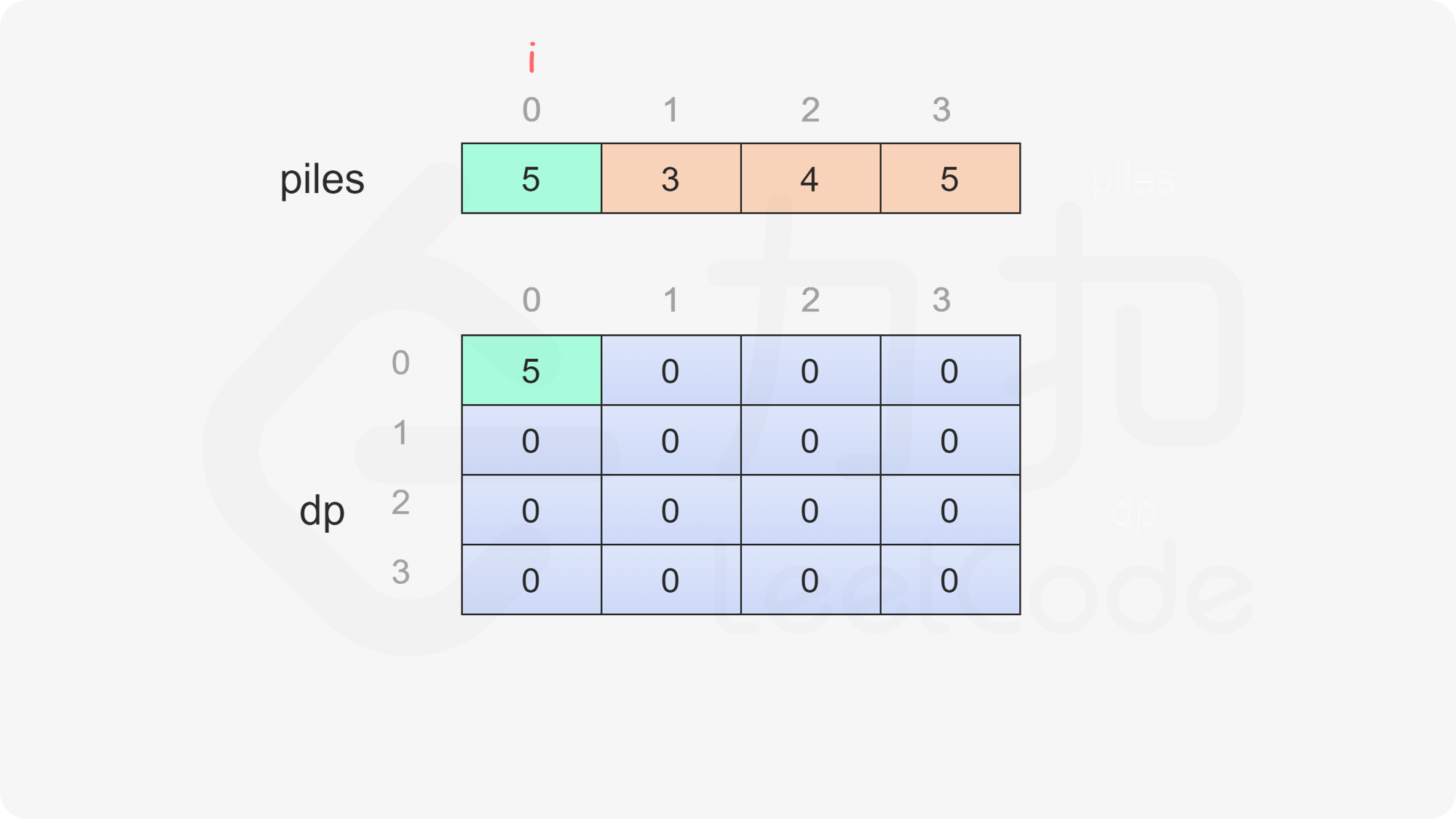
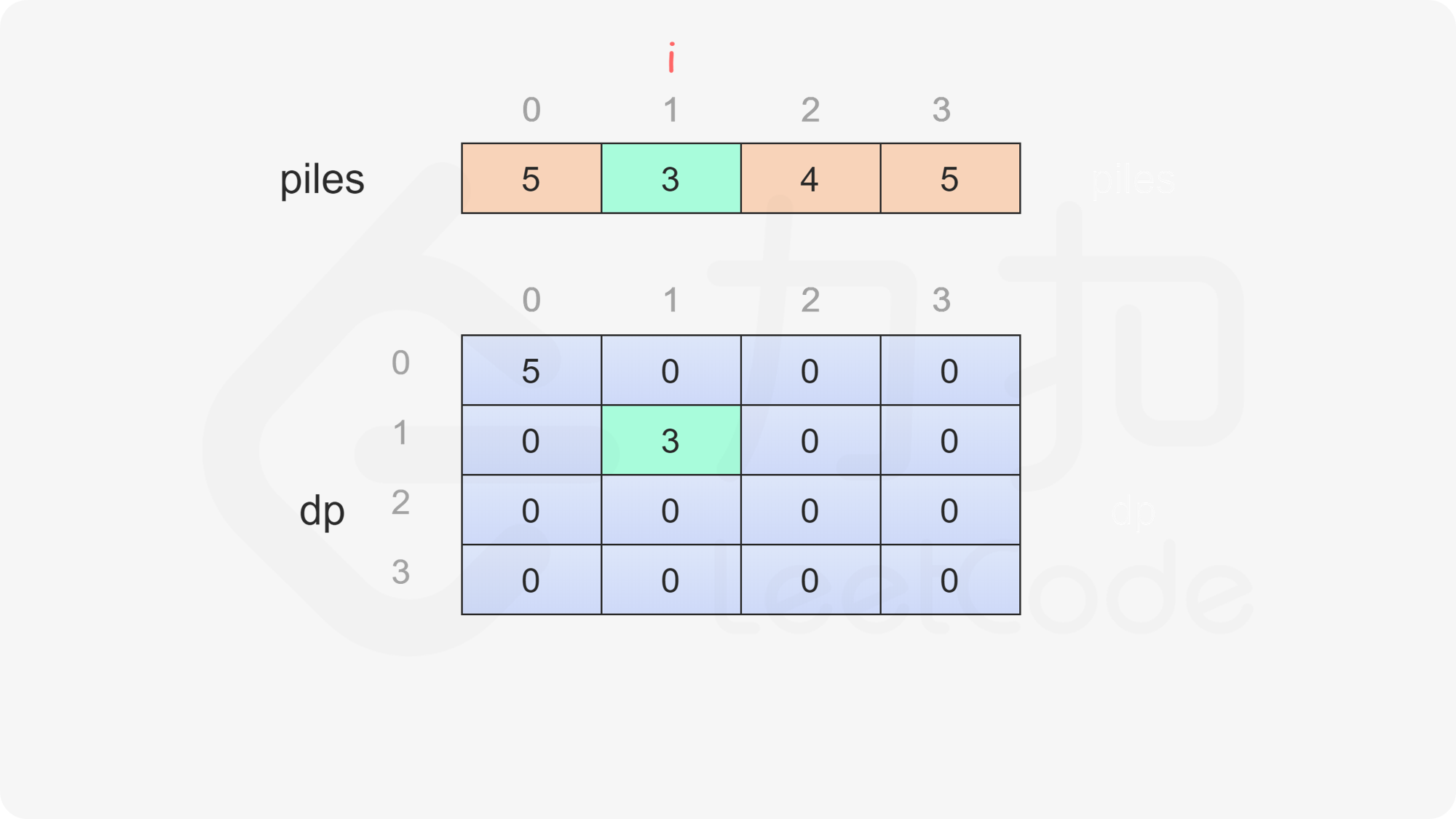
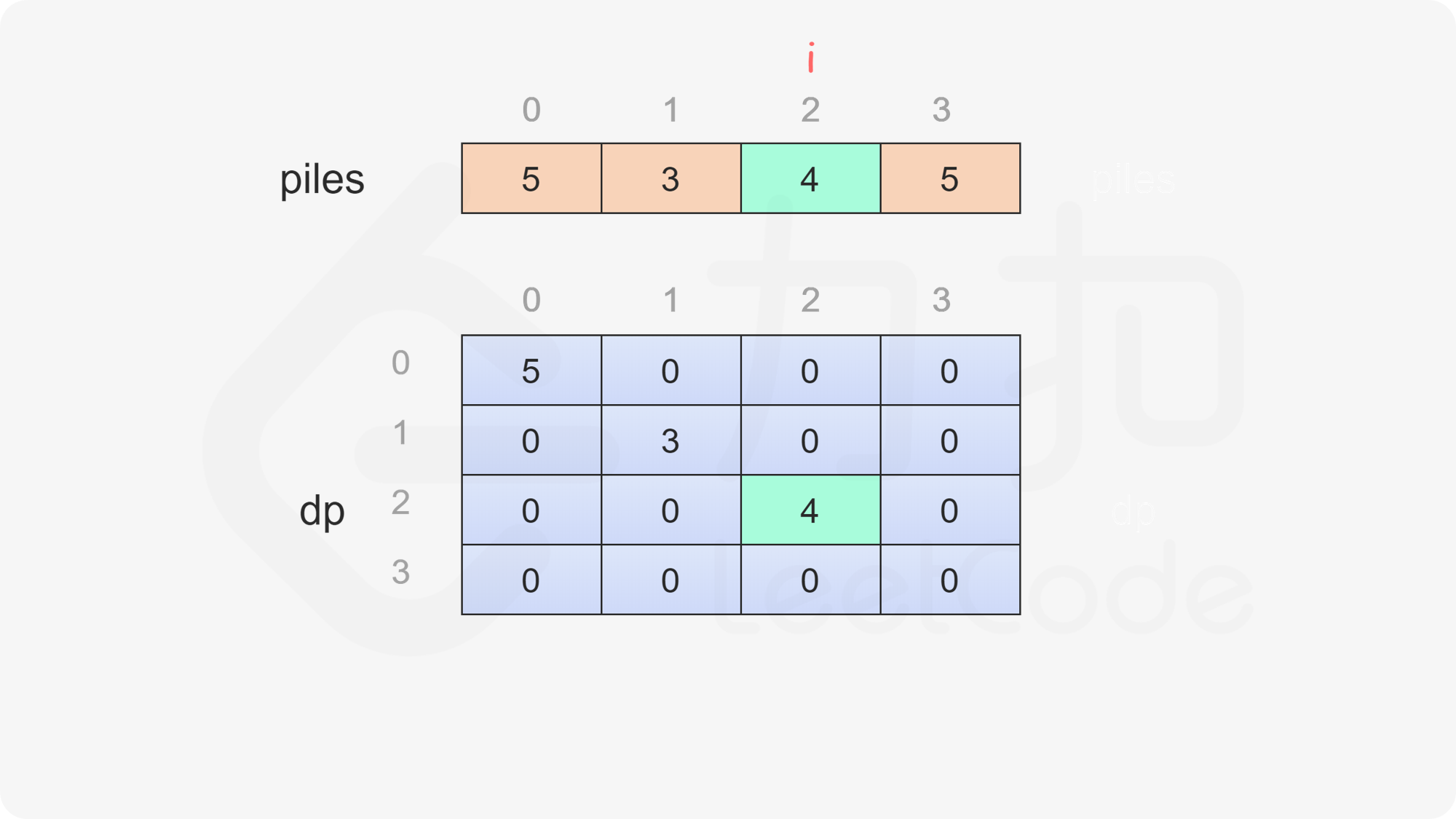
当 $i=j$ 时，只剩下一堆石子，当前玩家只能取走这堆石子，因此对于所有 $0 \le i < \textit{nums}.\text{length}$，都有 $\textit{dp}[i][i]=\textit{piles}[i]$。

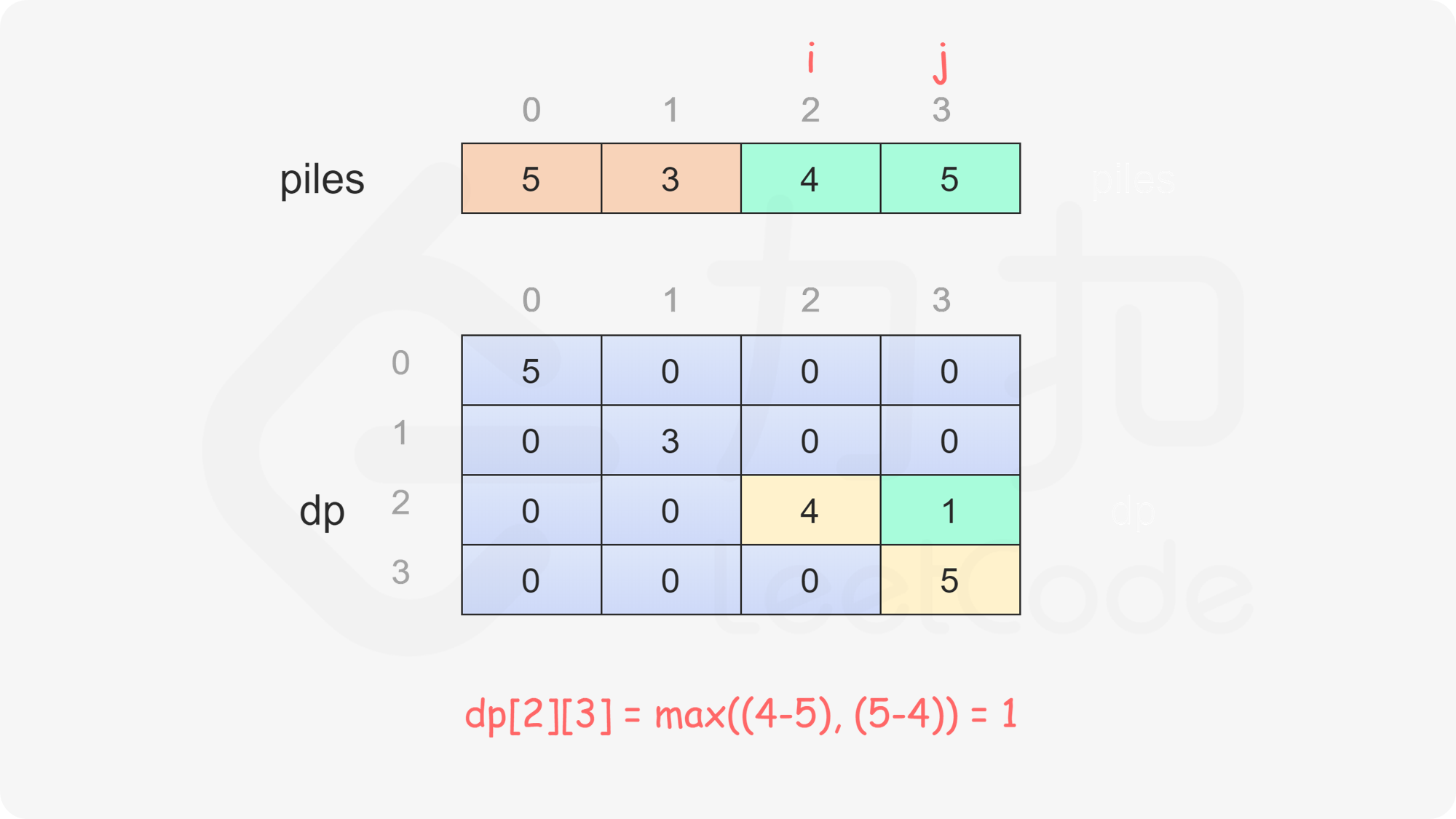
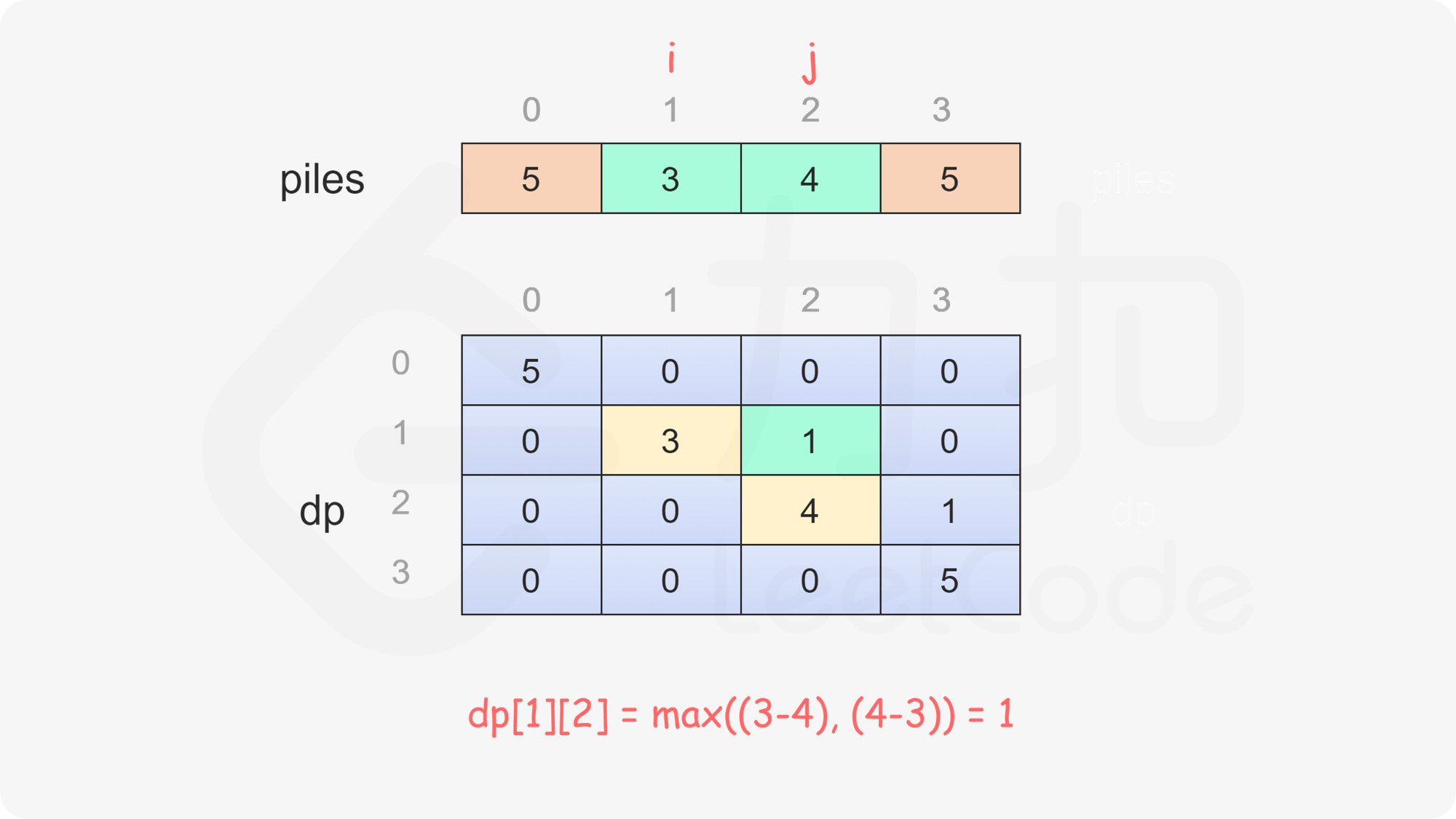
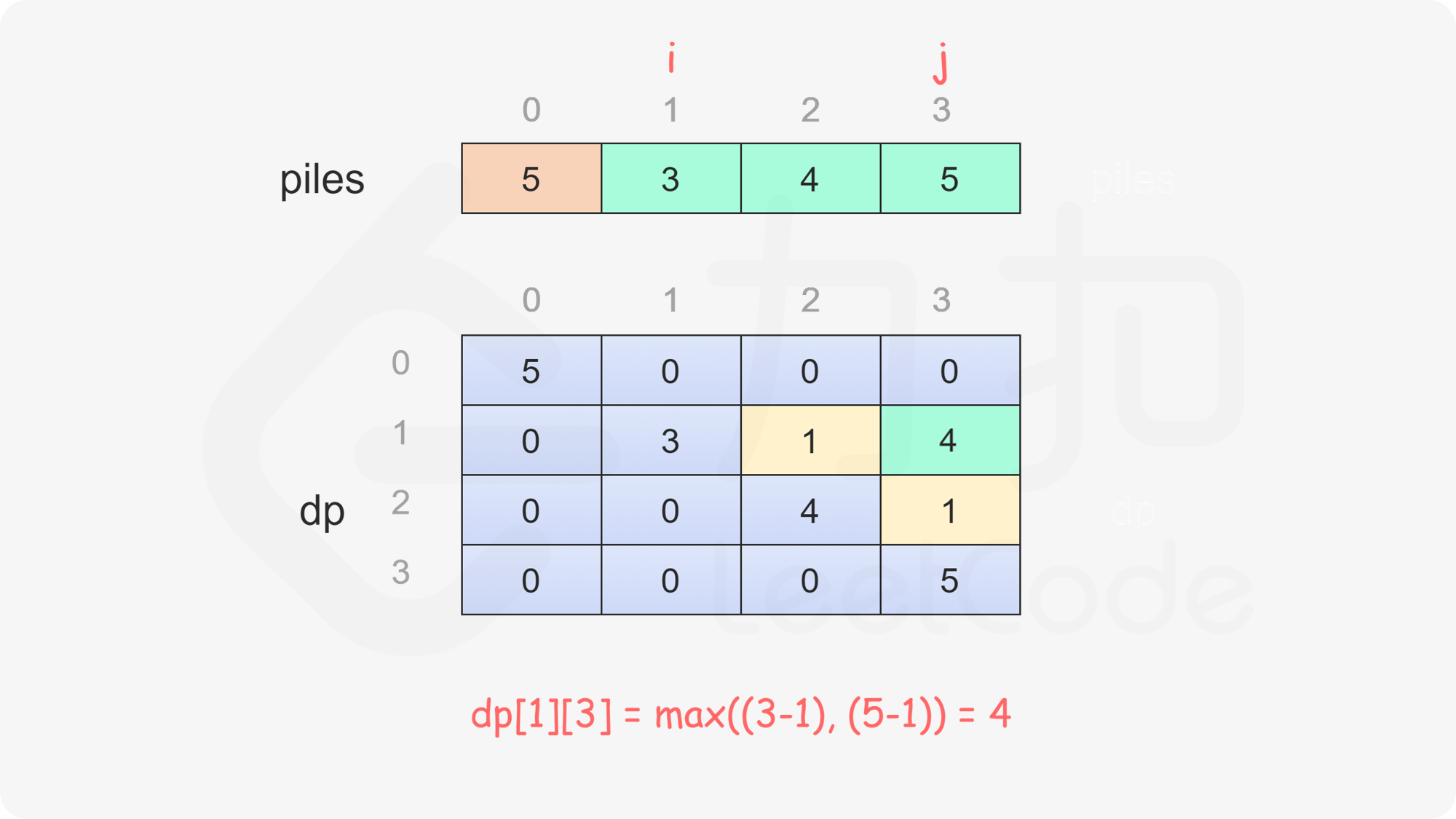
当 $i<j$ 时，当前玩家可以选择取走 $\textit{piles}[i]$ 或 $\textit{piles}[j]$，然后轮到另一个玩家在剩下的石子堆中取走石子。在两种方案中，当前玩家会选择最优的方案，使得自己的石子数量最大化。因此可以得到如下状态转移方程：

$$
\textit{dp}[i][j]=\max(\textit{piles}[i] - \textit{dp}[i+1][j], \textit{piles}[j] - \textit{dp}[i][j-1])
$$

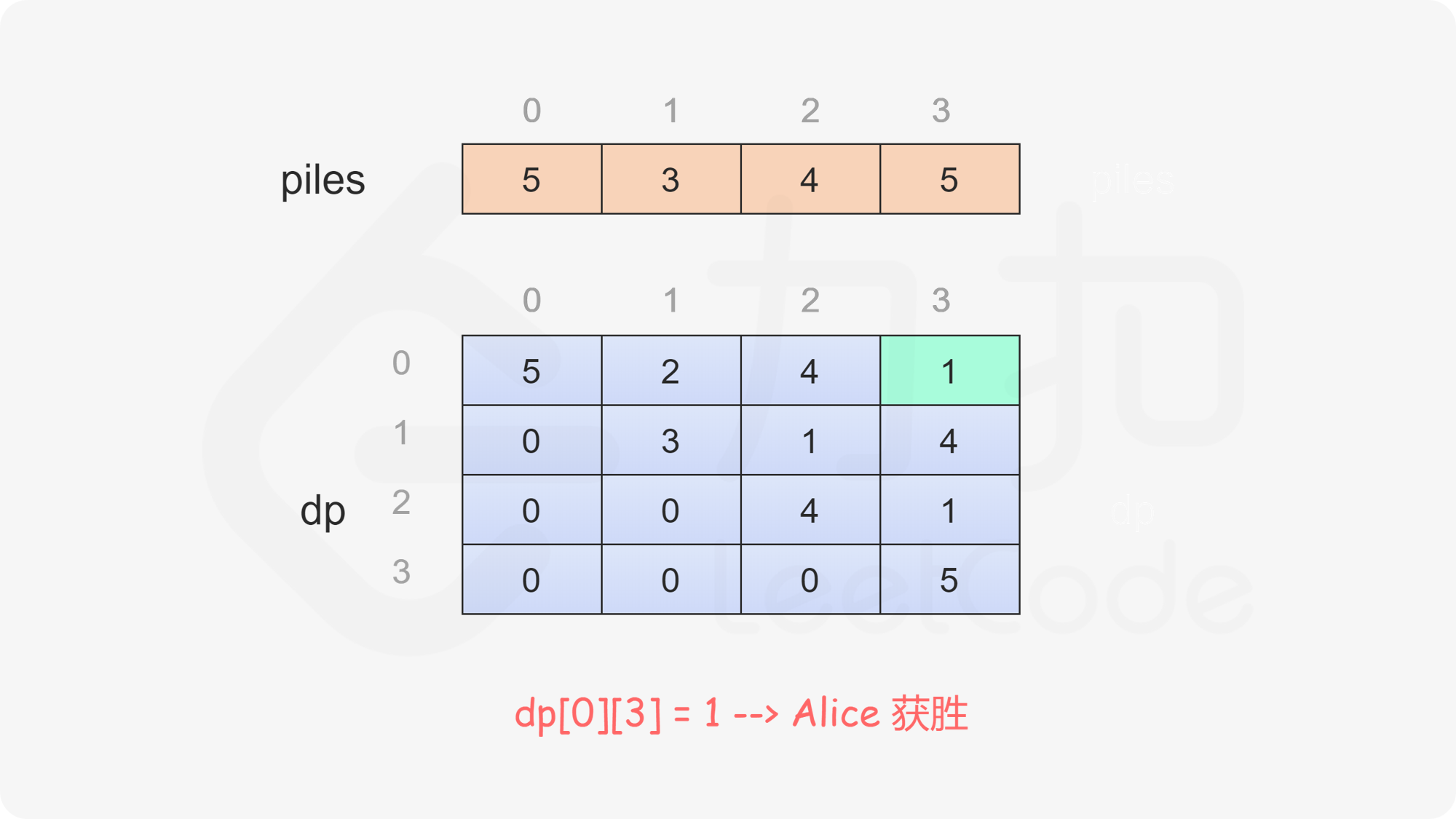
最后判断 $\textit{dp}[0][\textit{piles}.\text{length}-1]$ 的值，如果大于 $0$，则 $\text{Alice}$ 的石子数量大于 $\text{Bob}$ 的石子数量，因此 $\text{Alice}$ 赢得比赛，否则 $\text{Bob}$ 赢得比赛。

<fig1,fig2,fig3,fig4,fig5,fig6,fig7,fig8,fig9,fig10,fig11,fig12>

[sol11-Java]
class Solution {
    public boolean stoneGame(int[] piles) {
        int length = piles.length;
        int[][] dp = new int[length][length];
        for (int i = 0; i < length; i++) {
            dp[i][i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
            }
        }
        return dp[0][length - 1] > 0;
    }
}
[sol11-C#]
public class Solution {
    public bool StoneGame(int[] piles) {
        int length = piles.Length;
        int[,] dp = new int[length, length];
        for (int i = 0; i < length; i++) {
            dp[i, i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[i, j] = Math.Max(piles[i] - dp[i + 1, j], piles[j] - dp[i, j - 1]);
            }
        }
        return dp[0, length - 1] > 0;
    }
}
[sol11-C]
bool stoneGame(int* piles, int pilesSize) {
    int dp[pilesSize][pilesSize];
    for (int i = 0; i < pilesSize; i++) {
        dp[i][i] = piles[i];
    }
    for (int i = pilesSize - 2; i >= 0; i--) {
        for (int j = i + 1; j < pilesSize; j++) {
            dp[i][j] = fmax(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
        }
    }
    return dp[0][pilesSize - 1] > 0;
}
[sol11-C++]
class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int length = piles.size();
        auto dp = vector<vector<int>>(length, vector<int>(length));
        for (int i = 0; i < length; i++) {
            dp[i][i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
            }
        }
        return dp[0][length - 1] > 0;
    }
};
[sol11-Golang]
func stoneGame(piles []int) bool {
    length := len(piles)
    dp := make([][]int, length)
    for i := 0; i < length; i++ {
        dp[i] = make([]int, length)
        dp[i][i] = piles[i]
    }
    for i := length - 2; i >= 0; i-- {
        for j := i + 1; j < length; j++ {
            dp[i][j] = max(piles[i] - dp[i+1][j], piles[j] - dp[i][j-1])
        }
    }
    return dp[0][length-1] > 0
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}
[sol11-Python3]
class Solution:
    def stoneGame(self, piles: List[int]) -> bool:
        length = len(piles)
        dp = [[0] * length for _ in range(length)]
        for i, pile in enumerate(piles):
            dp[i][i] = pile
        for i in range(length - 2, -1, -1):
            for j in range(i + 1, length):
                dp[i][j] = max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1])
        return dp[0][length - 1] > 0
[sol11-JavaScript]
var stoneGame = function(piles) {
    const length = piles.length;
    const dp = new Array(length).fill(0).map(() => new Array(length).fill(0));
    for (let i = 0; i < length; i++) {
        dp[i][i] = piles[i];
    }
    for (let i = length - 2; i >= 0; i--) {
        for (let j = i + 1; j < length; j++) {
            dp[i][j] = Math.max(piles[i] - dp[i + 1][j], piles[j] - dp[i][j - 1]);
        }
    }
    return dp[0][length - 1] > 0;
};

上述代码中使用了二维数组 $\textit{dp}$。分析状态转移方程可以看到，$\textit{dp}[i][j]$ 的值只和 $\textit{dp}[i + 1][j]$ 与 $\textit{dp}[i][j - 1]$ 有关，即在计算 $\textit{dp}$ 的第 $i$ 行的值时，只需要使用到 $\textit{dp}$ 的第 $i$ 行和第 $i+1$ 行的值，因此可以使用一维数组代替二维数组，对空间进行优化。

[sol12-Java]
class Solution {
    public boolean stoneGame(int[] piles) {
        int length = piles.length;
        int[] dp = new int[length];
        for (int i = 0; i < length; i++) {
            dp[i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[j] = Math.max(piles[i] - dp[j], piles[j] - dp[j - 1]);
            }
        }
        return dp[length - 1] > 0;
    }
}
[sol12-C#]
public class Solution {
    public bool StoneGame(int[] piles) {
        int length = piles.Length;
        int[] dp = new int[length];
        for (int i = 0; i < length; i++) {
            dp[i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[j] = Math.Max(piles[i] - dp[j], piles[j] - dp[j - 1]);
            }
        }
        return dp[length - 1] > 0;
    }
}
[sol12-C]
bool stoneGame(int* piles, int pilesSize) {
    int dp[pilesSize];
    for (int i = 0; i < pilesSize; i++) {
        dp[i] = piles[i];
    }
    for (int i = pilesSize - 2; i >= 0; i--) {
        for (int j = i + 1; j < pilesSize; j++) {
            dp[j] = fmax(piles[i] - dp[j], piles[j] - dp[j - 1]);
        }
    }
    return dp[pilesSize - 1] > 0;
}
[sol12-C++]
class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        int length = piles.size();
        auto dp = vector<int>(length);
        for (int i = 0; i < length; i++) {
            dp[i] = piles[i];
        }
        for (int i = length - 2; i >= 0; i--) {
            for (int j = i + 1; j < length; j++) {
                dp[j] = max(piles[i] - dp[j], piles[j] - dp[j - 1]);
            }
        }
        return dp[length - 1] > 0;
    }
};
[sol12-Golang]
func stoneGame(piles []int) bool {
    length := len(piles)
    dp := make([]int, length)
    for i := 0; i < length; i++ {
        dp[i] = piles[i]
    }
    for i := length - 2; i >= 0; i-- {
        for j := i + 1; j < length; j++ {
            dp[j] = max(piles[i] - dp[j], piles[j] - dp[j - 1])
        }
    }
    return dp[length - 1] > 0
}

func max(x, y int) int {
    if x > y {
        return x
    }
    return y
}
[sol12-Python3]
class Solution:
    def stoneGame(self, piles: List[int]) -> bool:
        length = len(piles)
        dp = [0] * length
        for i, pile in enumerate(piles):
            dp[i] = pile
        for i in range(length - 2, -1, -1):
            for j in range(i + 1, length):
                dp[j] = max(piles[i] - dp[j], piles[j] - dp[j - 1])
        return dp[length - 1] > 0
[sol12-JavaScript]
var stoneGame = function(piles) {
    const length = piles.length;
    const dp = new Array(length).fill(0);
    for (let i = 0; i < length; i++) {
        dp[i] = piles[i];
    }
    for (let i = length - 2; i >= 0; i--) {
        for (let j = i + 1; j < length; j++) {
            dp[j] = Math.max(piles[i] - dp[j], piles[j] - dp[j - 1]);
        }
    }
    return dp[length - 1] > 0;
};

复杂度分析

  • 时间复杂度：$O(n^2)$，其中 $n$ 是数组的长度。需要计算每个子数组对应的 $\textit{dp}$ 的值，共有 $\frac{n(n+1)}{2}$ 个子数组。

  • 空间复杂度：$O(n)$，其中 $n$ 是数组的长度。空间复杂度取决于额外创建的数组 $\textit{dp}$，如果不优化空间，则空间复杂度是 $O(n^2)$，使用一维数组优化之后空间复杂度可以降至 $O(n)$。

方法二：数学

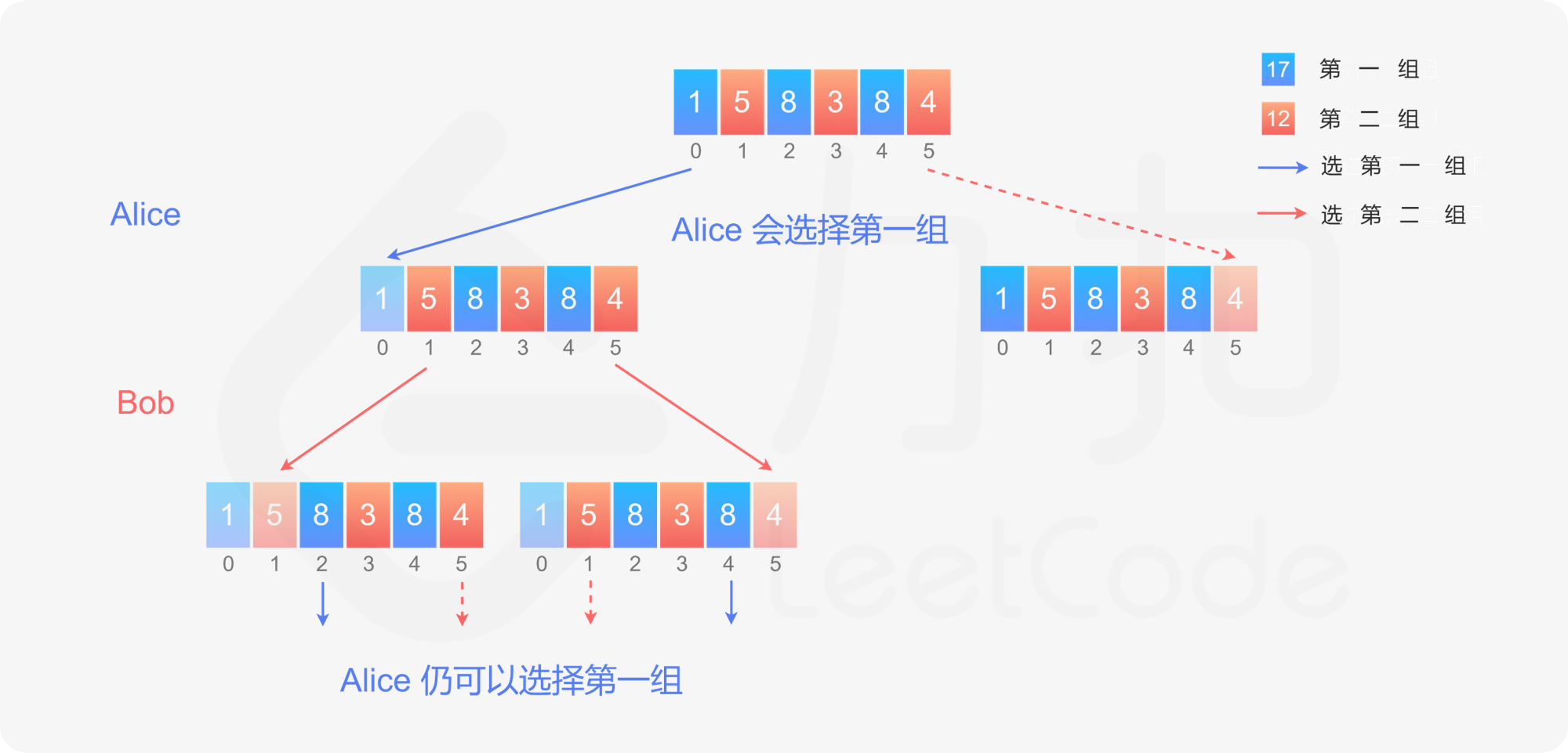
假设有 $n$ 堆石子，$n$ 是偶数，则每堆石子的下标从 $0$ 到 $n-1$。根据下标将 $n$ 堆石子分成两组，每组有 $\frac{n}{2}$ 堆石子，下标为偶数的石子堆属于第一组，下标为奇数的石子堆属于第二组。

初始时，行的开始处的石子堆位于下标 $0$，属于第一组，行的结束处的石子堆位于下标 $n-1$，属于第二组，因此作为先手的 $\text{Alice}$ 可以自由选择取走第一组的一堆石子或者第二组的一堆石子。如果 $\text{Alice}$ 取走第一组的一堆石子，则剩下的部分在行的开始处和结束处的石子堆都属于第二组，因此 $\text{Bob}$ 只能取走第二组的一堆石子。如果 $\text{Alice}$ 取走第二组的一堆石子，则剩下的部分在行的开始处和结束处的石子堆都属于第一组，因此 $\text{Bob}$ 只能取走第一组的一堆石子。无论 $\text{Bob}$ 取走的是开始处还是结束处的一堆石子，剩下的部分在行的开始处和结束处的石子堆一定是属于不同组的，因此轮到 $\text{Alice}$ 取走石子时，$\text{Alice}$ 又可以在两组石子之间进行自由选择。

根据上述分析可知，作为先手的 $\text{Alice}$ 可以在第一次取走石子时就决定取走哪一组的石子，并全程取走同一组的石子。既然如此，$\text{Alice}$ 是否有必胜策略？

答案是肯定的。将石子分成两组之后，可以计算出每一组的石子数量，同时知道哪一组的石子数量更多。$\text{Alice}$ 只要选择取走数量更多的一组石子即可。因此，$\text{Alice}$ 总是可以赢得比赛。

fig1

[sol2-Java]
class Solution {
    public boolean stoneGame(int[] piles) {
        return true;
    }
}
[sol2-C#]
public class Solution {
    public bool StoneGame(int[] piles) {
        return true;
    }
}
[sol2-C]
bool stoneGame(int* piles, int pilesSize) {
    return true;
}
[sol2-C++]
class Solution {
public:
    bool stoneGame(vector<int>& piles) {
        return true;
    }
};
[sol2-Golang]
func stoneGame(piles []int) bool {
    return true
}
[sol2-Python3]
class Solution:
    def stoneGame(self, piles: List[int]) -> bool:
        return True
[sol2-JavaScript]
var stoneGame = function(piles) {
    return true;
};

复杂度分析

  • 时间复杂度：$O(1)$。

  • 空间复杂度：$O(1)$。

统计信息

通过次数 提交次数 AC比率
70271 92782 75.7%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
动态规划 数组 数学 博弈
上一篇:
876-链表的中间结点(Middle of the Linked List)
下一篇:
878-第 N 个神奇数字(Nth Magical Number)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo