原文链接: https://leetcode-cn.com/problems/all-possible-full-binary-trees

英文原文

Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

 

Example 1:

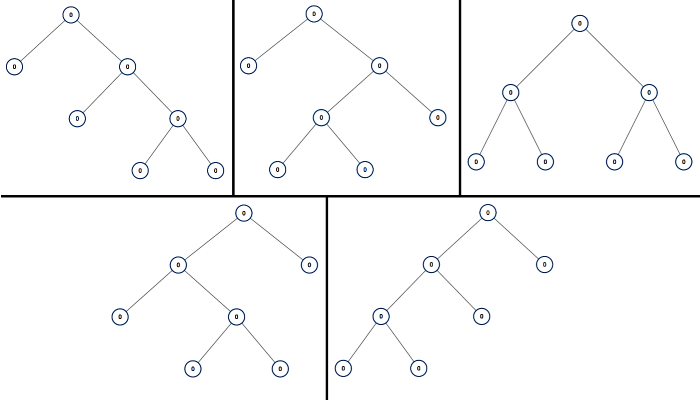
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Example 2:

Input: n = 3
Output: [[0,0,0]]

 

Constraints:

• 1 <= n <= 20

中文题目

满二叉树是一类二叉树，其中每个结点恰好有 0 或 2 个子结点。

返回包含 N 个结点的所有可能满二叉树的列表。 答案的每个元素都是一个可能树的根结点。

答案中每个树的每个结点都必须有 node.val=0。

你可以按任何顺序返回树的最终列表。

 

示例：

输入：7
输出：[[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
解释：

 

提示：

• 1 <= N <= 20

通过代码

官方题解

方法：递归

思路与算法

令 $\text{FBT}(N)$ 作为所有含 $N$ 个结点的可能的满二叉树的列表。

每个满二叉树 $T$ 含有 3 个或更多结点，在其根结点处有 2 个子结点。这些子结点 left 和 right 本身就是满二叉树。

因此，对于 $N \geq 3$，我们可以设定如下的递归策略：$\text{FBT}(N) =$ [对于所有的 $x$，所有的树的左子结点来自 $\text{FBT}(x)$ 而右子结点来自 $\text{FBT}(N-1-x)$]。

此外，通过简单的计数参数，没有满二叉树具有正偶数个结点。

最后，我们应该缓存函数 $\text{FBT}$ 之前的结果，这样我们就不必在递归中重新计算它们。

[SVf3cp4a-Java]
class Solution {
    Map<Integer, List<TreeNode>> memo = new HashMap();

    public List<TreeNode> allPossibleFBT(int N) {
        if (!memo.containsKey(N)) {
            List<TreeNode> ans = new LinkedList();
            if (N == 1) {
                ans.add(new TreeNode(0));
            } else if (N % 2 == 1) {
                for (int x = 0; x < N; ++x) {
                    int y = N - 1 - x;
                    for (TreeNode left: allPossibleFBT(x))
                        for (TreeNode right: allPossibleFBT(y)) {
                            TreeNode bns = new TreeNode(0);
                            bns.left = left;
                            bns.right = right;
                            ans.add(bns);
                        }
                }
            }
            memo.put(N, ans);
        }

        return memo.get(N);
    }
}

[SVf3cp4a-Python]
class Solution(object):
    memo = {0: [], 1: [TreeNode(0)]}

    def allPossibleFBT(self, N):
        if N not in Solution.memo:
            ans = []
            for x in xrange(N):
                y = N - 1 - x
                for left in self.allPossibleFBT(x):
                    for right in self.allPossibleFBT(y):
                        bns = TreeNode(0)
                        bns.left = left
                        bns.right = right
                        ans.append(bns)
            Solution.memo[N] = ans

        return Solution.memo[N]

复杂度分析

• 时间复杂度：$O(2^N)$，对于 $N$ 是奇数的情况，令 $N = 2k + 1$。然后，$\Big| \text{FBT}(N) \Big| = C_k$，第 $k$ 个卡特兰数（Catalan Number）；以及 $\sum\limits_{k < \frac{N}{2}} C_k$（计算中间结果所涉及的复杂度） 限制在 $O(2^N)$内。但是，证明超出了本文的范围。

• 空间复杂度：$O(2^N)$。

统计信息

通过次数	提交次数	AC比率
13747	17730	77.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言