原文链接: https://leetcode-cn.com/problems/complete-binary-tree-inserter

英文原文

A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.

Design an algorithm to insert a new node to a complete binary tree keeping it complete after the insertion.

Implement the CBTInserter class:

• CBTInserter(TreeNode root) Initializes the data structure with the root of the complete binary tree.
• int insert(int v) Inserts a TreeNode into the tree with value Node.val == val so that the tree remains complete, and returns the value of the parent of the inserted TreeNode.
• TreeNode get_root() Returns the root node of the tree.

 

Example 1:

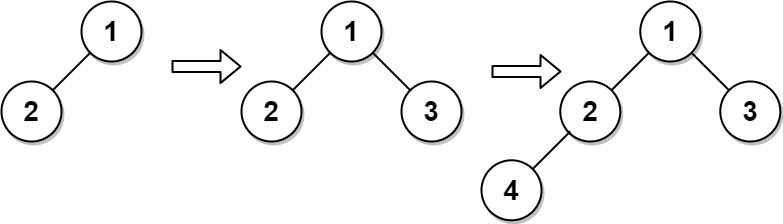
Input
["CBTInserter", "insert", "insert", "get_root"]
[[[1, 2]], [3], [4], []]
Output
[null, 1, 2, [1, 2, 3, 4]]

Explanation
CBTInserter cBTInserter = new CBTInserter([1, 2]);
cBTInserter.insert(3);  // return 1
cBTInserter.insert(4);  // return 2
cBTInserter.get_root(); // return [1, 2, 3, 4]

 

Constraints:

• The number of nodes in the tree will be in the range [1, 1000].
• 0 <= Node.val <= 5000
• root is a complete binary tree.
• 0 <= val <= 5000
• At most 104 calls will be made to insert and get_root.

中文题目

完全二叉树是每一层（除最后一层外）都是完全填充（即，节点数达到最大）的，并且所有的节点都尽可能地集中在左侧。

设计一个用完全二叉树初始化的数据结构 CBTInserter，它支持以下几种操作：

• CBTInserter(TreeNode root) 使用头节点为 root 的给定树初始化该数据结构；
• CBTInserter.insert(int v)  向树中插入一个新节点，节点类型为 TreeNode，值为 v 。使树保持完全二叉树的状态，并返回插入的新节点的父节点的值；
• CBTInserter.get_root() 将返回树的头节点。

 

示例 1：

输入：inputs = ["CBTInserter","insert","get_root"], inputs = [[[1]],[2],[]]
输出：[null,1,[1,2]]

示例 2：

输入：inputs = ["CBTInserter","insert","insert","get_root"], inputs = [[[1,2,3,4,5,6]],[7],[8],[]]
输出：[null,3,4,[1,2,3,4,5,6,7,8]]

 

提示：

1. 最初给定的树是完全二叉树，且包含 1 到 1000 个节点。
2. 每个测试用例最多调用 CBTInserter.insert  操作 10000 次。
3. 给定节点或插入节点的每个值都在 0 到 5000 之间。

通过代码

官方题解

方法 1：双端队列

想法

将所有节点编号，按照从上到下从左到右的顺序。

在每个插入步骤中，我们希望插入到一个编号最小的节点（这样有 0 或者 1 个孩子）。

通过维护一个 deque （双端队列），保存这些节点的编号，我们可以解决这个问题。插入一个节点之后，将成为最高编号的节点，并且没有孩子，所以插入到队列的后端。为了找到最小数字的节点，我们从队列前端弹出元素。

算法

首先，通过广度优先搜索将 deque 中插入含有 0 个或者 1 个孩子的节点编号。

然后插入节点，父亲是 deque 的第一个元素，我们将新节点加入我们的 deque。

[]
class CBTInserter {
    TreeNode root;
    Deque<TreeNode> deque;
    public CBTInserter(TreeNode root) {
        this.root = root;
        deque = new LinkedList();
        Queue<TreeNode> queue = new LinkedList();
        queue.offer(root);

        // BFS to populate deque
        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            if (node.left == null || node.right == null)
                deque.offerLast(node);
            if (node.left != null)
                queue.offer(node.left);
            if (node.right != null)
                queue.offer(node.right);
        }
    }

    public int insert(int v) {
        TreeNode node = deque.peekFirst();
        deque.offerLast(new TreeNode(v));
        if (node.left == null)
            node.left = deque.peekLast();
        else {
            node.right = deque.peekLast();
            deque.pollFirst();
        }

        return node.val;
    }

    public TreeNode get_root() {
        return root;
    }
}

[]
class CBTInserter(object):
    def __init__(self, root):
        self.deque = collections.deque()
        self.root = root
        q = collections.deque([root])
        while q:
            node = q.popleft()
            if not node.left or not node.right:
                self.deque.append(node)
            if node.left:
                q.append(node.left)
            if node.right:
                q.append(node.right)

    def insert(self, v):
        node = self.deque[0]
        self.deque.append(TreeNode(v))
        if not node.left:
            node.left = self.deque[-1]
        else:
            node.right = self.deque[-1]
            self.deque.popleft()
        return node.val

    def get_root(self):
        return self.root

复杂度分析

• 时间复杂度：预处理 $O(N)$，其中 $N$ 是树上节点编号。每个插入步骤是 $O(1)$。
• 空间复杂度：$O(N_\text{cur})$，其中当前插入操作树的大小为 $N_{\text{cur}}$。

统计信息

通过次数	提交次数	AC比率
5907	9185	64.3%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言