原文链接: https://leetcode-cn.com/problems/minimum-falling-path-sum

英文原文

Given an n x n array of integers matrix, return the minimum sum of any falling path through matrix.

A falling path starts at any element in the first row and chooses the element in the next row that is either directly below or diagonally left/right. Specifically, the next element from position (row, col) will be (row + 1, col - 1), (row + 1, col), or (row + 1, col + 1).

 

Example 1:

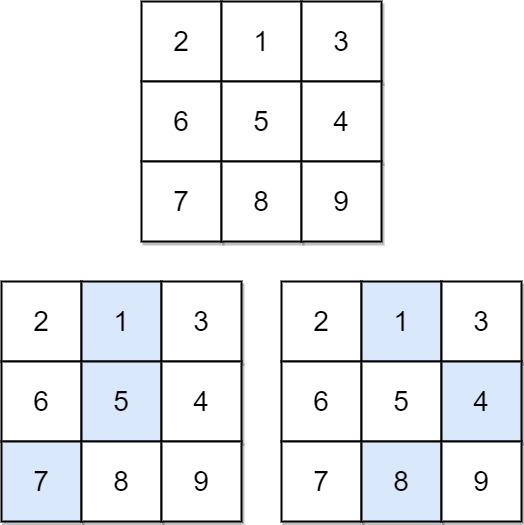
Input: matrix = [[2,1,3],[6,5,4],[7,8,9]]
Output: 13
Explanation: There are two falling paths with a minimum sum as shown.

Example 2:

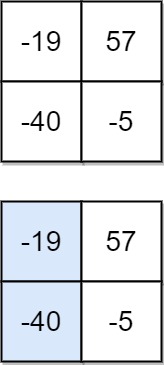
Input: matrix = [[-19,57],[-40,-5]]
Output: -59
Explanation: The falling path with a minimum sum is shown.

 

Constraints:

• n == matrix.length == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

中文题目

给你一个 n x n 的 方形 整数数组 matrix ，请你找出并返回通过 matrix 的下降路径 的 最小和 。

下降路径 可以从第一行中的任何元素开始，并从每一行中选择一个元素。在下一行选择的元素和当前行所选元素最多相隔一列（即位于正下方或者沿对角线向左或者向右的第一个元素）。具体来说，位置 (row, col) 的下一个元素应当是 (row + 1, col - 1)、(row + 1, col) 或者 (row + 1, col + 1) 。

 

示例 1：

输入：matrix = [[2,1,3],[6,5,4],[7,8,9]]
输出：13
解释：下面是两条和最小的下降路径，用加粗+斜体标注：
[[2,1,3],      [[2,1,3],
 [6,5,4],       [6,5,4],
 [7,8,9]]       [7,8,9]]

示例 2：

输入：matrix = [[-19,57],[-40,-5]]
输出：-59
解释：下面是一条和最小的下降路径，用加粗+斜体标注：
[[-19,57],
 [-40,-5]]

示例 3：

输入：matrix = [[-48]]
输出：-48

 

提示：

• n == matrix.length
• n == matrix[i].length
• 1 <= n <= 100
• -100 <= matrix[i][j] <= 100

通过代码

官方题解

方法一：动态规划

分析

我们用 dp(r, c) 表示从位置为 (r, c) 的元素开始的下降路径最小和。根据题目的要求，位置 (r, c) 可以下降到 (r + 1, c - 1)，(r + 1, c) 和 (r + 1, c + 1) 三个位置（先不考虑超出数组边界的情况），因此状态转移方程为：

dp(r, c) = A[r][c] + min{dp(r + 1, c - 1), dp(r + 1, c), dp(r + 1, c + 1)}

由于下降路径可以从第一行中的任何元素开始，因此最终的答案为 $\min\limits_c \mathrm{dp}(0, c)$。

算法

我们可以直接在原数组 A 上计算 dp(r, c)，因为最后一行 A 的值就是 dp 的值 。因此我们从倒数第二行开始，从下往上进行动态规划，状态转移方程为：

A[r][c] = A[r][c] + min{A[r + 1][c - 1], A[r + 1][c], A[r + 1][c + 1]}

注意需要处理超出边界的情况，即在第一列和最后一列只能下降到两个位置。

我们用一个例子来解释动态规划的正确性。假设数组 A 为 [[1,1,1],[5,3,1],[2,3,4]]，我们现在在位置 (1, 0) 有 A[1][0] = 5，可以选择下降到位置 (2, 0) 选择元素 2，或者下降到位置 (2, 1) 选择元素 3。由于 2 比 3 小，因此我们选择下降到位置 (2, 0)，有dp(1, 0) = 5 + 2 = 7。

在依次处理完位置 (1, 0)，(1, 1) 和 (1, 2) 后，数组 A 变成了 [[1,1,1],[7,5,4],[2,3,4]]。我们继续向上处理位置 (0, 0)，(0, 1) 和 (0, 2)，最终数组 A 为 [[6,5,5],[7,5,4],[2,3,4]]，因此最终的答案为 min(A[0]) = 5。

[sol1]
class Solution {
    public int minFallingPathSum(int[][] A) {
        int N = A.length;
        for (int r = N-2; r >= 0; --r) {
            for (int c = 0; c < N; ++c) {
                // best = min(A[r+1][c-1], A[r+1][c], A[r+1][c+1])
                int best = A[r+1][c];
                if (c > 0)
                    best = Math.min(best, A[r+1][c-1]);
                if (c+1 < N)
                    best = Math.min(best, A[r+1][c+1]);
                A[r][c] += best;
            }
        }

        int ans = Integer.MAX_VALUE;
        for (int x: A[0])
            ans = Math.min(ans, x);
        return ans;
    }
}

[sol1]
class Solution(object):
    def minFallingPathSum(self, A):
        while len(A) >= 2:
            row = A.pop()            
            for i in xrange(len(row)):
                A[-1][i] += min(row[max(0,i-1): min(len(row), i+2)])
        return min(A[0])

复杂度分析

• 时间复杂度：$O(N^2)$，其中 $N$ 是数组 A 的边长。

• 空间复杂度：$O(N^2)$。如果考虑的是额外空间复杂度，那么在使用数组 A 直接计算 dp 值时，额外空间复杂度为 $O(1)$。

统计信息

通过次数	提交次数	AC比率
24545	36629	67.0%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言