英文原文
The chess knight has a unique movement, it may move two squares vertically and one square horizontally, or two squares horizontally and one square vertically (with both forming the shape of an L). The possible movements of chess knight are shown in this diagaram:
A chess knight can move as indicated in the chess diagram below:
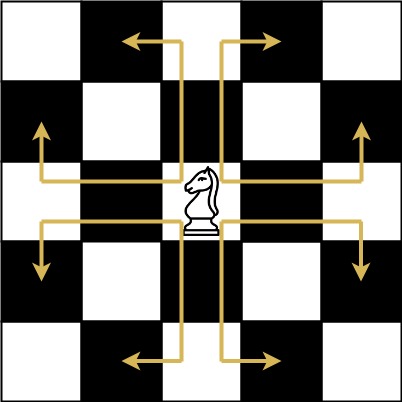
We have a chess knight and a phone pad as shown below, the knight can only stand on a numeric cell (i.e. blue cell).
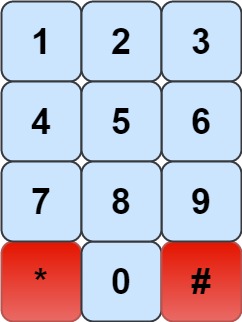
Given an integer n, return how many distinct phone numbers of length n we can dial.
You are allowed to place the knight on any numeric cell initially and then you should perform n - 1 jumps to dial a number of length n. All jumps should be valid knight jumps.
As the answer may be very large, return the answer modulo 109 + 7.
Example 1:
Input: n = 1 Output: 10 Explanation: We need to dial a number of length 1, so placing the knight over any numeric cell of the 10 cells is sufficient.
Example 2:
Input: n = 2 Output: 20 Explanation: All the valid number we can dial are [04, 06, 16, 18, 27, 29, 34, 38, 40, 43, 49, 60, 61, 67, 72, 76, 81, 83, 92, 94]
Example 3:
Input: n = 3 Output: 46
Example 4:
Input: n = 4 Output: 104
Example 5:
Input: n = 3131 Output: 136006598 Explanation: Please take care of the mod.
Constraints:
1 <= n <= 5000
中文题目
国际象棋中的骑士可以按下图所示进行移动:
 .
. 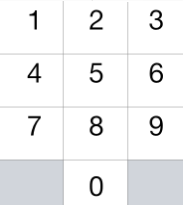
这一次,我们将 “骑士” 放在电话拨号盘的任意数字键(如上图所示)上,接下来,骑士将会跳 N-1 步。每一步必须是从一个数字键跳到另一个数字键。
每当它落在一个键上(包括骑士的初始位置),都会拨出键所对应的数字,总共按下 N 位数字。
你能用这种方式拨出多少个不同的号码?
因为答案可能很大,所以输出答案模 10^9 + 7。
示例 1:
输入:1 输出:10
示例 2:
输入:2 输出:20
示例 3:
输入:3 输出:46
提示:
1 <= N <= 5000
通过代码
官方题解
方法一:动态规划
我们用 f(start, n) 表示骑士从数字 start 开始,跳了 n - 1 步得到不同的 n 位数字的个数。f(start, n) 可以从 f(x, n - 1) 转移而来,其中 x 是任意一个可以一步跳到 start 的数字。例如当 start = 1,时,x 可以为 6 或 8,因此有 f(1, n) = f(6, n - 1) + f(8, n - 1)。
最终的答案即为 f(0, N) + f(1, N) + ... + f(9, N)。我们可以使用滚动数组减少空间复杂度,这是因为 f(start, n) 只和 f(x, n - 1) 有关,因此在计算 f(start, n) 时,所有第二维小于 n - 1 的 f 值都不必存储。也就是说,我们只要实时存储当前正在计算的所有 f 值(n 位数字)以及上一个状态的 f 值(n - 1 位数字)即可。在 Java 代码中,我们使用 dp[0][start] 和 dp[1][start] 交替表示当前和上一个状态的 f 值。在 Python 代码中,我们使用 dp2 数组计算出当前的 f 值后,直接覆盖存储了上一个状态的 f 值的 dp 数组。
[sol1]class Solution { public int knightDialer(int N) { int MOD = 1_000_000_007; int[][] moves = new int[][]{ {4,6},{6,8},{7,9},{4,8},{3,9,0}, {},{1,7,0},{2,6},{1,3},{2,4}}; int[][] dp = new int[2][10]; Arrays.fill(dp[0], 1); for (int hops = 0; hops < N-1; ++hops) { Arrays.fill(dp[~hops & 1], 0); for (int node = 0; node < 10; ++node) for (int nei: moves[node]) { dp[~hops & 1][nei] += dp[hops & 1][node]; dp[~hops & 1][nei] %= MOD; } } long ans = 0; for (int x: dp[~N & 1]) ans += x; return (int) (ans % MOD); } }
[sol1]class Solution(object): def knightDialer(self, N): MOD = 10**9 + 7 moves = [[4,6],[6,8],[7,9],[4,8],[3,9,0],[], [1,7,0],[2,6],[1,3],[2,4]] dp = [1] * 10 for hops in xrange(N-1): dp2 = [0] * 10 for node, count in enumerate(dp): for nei in moves[node]: dp2[nei] += count dp2[nei] %= MOD dp = dp2 return sum(dp) % MOD
复杂度分析
时间复杂度:$O(N)$。
空间复杂度:如果使用滚动数组,则空间复杂度为 $O(1)$,也可以看成 $O(10)$。否则空间复杂度为 $O(N)$。
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 6418 | 13416 | 47.8% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|




