原文链接: https://leetcode-cn.com/problems/regions-cut-by-slashes
英文原文
An n x n grid is composed of 1 x 1 squares where each 1 x 1 square consists of a '/', '\', or blank space ' '. These characters divide the square into contiguous regions.
Given the grid grid represented as a string array, return the number of regions.
Note that backslash characters are escaped, so a '\' is represented as '\\'.
Example 1:

Input: grid = [" /","/ "] Output: 2
Example 2:

Input: grid = [" /"," "] Output: 1
Example 3:

Input: grid = ["\\/","/\\"] Output: 4 Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
Example 4:

Input: grid = ["/\\","\\/"] Output: 5 Explanation: (Recall that because \ characters are escaped, "\\/" refers to \/, and "/\\" refers to /\.)
Example 5:

Input: grid = ["//","/ "] Output: 3
Constraints:
n == grid.lengthn == grid[i].length1 <= n <= 30grid[i][j]is either'/','\', or' '.
中文题目
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 "\\" 表示。)。
返回区域的数目。
示例 1:
输入: [ " /", "/ " ] 输出:2 解释:2x2 网格如下:
示例 2:
输入: [ " /", " " ] 输出:1 解释:2x2 网格如下:
示例 3:
输入: [ "\\/", "/\\" ] 输出:4 解释:(回想一下,因为 \ 字符是转义的,所以 "\\/" 表示 \/,而 "/\\" 表示 /\。) 2x2 网格如下:
示例 4:
输入: [ "/\\", "\\/" ] 输出:5 解释:(回想一下,因为 \ 字符是转义的,所以 "/\\" 表示 /\,而 "\\/" 表示 \/。) 2x2 网格如下:
示例 5:
输入: [ "//", "/ " ] 输出:3 解释:2x2 网格如下: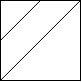
提示:
1 <= grid.length == grid[0].length <= 30grid[i][j]是'/'、'\'、或' '。
通过代码
官方题解
📺 视频讲解
力扣君温馨小贴士:觉得视频时间长的扣友,可以在视频右下角的「设置」按钮处选择 1.5 倍速或者 2 倍速观看。
📖 文字解析
这是一个关于连通性的问题,让我们求解连通分量的个数,解决这个问题没有特别的技巧,根据题意 画图分析、稍微细心一点就可以通过系统测评。
可以用深度优先遍历(Depth First Search)、广度优先遍历(Breadth First Search)和并查集(Disjoint Sets),由于只要求计算结果,不要求给出具体的连通信息,可以使用并查集。
方法:并查集
「斜杠」、「反斜杠」把单元格拆分成的 2 个三角形的形态,在做合并的时候需要分类讨论。根据「斜杠」、「反斜杠」分割的特点,我们把一个单元格分割成逻辑上的 4 个部分。如下图所示:
 {:width=500}
{:width=500}
我们须要遍历一次输入的二维网格 grid,在 单元格内 和 单元格间 进行合并。
单元格内:
- 如果是空格:合并 0、1、2、3;
- 如果是斜杠:合并 0、3,合并 1、2;
- 如果是反斜杠:合并 0、1,合并 2、3。
单元格间:
把每一个单元格拆分成 4 个小三角形以后,相邻的单元格须要合并,无须分类讨论。我们选择在遍历 grid 的每一个单元格的时候,分别「向右、向下」尝试合并。
 {:width=300}
{:width=300}
- 向右:合并 1 (当前单元格)和 3(当前单元格右边 1 列的单元格),上图中红色部分;
- 向下:合并 2 (当前单元格)和 0(当前单元格下边 1 列的单元格),上图中蓝色部分。
事实上,大家选择在遍历 grid 的每一个单元格的时候,分别「向左、向上」、「向左、向下」、「向右、向上」、「向右、向下」中的任何一种都可以。
合并完成以后,并查集里连通分量的个数就是题目要求的区域的个数。
参考代码:
[]public class Solution { public int regionsBySlashes(String[] grid) { int N = grid.length; int size = 4 * N * N; UnionFind unionFind = new UnionFind(size); for (int i = 0; i < N; i++) { char[] row = grid[i].toCharArray(); for (int j = 0; j < N; j++) { // 二维网格转换为一维表格,index 表示将单元格拆分成 4 个小三角形以后,编号为 0 的小三角形的在并查集中的下标 int index = 4 * (i * N + j); char c = row[j]; // 单元格内合并 if (c == '/') { // 合并 0、3,合并 1、2 unionFind.union(index, index + 3); unionFind.union(index + 1, index + 2); } else if (c == '\\') { // 合并 0、1,合并 2、3 unionFind.union(index, index + 1); unionFind.union(index + 2, index + 3); } else { unionFind.union(index, index + 1); unionFind.union(index + 1, index + 2); unionFind.union(index + 2, index + 3); } // 单元格间合并 // 向右合并:1(当前)、3(右一列) if (j + 1 < N) { unionFind.union(index + 1, 4 * (i * N + j + 1) + 3); } // 向下合并:2(当前)、0(下一行) if (i + 1 < N) { unionFind.union(index + 2, 4 * ((i + 1) * N + j)); } } } return unionFind.getCount(); } private class UnionFind { private int[] parent; private int count; public int getCount() { return count; } public UnionFind(int n) { this.count = n; this.parent = new int[n]; for (int i = 0; i < n; i++) { parent[i] = i; } } public int find(int x) { while (x != parent[x]) { parent[x] = parent[parent[x]]; x = parent[x]; } return x; } public void union(int x, int y) { int rootX = find(x); int rootY = find(y); if (rootX == rootY) { return; } parent[rootX] = rootY; count--; } } }
复杂度分析
- 时间复杂度:$O(N^2 \log N)$,其中 $N$ 是网格的长度,$O(N^2 \log N^2) = O(2N^2 \log N)$;
- 空间复杂度:$O(N^2)$。
本题采用了「先拆后合」的策略,避免了相对复杂的分类讨论。
统计信息
| 通过次数 | 提交次数 | AC比率 |
|---|---|---|
| 19956 | 26825 | 74.4% |
提交历史
| 提交时间 | 提交结果 | 执行时间 | 内存消耗 | 语言 |
|---|