973-最接近原点的 K 个点(K Closest Points to Origin)

原文链接: https://leetcode-cn.com/problems/k-closest-points-to-origin

英文原文

Given an array of points where points[i] = [x_i, y_i] represents a point on the X-Y plane and an integer k, return the k closest points to the origin (0, 0).

The distance between two points on the X-Y plane is the Euclidean distance (i.e., √(x₁ - x₂)² + (y₁ - y₂)²).

You may return the answer in any order. The answer is guaranteed to be unique (except for the order that it is in).

Example 1:

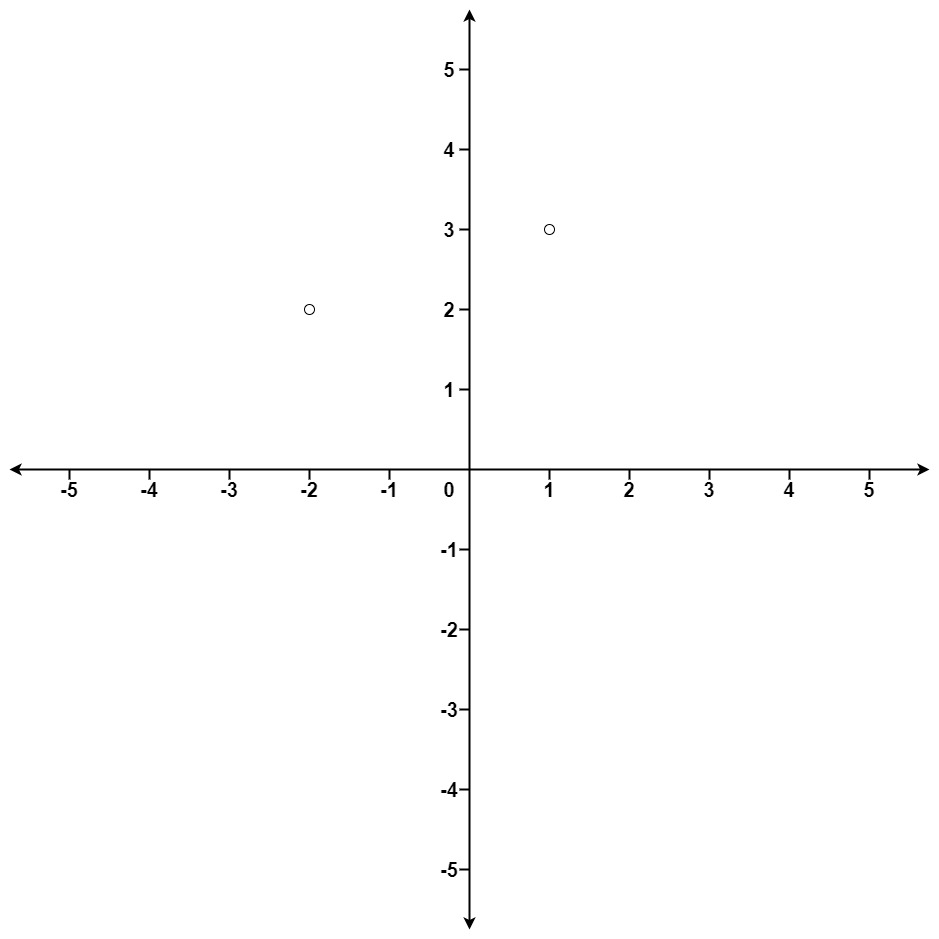
Input: points = [[1,3],[-2,2]], k = 1
Output: [[-2,2]]
Explanation:
The distance between (1, 3) and the origin is sqrt(10).
The distance between (-2, 2) and the origin is sqrt(8).
Since sqrt(8) < sqrt(10), (-2, 2) is closer to the origin.
We only want the closest k = 1 points from the origin, so the answer is just [[-2,2]].

Example 2:

Input: points = [[3,3],[5,-1],[-2,4]], k = 2
Output: [[3,3],[-2,4]]
Explanation: The answer [[-2,4],[3,3]] would also be accepted.

Constraints:

1 <= k <= points.length <= 10⁴
-10⁴ < x_i, y_i < 10⁴

中文题目

我们有一个由平面上的点组成的列表 points。需要从中找出 K 个距离原点 (0, 0) 最近的点。

（这里，平面上两点之间的距离是欧几里德距离。）

你可以按任何顺序返回答案。除了点坐标的顺序之外，答案确保是唯一的。

示例 1：

输入：points = [[1,3],[-2,2]], K = 1
输出：[[-2,2]]
解释： 
(1, 3) 和原点之间的距离为 sqrt(10)，
(-2, 2) 和原点之间的距离为 sqrt(8)，
由于 sqrt(8) < sqrt(10)，(-2, 2) 离原点更近。
我们只需要距离原点最近的 K = 1 个点，所以答案就是 [[-2,2]]。

示例 2：

输入：points = [[3,3],[5,-1],[-2,4]], K = 2
输出：[[3,3],[-2,4]]
（答案 [[-2,4],[3,3]] 也会被接受。）

提示：

1 <= K <= points.length <= 10000
-10000 < points[i][0] < 10000
-10000 < points[i][1] < 10000

通过代码

高赞题解

前言

当我们计算出每个点到原点的欧几里得距离的平方后，本题和「剑指 Offer 40. 最小的k个数」是完全一样的题。

为什么是欧几里得距离的「平方」？这是因为欧几里得距离并不一定是个整数，在进行计算和比较时可能会引进误差；但它的平方一定是个整数，这样我们就无需考虑误差了。

方法一：排序

思路和算法

将每个点到原点的欧几里得距离的平方从小到大排序后，取出前 $k$ 个即可。

代码

[sol1-C++]
class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        sort(points.begin(), points.end(), [](const vector<int>& u, const vector<int>& v) {
            return u[0] * u[0] + u[1] * u[1] < v[0] * v[0] + v[1] * v[1];
        });
        return {points.begin(), points.begin() + k};
    }
};

[sol1-Java]
class Solution {
    public int[][] kClosest(int[][] points, int k) {
        Arrays.sort(points, new Comparator<int[]>() {
            public int compare(int[] point1, int[] point2) {
                return (point1[0] * point1[0] + point1[1] * point1[1]) - (point2[0] * point2[0] + point2[1] * point2[1]);
            }
        });
        return Arrays.copyOfRange(points, 0, k);
    }
}

[sol1-Python3]
class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        points.sort(key=lambda x: (x[0] ** 2 + x[1] ** 2))
        return points[:k]

[sol1-Golang]
func kClosest(points [][]int, k int) [][]int {
    sort.Slice(points, func(i, j int) bool {
        p, q := points[i], points[j]
        return p[0]*p[0]+p[1]*p[1] < q[0]*q[0]+q[1]*q[1]
    })
    return points[:k]
}

[sol1-C]
int cmp(const void* _a, const void* _b) {
    int *a = *(int**)_a, *b = *(int**)_b;
    return a[0] * a[0] + a[1] * a[1] - b[0] * b[0] - b[1] * b[1];
}

int** kClosest(int** points, int pointsSize, int* pointsColSize, int k, int* returnSize, int** returnColumnSizes) {
    qsort(points, pointsSize, sizeof(int*), cmp);
    *returnSize = k;
    *returnColumnSizes = malloc(sizeof(int) * k);
    int** ret = malloc(sizeof(int*) * k);
    for (int i = 0; i < k; i++) {
        (*returnColumnSizes)[i] = 2;
        ret[i] = malloc(sizeof(int) * 2);
        ret[i][0] = points[i][0], ret[i][1] = points[i][1];
    }
    return ret;
}

复杂度分析

时间复杂度：$O(n\log n)$，其中 $n$ 是数组 $\textit{points}$ 的长度。算法的时间复杂度即排序的时间复杂度。
空间复杂度：$O(\log n)$，排序所需额外的空间复杂度为 $O(\log n)$。

方法二：堆

思路和算法

我们可以使用一个大根堆实时维护前 $k$ 个最小的距离平方。

首先我们将前 $k$ 个点的编号（为了方便最后直接得到答案）以及对应的距离平方放入大根堆中，随后从第 $k+1$ 个点开始遍历：如果当前点的距离平方比堆顶的点的距离平方要小，就把堆顶的点弹出，再插入当前的点。当遍历完成后，所有在大根堆中的点就是前 $k$ 个距离最小的点。

不同的语言提供的堆的默认情况不一定相同。在 C++ 语言中，堆（即优先队列）为大根堆，但在 Python 语言中，堆为小根堆，因此我们需要在小根堆中存储（以及比较）距离平方的相反数。

代码

[sol2-C++]
class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        priority_queue<pair<int, int>> q;
        for (int i = 0; i < k; ++i) {
            q.emplace(points[i][0] * points[i][0] + points[i][1] * points[i][1], i);
        }
        int n = points.size();
        for (int i = k; i < n; ++i) {
            int dist = points[i][0] * points[i][0] + points[i][1] * points[i][1];
            if (dist < q.top().first) {
                q.pop();
                q.emplace(dist, i);
            }
        }
        vector<vector<int>> ans;
        while (!q.empty()) {
            ans.push_back(points[q.top().second]);
            q.pop();
        }
        return ans;
    }
};

[sol2-Java]
class Solution {
    public int[][] kClosest(int[][] points, int k) {
        PriorityQueue<int[]> pq = new PriorityQueue<int[]>(new Comparator<int[]>() {
            public int compare(int[] array1, int[] array2) {
                return array2[0] - array1[0];
            }
        });
        for (int i = 0; i < k; ++i) {
            pq.offer(new int[]{points[i][0] * points[i][0] + points[i][1] * points[i][1], i});
        }
        int n = points.length;
        for (int i = k; i < n; ++i) {
            int dist = points[i][0] * points[i][0] + points[i][1] * points[i][1];
            if (dist < pq.peek()[0]) {
                pq.poll();
                pq.offer(new int[]{dist, i});
            }
        }
        int[][] ans = new int[k][2];
        for (int i = 0; i < k; ++i) {
            ans[i] = points[pq.poll()[1]];
        }
        return ans;
    }
}

[sol2-Python3]
class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        q = [(-x ** 2 - y ** 2, i) for i, (x, y) in enumerate(points[:k])]
        heapq.heapify(q)
        
        n = len(points)
        for i in range(k, n):
            x, y = points[i]
            dist = -x ** 2 - y ** 2
            heapq.heappushpop(q, (dist, i))
        
        ans = [points[identity] for (_, identity) in q]
        return ans

[sol2-Golang]
type pair struct {
    dist  int
    point []int
}
type hp []pair

func (h hp) Len() int            { return len(h) }
func (h hp) Less(i, j int) bool  { return h[i].dist > h[j].dist }
func (h hp) Swap(i, j int)       { h[i], h[j] = h[j], h[i] }
func (h *hp) Push(v interface{}) { *h = append(*h, v.(pair)) }
func (h *hp) Pop() interface{}   { a := *h; v := a[len(a)-1]; *h = a[:len(a)-1]; return v }

func kClosest(points [][]int, k int) (ans [][]int) {
    h := make(hp, k)
    for i, p := range points[:k] {
        h[i] = pair{p[0]*p[0] + p[1]*p[1], p}
    }
    heap.Init(&h) // O(k) 初始化堆
    for _, p := range points[k:] {
        if dist := p[0]*p[0] + p[1]*p[1]; dist < h[0].dist {
            h[0] = pair{dist, p}
            heap.Fix(&h, 0) // 效率比 pop 后 push 要快
        }
    }
    for _, p := range h {
        ans = append(ans, p.point)
    }
    return
}

复杂度分析

时间复杂度：$O(n\log k)$，其中 $n$ 是数组 $\textit{points}$ 的长度。由于大根堆维护的是前 $k$ 个距离最小的点，因此弹出和插入操作的单次时间复杂度均为 $O(\log k)$。在最坏情况下，数组里 $n$ 个点都会插入，因此时间复杂度为 $O(n\log k)$。
空间复杂度：$O(k)$，因为大根堆中最多有 $k$ 个点。

方法三：快速选择（快速排序的思想）

思路和算法

我们也可以借鉴快速排序的思想。

快速排序中的划分操作每次执行完后，都能将数组分成两个部分，其中小于等于分界值 $\textit{pivot}$ 的元素都会被放到左侧部分，而大于 $\textit{pivot}$ 的元素都都会被放到右侧部分。与快速排序不同的是，在本题中我们可以根据 $k$ 与 $\textit{pivot}$ 下标的位置关系，只处理划分结果的某一部分（而不是像快速排序一样需要处理两个部分）。

我们定义函数 random_select(left, right, k) 表示划分数组 $\textit{points}$ 的 $[\textit{left},\textit{right}]$ 区间，并且需要找到其中第 $k$ 个距离最小的点。在一次划分操作完成后，设 $\textit{pivot}$ 的下标为 $i$，即区间 $[\textit{left}, i-1]$ 中的点的距离都小于等于 $\textit{pivot}$，而区间 $[i+1,\textit{right}]$ 的点的距离都大于 $\textit{pivot}$。此时会有三种情况：

如果 $k = i-\textit{left}+1$，那么说明 $\textit{pivot}$ 就是第 $k$ 个距离最小的点，我们可以结束整个过程；
如果 $k < i-\textit{left}+1$，那么说明第 $k$ 个距离最小的点在 $\textit{pivot}$ 左侧，因此递归调用 random_select(left, i - 1, k)；
如果 $k > i-\textit{left}+1$，那么说明第 $k$ 个距离最小的点在 $\textit{pivot}$ 右侧，因此递归调用 random_select(i + 1, right, k - (i - left + 1))。

在整个过程结束之后，第 $k$ 个距离最小的点恰好就在数组 $\textit{points}$ 中的第 $k$ 个位置，并且其左侧的所有点的距离都小于它。此时，我们就找到了前 $k$ 个距离最小的点。

代码

[sol3-C++]
class Solution {
private:
    mt19937 gen{random_device{}()};

public:
    void random_select(vector<vector<int>>& points, int left, int right, int k) {
        int pivot_id = uniform_int_distribution<int>{left, right}(gen);
        int pivot = points[pivot_id][0] * points[pivot_id][0] + points[pivot_id][1] * points[pivot_id][1];
        swap(points[right], points[pivot_id]);
        int i = left - 1;
        for (int j = left; j < right; ++j) {
            int dist = points[j][0] * points[j][0] + points[j][1] * points[j][1];
            if (dist <= pivot) {
                ++i;
                swap(points[i], points[j]);
            }
        }
        ++i;
        swap(points[i], points[right]);
        // [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
        if (k < i - left + 1) {
            random_select(points, left, i - 1, k);
        }
        else if (k > i - left + 1) {
            random_select(points, i + 1, right, k - (i - left + 1));
        }
    }

    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        int n = points.size();
        random_select(points, 0, n - 1, k);
        return {points.begin(), points.begin() + k};
    }
};

[sol3-C++api]
class Solution {
public:
    vector<vector<int>> kClosest(vector<vector<int>>& points, int k) {
        nth_element(points.begin(), points.begin() + k - 1, points.end(), [](const vector<int>& u, const vector<int>& v) {
            return u[0] * u[0] + u[1] * u[1] < v[0] * v[0] + v[1] * v[1];
        });
        return {points.begin(), points.begin() + k};
    }
};

[sol3-Java]
class Solution {
    Random rand = new Random();

    public int[][] kClosest(int[][] points, int k) {
        int n = points.length;
        random_select(points, 0, n - 1, k);
        return Arrays.copyOfRange(points, 0, k);
    }

    public void random_select(int[][] points, int left, int right, int k) {
        int pivotId = left + rand.nextInt(right - left + 1);
        int pivot = points[pivotId][0] * points[pivotId][0] + points[pivotId][1] * points[pivotId][1];
        swap(points, right, pivotId);
        int i = left - 1;
        for (int j = left; j < right; ++j) {
            int dist = points[j][0] * points[j][0] + points[j][1] * points[j][1];
            if (dist <= pivot) {
                ++i;
                swap(points, i, j);
            }
        }
        ++i;
        swap(points, i, right);
        // [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
        if (k < i - left + 1) {
            random_select(points, left, i - 1, k);
        } else if (k > i - left + 1) {
            random_select(points, i + 1, right, k - (i - left + 1));
        }
    }

    public void swap(int[][] points, int index1, int index2) {
        int[] temp = points[index1];
        points[index1] = points[index2];
        points[index2] = temp;
    }
}

[sol3-Python]
class Solution:
    def kClosest(self, points: List[List[int]], k: int) -> List[List[int]]:
        def random_select(left: int, right: int, k: int):
            pivot_id = random.randint(left, right)
            pivot = points[pivot_id][0] ** 2 + points[pivot_id][1] ** 2
            points[right], points[pivot_id] = points[pivot_id], points[right]
            i = left - 1
            for j in range(left, right):
                if points[j][0] ** 2 + points[j][1] ** 2 <= pivot:
                    i += 1
                    points[i], points[j] = points[j], points[i]
            i += 1
            points[i], points[right] = points[right], points[i]
            # [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
            if k < i - left + 1:
                random_select(left, i - 1, k)
            elif k > i - left + 1:
                random_select(i + 1, right, k - (i - left + 1))

        n = len(points)
        random_select(0, n - 1, k)
        return points[:k]

[sol3-Golang]
func less(p, q []int) bool {
    return p[0]*p[0]+p[1]*p[1] < q[0]*q[0]+q[1]*q[1]
}

func kClosest(points [][]int, k int) (ans [][]int) {
    rand.Shuffle(len(points), func(i, j int) {
        points[i], points[j] = points[j], points[i]
    })

    var quickSelect func(left, right int)
    quickSelect = func(left, right int) {
        if left == right {
            return
        }
        pivot := points[right] // 取当前区间 [left,right] 最右侧元素作为切分参照
        lessCount := left
        for i := left; i < right; i++ {
            if less(points[i], pivot) {
                points[i], points[lessCount] = points[lessCount], points[i]
                lessCount++
            }
        }
        // 循环结束后，有 lessCount 个元素比 pivot 小
        // 把 pivot 交换到 points[lessCount] 的位置
        // 交换之后，points[lessCount] 左侧的元素均小于 pivot，points[lessCount] 右侧的元素均不小于 pivot
        points[right], points[lessCount] = points[lessCount], points[right]
        if lessCount+1 == k {
            return
        } else if lessCount+1 < k {
            quickSelect(lessCount+1, right)
        } else {
            quickSelect(left, lessCount-1)
        }
    }
    quickSelect(0, len(points)-1)
    return points[:k]
}

[sol3-C]
void swap(int** a, int** b) {
    int* t = *a;
    *a = *b, *b = t;
}

void random_select(int** points, int left, int right, int k) {
    int pivot_id = rand() % (right - left + 1) + left;
    int pivot = points[pivot_id][0] * points[pivot_id][0] + points[pivot_id][1] * points[pivot_id][1];
    swap(points[right], points[pivot_id]);
    int i = left - 1;
    for (int j = left; j < right; ++j) {
        int dist = points[j][0] * points[j][0] + points[j][1] * points[j][1];
        if (dist <= pivot) {
            ++i;
            swap(&points[i], &points[j]);
        }
    }
    ++i;
    swap(&points[i], &points[right]);
    // [left, i-1] 都小于等于 pivot, [i+1, right] 都大于 pivot
    if (k < i - left + 1) {
        random_select(points, left, i - 1, k);
    } else if (k > i - left + 1) {
        random_select(points, i + 1, right, k - (i - left + 1));
    }
}

int** kClosest(int** points, int pointsSize, int* pointsColSize, int k, int* returnSize, int** returnColumnSizes) {
    srand(time(0));
    random_select(points, 0, pointsSize - 1, k);
    *returnSize = k;
    *returnColumnSizes = malloc(sizeof(int) * k);
    int** ret = malloc(sizeof(int*) * k);
    for (int i = 0; i < k; i++) {
        (*returnColumnSizes)[i] = 2;
        ret[i] = malloc(sizeof(int) * 2);
        ret[i][0] = points[i][0], ret[i][1] = points[i][1];
    }
    return ret;
}

复杂度分析

时间复杂度：期望为 $O(n)$，其中 $n$ 是数组 $\textit{points}$ 的长度。由于证明过程很繁琐，所以不在这里展开讲。具体证明可以参考《算法导论》第 9 章第 2 小节。

最坏情况下，时间复杂度为 $O(n^2)$。具体地，每次的划分点都是最大值或最小值，一共需要划分 $n-1$ 次，而一次划分需要线性的时间复杂度，所以最坏情况下时间复杂度为 $O(n^2)$。
空间复杂度：期望为 $O(\log n)$，即为递归调用的期望深度。

最坏情况下，空间复杂度为 $O(n)$，此时需要划分 $n-1$ 次，对应递归的深度为 $n-1$ 层，所以最坏情况下时间复杂度为 $O(n)$。

然而注意到代码中的递归都是「尾递归」，因此如果编译器支持尾递归优化，那么空间复杂度总为 $O(1)$。即使不支持尾递归优化，我们也可以很方便地将上面的代码改成循环迭代的写法。

统计信息

通过次数	提交次数	AC比率
70095	109178	64.2%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
数组中的第K个最大元素	中等
前 K 个高频元素	中等
前K个高频单词	中等

凤起丶宛南

从来没有真正的绝境，只有心灵的迷途

英文原文

中文题目

通过代码

高赞题解

前言

方法一：排序

方法二：堆

方法三：快速选择（快速排序的思想）

统计信息

提交历史

相似题目

你的赏识是我前进的动力