原文链接: https://leetcode-cn.com/problems/distribute-coins-in-binary-tree

英文原文

You are given the root of a binary tree with n nodes where each node in the tree has node.val coins. There are n coins in total throughout the whole tree.

In one move, we may choose two adjacent nodes and move one coin from one node to another. A move may be from parent to child, or from child to parent.

Return the minimum number of moves required to make every node have exactly one coin.

 

Example 1:

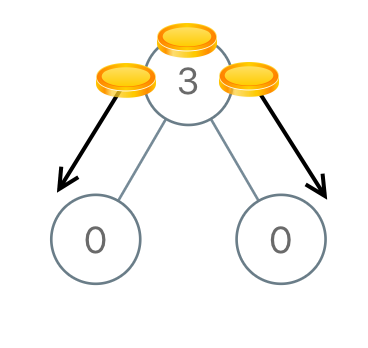
Input: root = [3,0,0]
Output: 2
Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.

Example 2:

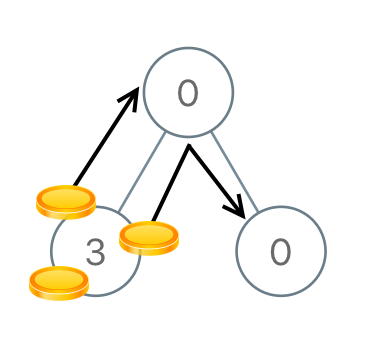
Input: root = [0,3,0]
Output: 3
Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.

Example 3:

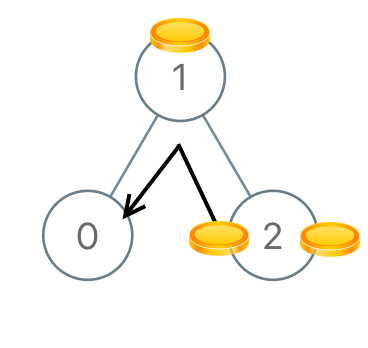
Input: root = [1,0,2]
Output: 2

Example 4:

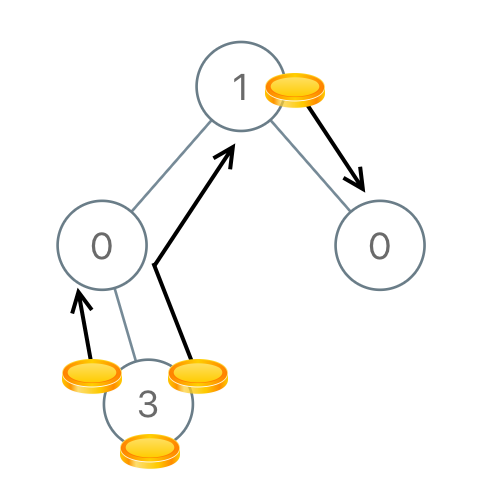
Input: root = [1,0,0,null,3]
Output: 4

 

Constraints:

• The number of nodes in the tree is n.
• 1 <= n <= 100
• 0 <= Node.val <= n
• The sum of all Node.val is n.

中文题目

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点。)。

返回使每个结点上只有一枚硬币所需的移动次数。

 

示例 1：

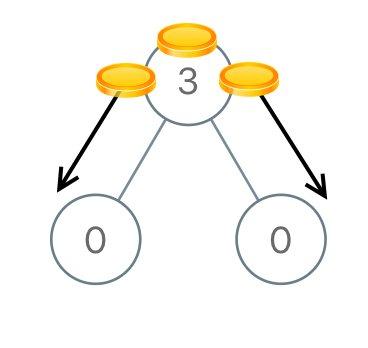
输入：[3,0,0]
输出：2
解释：从树的根结点开始，我们将一枚硬币移到它的左子结点上，一枚硬币移到它的右子结点上。

示例 2：

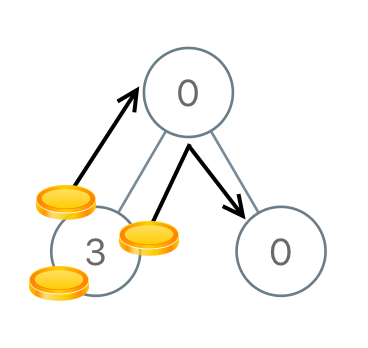
输入：[0,3,0]
输出：3
解释：从根结点的左子结点开始，我们将两枚硬币移到根结点上 [移动两次]。然后，我们把一枚硬币从根结点移到右子结点上。

示例 3：

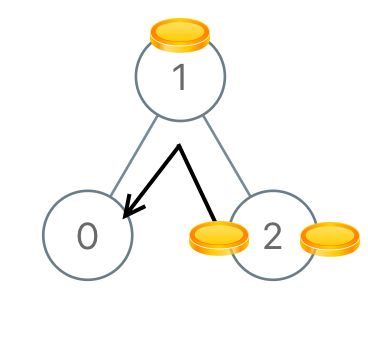
输入：[1,0,2]
输出：2

示例 4：

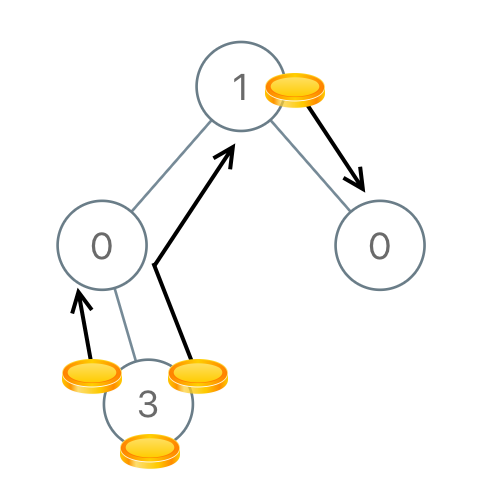
输入：[1,0,0,null,3]
输出：4

 

提示：

1. 1<= N <= 100
2. 0 <= node.val <= N

通过代码

官方题解

方法：深度优先搜索

思路

如果树的叶子仅包含 0 枚金币（与它所需相比，它的 过载量 为 -1），那么我们需要从它的父亲节点移动一枚金币到这个叶子节点上。如果说，一个叶子节点包含 4 枚金币（它的 过载量 为 3），那么我们需要将这个叶子节点中的 3 枚金币移动到别的地方去。总的来说，对于一个叶子节点，需要移动到它中或需要从它移动到它的父亲中的金币数量为 过载量 = Math.abs(num_coins - 1)。然后，在接下来的计算中，我们就再也不需要考虑这些已经考虑过的叶子节点了。

算法

我们可以用上述的方法来逐步构建我们的最终答案。定义 dfs(node) 为这个节点所在的子树中金币的 过载量，也就是这个子树中金币的数量减去这个子树中节点的数量。接着，我们可以计算出这个节点与它的子节点之间需要移动金币的数量为 abs(dfs(node.left)) + abs(dfs(node.right))，这个节点金币的过载量为 node.val + dfs(node.left) + dfs(node.right) - 1。

[u7ECkcHs-Java]
class Solution {
    int ans;
    public int distributeCoins(TreeNode root) {
        ans = 0;
        dfs(root);
        return ans;
    }

    public int dfs(TreeNode node) {
        if (node == null) return 0;
        int L = dfs(node.left);
        int R = dfs(node.right);
        ans += Math.abs(L) + Math.abs(R);
        return node.val + L + R - 1;
    }
}

[u7ECkcHs-Python]
class Solution(object):
    def distributeCoins(self, root):
        self.ans = 0

        def dfs(node):
            if not node: return 0
            L, R = dfs(node.left), dfs(node.right)
            self.ans += abs(L) + abs(R)
            return node.val + L + R - 1

        dfs(root)
        return self.ans

复杂度分析

• 时间复杂度：$O(N)$，其中 $N$ 是给定树中节点的数量。

• 空间复杂度：$O(H)$，其中 $H$ 给定树的高度。

统计信息

通过次数	提交次数	AC比率
8865	12420	71.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
树中距离之和	困难
监控二叉树	困难