原文链接: https://leetcode-cn.com/problems/smallest-string-starting-from-leaf

英文原文

You are given the root of a binary tree where each node has a value in the range [0, 25] representing the letters 'a' to 'z'.

Return the lexicographically smallest string that starts at a leaf of this tree and ends at the root.

As a reminder, any shorter prefix of a string is lexicographically smaller.

• For example, "ab" is lexicographically smaller than "aba".

A leaf of a node is a node that has no children.

 

Example 1:

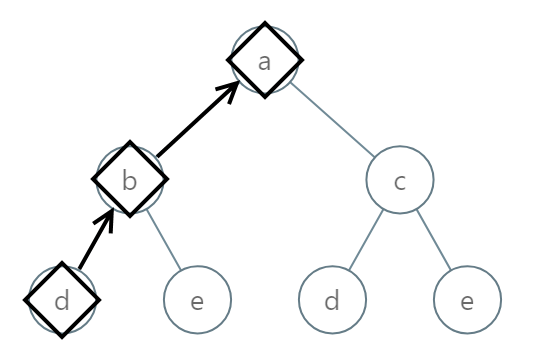
Input: root = [0,1,2,3,4,3,4]
Output: "dba"

Example 2:

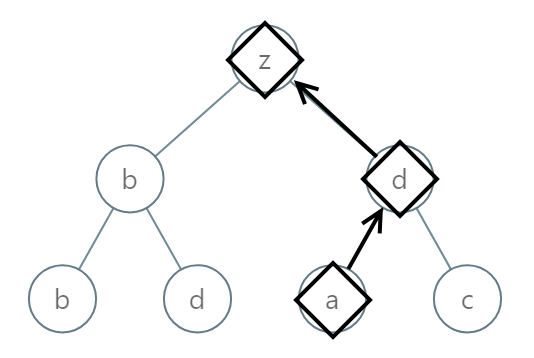
Input: root = [25,1,3,1,3,0,2]
Output: "adz"

Example 3:

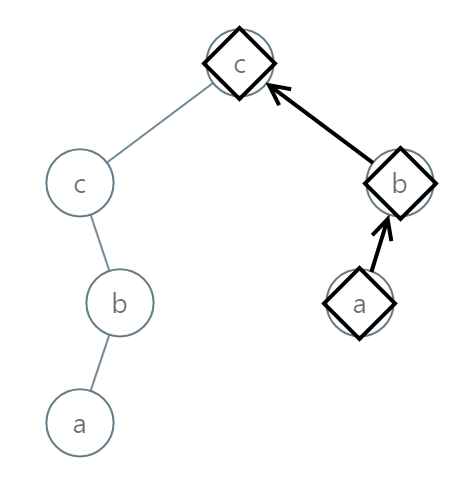
Input: root = [2,2,1,null,1,0,null,0]
Output: "abc"

 

Constraints:

• The number of nodes in the tree is in the range [1, 8500].
• 0 <= Node.val <= 25

中文题目

给定一颗根结点为 root 的二叉树，树中的每一个结点都有一个从 0 到 25 的值，分别代表字母 'a' 到 'z'：值 0 代表 'a'，值 1 代表 'b'，依此类推。

找出按字典序最小的字符串，该字符串从这棵树的一个叶结点开始，到根结点结束。

（小贴士：字符串中任何较短的前缀在字典序上都是较小的：例如，在字典序上 "ab" 比 "aba" 要小。叶结点是指没有子结点的结点。）

 

示例 1：

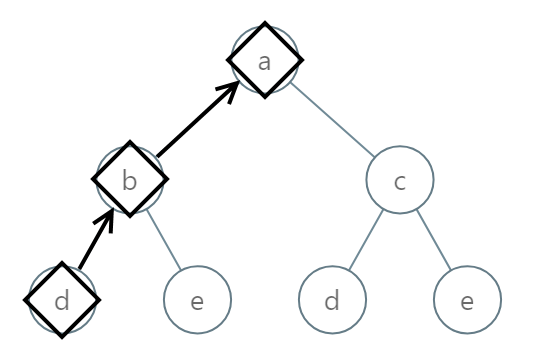
输入：[0,1,2,3,4,3,4]
输出："dba"

示例 2：

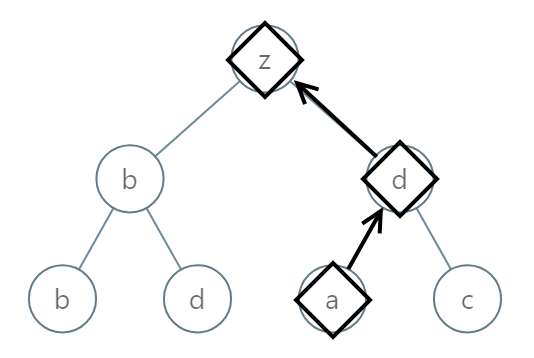
输入：[25,1,3,1,3,0,2]
输出："adz"

示例 3：

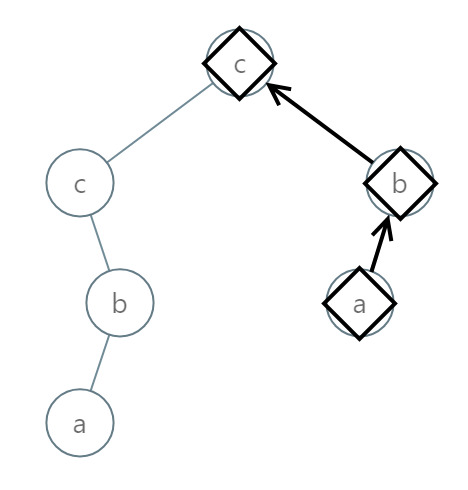
输入：[2,2,1,null,1,0,null,0]
输出："abc"

 

提示：

1. 给定树的结点数介于 1 和 8500 之间。
2. 树中的每个结点都有一个介于 0 和 25 之间的值。

通过代码

官方题解

方法：暴力法

思路

让我们创建出所有可能的字符串，然后逐一比较，输出字典序最小的那个。

算法

在我们深度优先搜索的过程中，我们不断调整 sb（或者 Python 代码中的 A），即根到这个节点的路径上的字符串内容。

当我们到达一个叶子节点的时候，我们翻转路径的字符串内容来创建一个候选答案。如果候选答案比当前答案要优秀，那么我们更新答案。

[deze3qTk-Java]
class Solution {
    String ans = "~";
    public String smallestFromLeaf(TreeNode root) {
        dfs(root, new StringBuilder());
        return ans;
    }

    public void dfs(TreeNode node, StringBuilder sb) {
        if (node == null) return;
        sb.append((char)('a' + node.val));

        if (node.left == null && node.right == null) {
            sb.reverse();
            String S = sb.toString();
            sb.reverse();

            if (S.compareTo(ans) < 0)
                ans = S;
        }

        dfs(node.left, sb);
        dfs(node.right, sb);
        sb.deleteCharAt(sb.length() - 1);
    }
}

[deze3qTk-Python]
class Solution(object):
    def smallestFromLeaf(self, root):
        self.ans = "~"

        def dfs(node, A):
            if node:
                A.append(chr(node.val + ord('a')))
                if not node.left and not node.right:
                    self.ans = min(self.ans, "".join(reversed(A)))

                dfs(node.left, A)
                dfs(node.right, A)
                A.pop()

        dfs(root, [])
        return self.ans

复杂度分析

• 时间复杂度：我们用 $O(N)$ 遍历这棵树，然后调整字符串内容 A [Python] 或者 sb。然后，翻转与比较的时间复杂度为 $O(L)$，其中 $L$ 是到达叶节点时候得到字符串的长度。例如，对于完全平衡的树，$L = \log N$ 且时间复杂度为 $O(N \log N)$。

• 空间复杂度：$O(N)$。

统计信息

通过次数	提交次数	AC比率
9855	19685	50.1%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言

相似题目

题目	难度
求根节点到叶节点数字之和	中等
二叉树的所有路径	简单