990-等式方程的可满足性(Satisfiability of Equality Equations)
发表于：2021-12-03 | 分类： 中等
字数统计: 1.9k | 阅读时长: 9分钟 | 阅读量：

原文链接: https://leetcode-cn.com/problems/satisfiability-of-equality-equations

英文原文

You are given an array of strings equations that represent relationships between variables where each string equations[i] is of length 4 and takes one of two different forms: "xi==yi" or "xi!=yi".Here, xi and yi are lowercase letters (not necessarily different) that represent one-letter variable names.

Return true if it is possible to assign integers to variable names so as to satisfy all the given equations, or false otherwise.

 

Example 1:

Input: equations = ["a==b","b!=a"]
Output: false
Explanation: If we assign say, a = 1 and b = 1, then the first equation is satisfied, but not the second.
There is no way to assign the variables to satisfy both equations.

Example 2:

Input: equations = ["b==a","a==b"]
Output: true
Explanation: We could assign a = 1 and b = 1 to satisfy both equations.

Example 3:

Input: equations = ["a==b","b==c","a==c"]
Output: true

Example 4:

Input: equations = ["a==b","b!=c","c==a"]
Output: false

Example 5:

Input: equations = ["c==c","b==d","x!=z"]
Output: true

 

Constraints:

  • 1 <= equations.length <= 500
  • equations[i].length == 4
  • equations[i][0] is a lowercase letter.
  • equations[i][1] is either '=' or '!'.
  • equations[i][2] is '='.
  • equations[i][3] is a lowercase letter.

中文题目

给定一个由表示变量之间关系的字符串方程组成的数组，每个字符串方程 equations[i] 的长度为 4，并采用两种不同的形式之一："a==b" 或 "a!=b"。在这里，a 和 b 是小写字母（不一定不同），表示单字母变量名。

只有当可以将整数分配给变量名，以便满足所有给定的方程时才返回 true，否则返回 false。 

 

示例 1：

输入：["a==b","b!=a"]
输出：false
解释：如果我们指定，a = 1 且 b = 1，那么可以满足第一个方程，但无法满足第二个方程。没有办法分配变量同时满足这两个方程。

示例 2：

输入：["b==a","a==b"]
输出：true
解释：我们可以指定 a = 1 且 b = 1 以满足满足这两个方程。

示例 3：

输入：["a==b","b==c","a==c"]
输出：true

示例 4：

输入：["a==b","b!=c","c==a"]
输出：false

示例 5：

输入：["c==c","b==d","x!=z"]
输出：true

 

提示：

  1. 1 <= equations.length <= 500
  2. equations[i].length == 4
  3. equations[i][0] 和 equations[i][3] 是小写字母
  4. equations[i][1] 要么是 '='，要么是 '!'
  5. equations[i][2] 是 '='

通过代码

高赞题解

📺 视频题解

990. 等式方程的可满足性.mp4

📖 文字题解

方法一：并查集

我们可以将每一个变量看作图中的一个节点，把相等的关系 == 看作是连接两个节点的边，那么由于表示相等关系的等式方程具有传递性，即如果 a==b 和 b==c 成立，则 a==c 也成立。也就是说，所有相等的变量属于同一个连通分量。因此，我们可以使用并查集来维护这种连通分量的关系。

首先遍历所有的等式，构造并查集。同一个等式中的两个变量属于同一个连通分量，因此将两个变量进行合并。

然后遍历所有的不等式。同一个不等式中的两个变量不能属于同一个连通分量，因此对两个变量分别查找其所在的连通分量，如果两个变量在同一个连通分量中，则产生矛盾，返回 false。

如果遍历完所有的不等式没有发现矛盾，则返回 true。

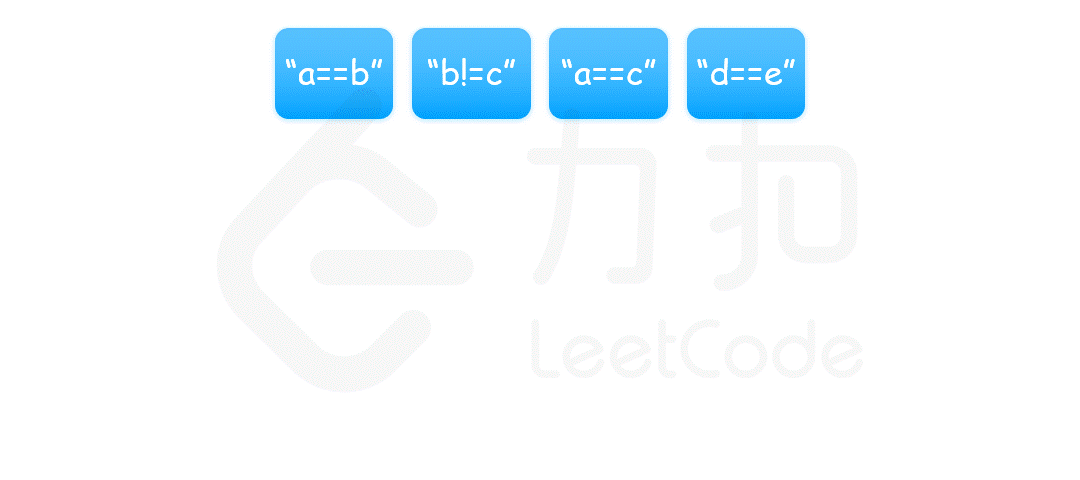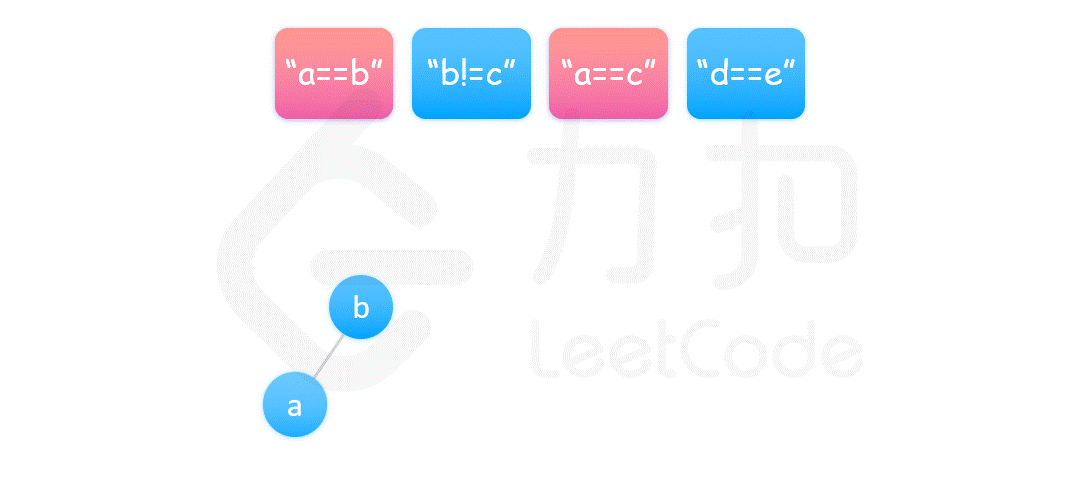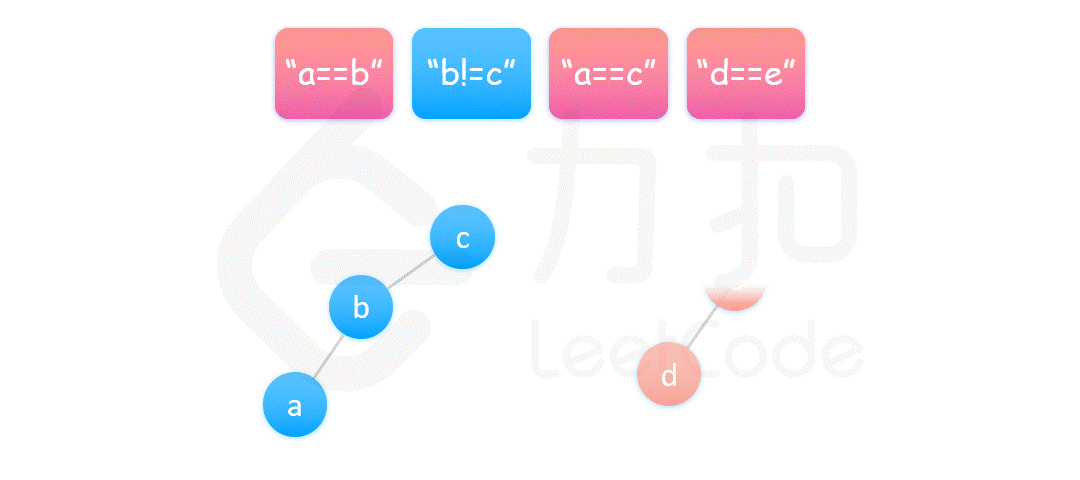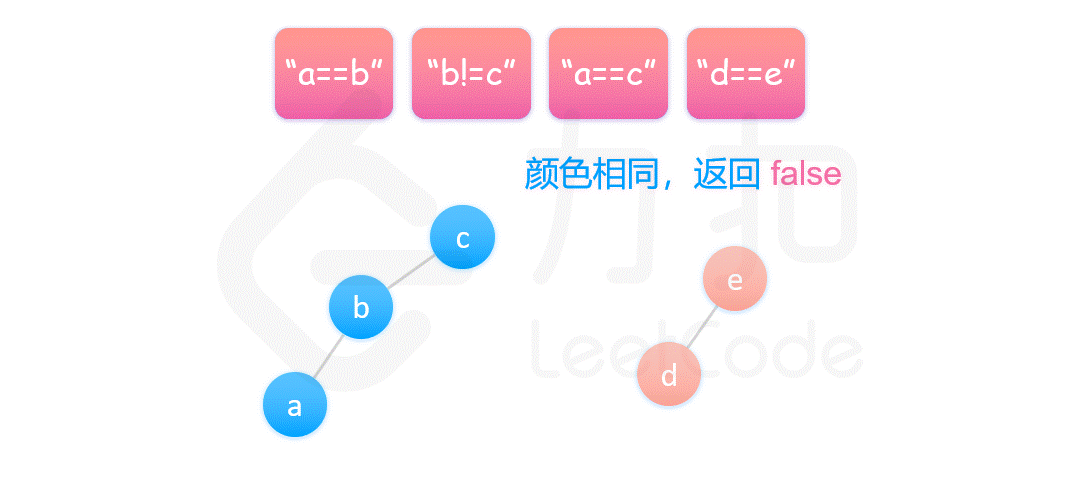fig1{:width=”90%”}

具体实现方面，使用一个数组 parent 存储每个变量的连通分量信息，其中的每个元素表示当前变量所在的连通分量的父节点信息，如果父节点是自身，说明该变量为所在的连通分量的根节点。一开始所有变量的父节点都是它们自身。对于合并操作，我们将第一个变量的根节点的父节点指向第二个变量的根节点；对于查找操作，我们沿着当前变量的父节点一路向上查找，直到找到根节点。

[sol1-Java]
class Solution {
    public boolean equationsPossible(String[] equations) {
        int[] parent = new int[26];
        for (int i = 0; i < 26; i++) {
            parent[i] = i;
        }
        for (String str : equations) {
            if (str.charAt(1) == '=') {
                int index1 = str.charAt(0) - 'a';
                int index2 = str.charAt(3) - 'a';
                union(parent, index1, index2);
            }
        }
        for (String str : equations) {
            if (str.charAt(1) == '!') {
                int index1 = str.charAt(0) - 'a';
                int index2 = str.charAt(3) - 'a';
                if (find(parent, index1) == find(parent, index2)) {
                    return false;
                }
            }
        }
        return true;
    }

    public void union(int[] parent, int index1, int index2) {
        parent[find(parent, index1)] = find(parent, index2);
    }

    public int find(int[] parent, int index) {
        while (parent[index] != index) {
            parent[index] = parent[parent[index]];
            index = parent[index];
        }
        return index;
    }
}
[sol1-C++]
class UnionFind {
private:
    vector<int> parent;

public:
    UnionFind() {
        parent.resize(26);
        iota(parent.begin(), parent.end(), 0);
    }

    int find(int index) {
        if (index == parent[index]) {
            return index;
        }
        parent[index] = find(parent[index]);
        return parent[index];
    }

    void unite(int index1, int index2) {
        parent[find(index1)] = find(index2);
    }
};

class Solution {
public:
    bool equationsPossible(vector<string>& equations) {
        UnionFind uf;
        for (const string& str: equations) {
            if (str[1] == '=') {
                int index1 = str[0] - 'a';
                int index2 = str[3] - 'a';
                uf.unite(index1, index2);
            }
        }
        for (const string& str: equations) {
            if (str[1] == '!') {
                int index1 = str[0] - 'a';
                int index2 = str[3] - 'a';
                if (uf.find(index1) == uf.find(index2)) {
                    return false;
                }
            }
        }
        return true;
    }
};
[sol1-Python3]
class Solution:

    class UnionFind:
        def __init__(self):
            self.parent = list(range(26))
        
        def find(self, index):
            if index == self.parent[index]:
                return index
            self.parent[index] = self.find(self.parent[index])
            return self.parent[index]
        
        def union(self, index1, index2):
            self.parent[self.find(index1)] = self.find(index2)


    def equationsPossible(self, equations: List[str]) -> bool:
        uf = Solution.UnionFind()
        for st in equations:
            if st[1] == "=":
                index1 = ord(st[0]) - ord("a")
                index2 = ord(st[3]) - ord("a")
                uf.union(index1, index2)
        for st in equations:
            if st[1] == "!":
                index1 = ord(st[0]) - ord("a")
                index2 = ord(st[3]) - ord("a")
                if uf.find(index1) == uf.find(index2):
                    return False
        return True
[sol1-Golang]
func equationsPossible(equations []string) bool {
    parent := make([]int, 26)
    for i := 0; i < 26; i++ {
        parent[i] = i
    }
    for _, str := range equations {
        if str[1] == '=' {
            index1 := int(str[0] - 'a')
            index2 := int(str[3] - 'a')
            union(parent, index1, index2)
        }
    }

    for _, str := range equations {
        if str[1] == '!' {
            index1 := int(str[0] - 'a')
            index2 := int(str[3] - 'a')
            if find(parent, index1) == find(parent, index2) {
                return false
            }
        }
    }
    return true
}

func union(parent []int, index1, index2 int) {
    parent[find(parent, index1)] = find(parent, index2)
}

func find(parent []int, index int) int {
    for parent[index] != index {
        parent[index] = parent[parent[index]]
        index = parent[index]
    }
    return index
}

复杂度分析

  • 时间复杂度：$O(n+C \log C)$，其中 $n$ 是 equations 中的方程数量，$C$ 是变量的总数，在本题中变量都是小写字母，即 $C \leq 26$。上面的并查集代码中使用了路径压缩优化，对于每个方程的合并和查找的均摊时间复杂度都是 $O(\log C)$。由于需要遍历每个方程，因此总时间复杂度是 $O(n+C \log C)$。

  • 空间复杂度：$O(C)$。创建一个数组 parent 存储每个变量的连通分量信息，由于变量都是小写字母，因此 parent 是长度为 $C$。

统计信息

通过次数 提交次数 AC比率
34945 68906 50.7%

提交历史

提交时间 提交结果 执行时间 内存消耗 语言
字符串 数组 图 并查集
上一篇:
988-从叶结点开始的最小字符串(Smallest String Starting From Leaf)
下一篇:
989-数组形式的整数加法(Add to Array-Form of Integer)
本文目录
本文目录
    •
    本站总访问量： 次 |
    Copyright © 2020 - 2021 枫奇丶宛南 | Powered by Hexo | Theme Bamboo