原文链接: https://leetcode-cn.com/problems/er-cha-sou-suo-shu-yu-shuang-xiang-lian-biao-lcof

中文题目

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点，只能调整树中节点指针的指向。

 

为了让您更好地理解问题，以下面的二叉搜索树为例：

 

 

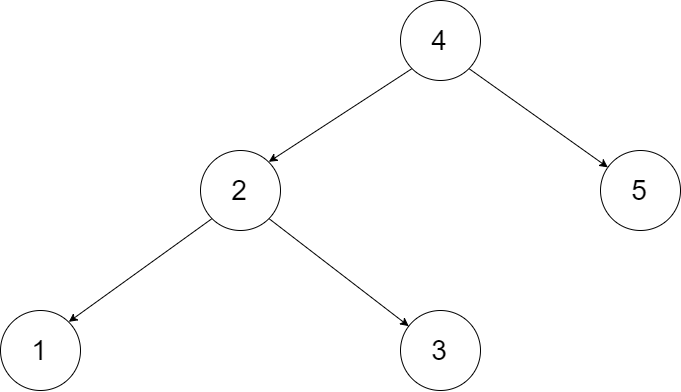
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表，第一个节点的前驱是最后一个节点，最后一个节点的后继是第一个节点。

下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。

 

 

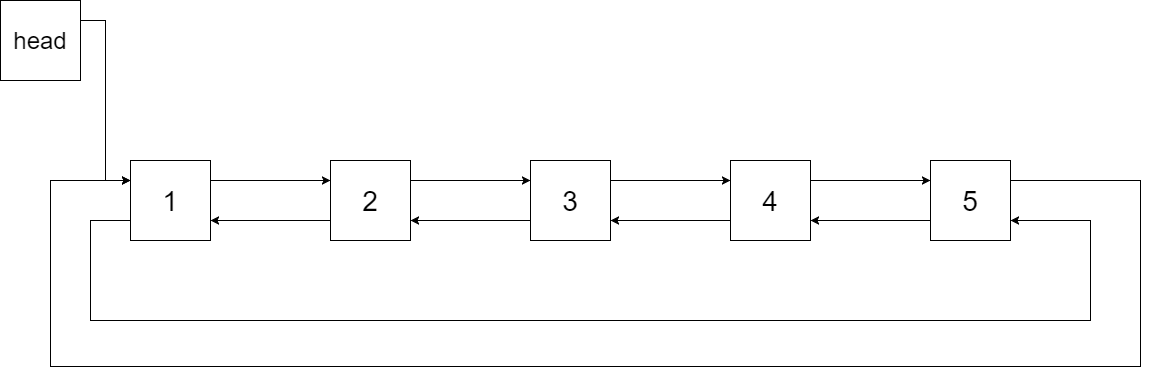
特别地，我们希望可以就地完成转换操作。当转化完成以后，树中节点的左指针需要指向前驱，树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。

 

注意：本题与主站 426 题相同：https://leetcode-cn.com/problems/convert-binary-search-tree-to-sorted-doubly-linked-list/

注意：此题对比原题有改动。

通过代码

高赞题解

解题思路：

本文解法基于性质：二叉搜索树的中序遍历为 递增序列 。
将 二叉搜索树 转换成一个 “排序的循环双向链表” ，其中包含三个要素：

1. 排序链表： 节点应从小到大排序，因此应使用 中序遍历 “从小到大”访问树的节点。
2. 双向链表： 在构建相邻节点的引用关系时，设前驱节点 pre 和当前节点 cur ，不仅应构建 pre.right = cur ，也应构建 cur.left = pre 。
3. 循环链表： 设链表头节点 head 和尾节点 tail ，则应构建 head.left = tail 和 tail.right = head 。

{:width=500}

中序遍历 为对二叉树作 “左、根、右” 顺序遍历，递归实现如下：

[]
# 打印中序遍历
def dfs(root):
    if not root: return
    dfs(root.left)  # 左
    print(root.val) # 根
    dfs(root.right) # 右

[]
// 打印中序遍历
void dfs(Node root) {
    if(root == null) return;
    dfs(root.left); // 左
    System.out.println(root.val); // 根
    dfs(root.right); // 右
}

[]
// 打印中序遍历
void dfs(Node* root) {
    if(root == nullptr) return;
    dfs(root->left); // 左
    cout << root->val << endl; // 根
    dfs(root->right); // 右
}

根据以上分析，考虑使用中序遍历访问树的各节点 cur ；并在访问每个节点时构建 cur 和前驱节点 pre 的引用指向；中序遍历完成后，最后构建头节点和尾节点的引用指向即可。

算法流程：

dfs(cur): 递归法中序遍历；

1. 终止条件： 当节点 cur 为空，代表越过叶节点，直接返回；
2. 递归左子树，即 dfs(cur.left) ；
3. 构建链表：
   1. 当 pre 为空时： 代表正在访问链表头节点，记为 head ；
   2. 当 pre 不为空时： 修改双向节点引用，即 pre.right = cur ， cur.left = pre ；
   3. 保存 cur ： 更新 pre = cur ，即节点 cur 是后继节点的 pre ；
4. 递归右子树，即 dfs(cur.right) ；

treeToDoublyList(root)：

1. 特例处理： 若节点 root 为空，则直接返回；
2. 初始化： 空节点 pre ；
3. 转化为双向链表： 调用 dfs(root) ；
4. 构建循环链表： 中序遍历完成后，head 指向头节点， pre 指向尾节点，因此修改 head 和 pre 的双向节点引用即可；
5. 返回值： 返回链表的头节点 head 即可；

<,,,,,,,,,,,,,>

复杂度分析：

• 时间复杂度 $O(N)$ ： $N$ 为二叉树的节点数，中序遍历需要访问所有节点。
• 空间复杂度 $O(N)$ ： 最差情况下，即树退化为链表时，递归深度达到 $N$，系统使用 $O(N)$ 栈空间。

代码：

[]
class Solution:
    def treeToDoublyList(self, root: 'Node') -> 'Node':
        def dfs(cur):
            if not cur: return
            dfs(cur.left) # 递归左子树
            if self.pre: # 修改节点引用
                self.pre.right, cur.left = cur, self.pre
            else: # 记录头节点
                self.head = cur
            self.pre = cur # 保存 cur
            dfs(cur.right) # 递归右子树
        
        if not root: return
        self.pre = None
        dfs(root)
        self.head.left, self.pre.right = self.pre, self.head
        return self.head

[]
class Solution {
    Node pre, head;
    public Node treeToDoublyList(Node root) {
        if(root == null) return null;
        dfs(root);
        head.left = pre;
        pre.right = head;
        return head;
    }
    void dfs(Node cur) {
        if(cur == null) return;
        dfs(cur.left);
        if(pre != null) pre.right = cur;
        else head = cur;
        cur.left = pre;
        pre = cur;
        dfs(cur.right);
    }
}

[]
class Solution {
public:
    Node* treeToDoublyList(Node* root) {
        if(root == nullptr) return nullptr;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
private:
    Node *pre, *head;
    void dfs(Node* cur) {
        if(cur == nullptr) return;
        dfs(cur->left);
        if(pre != nullptr) pre->right = cur;
        else head = cur;
        cur->left = pre;
        pre = cur;
        dfs(cur->right);
    }
};

统计信息

通过次数	提交次数	AC比率
113355	173184	65.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言