原文链接: https://leetcode-cn.com/problems/O4NDxx

中文题目

给定一个二维矩阵 matrix，以下类型的多个请求：

• 计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

• NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
• int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

 

示例 1：

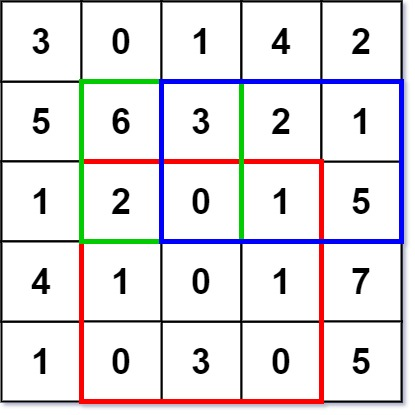
输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]

解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

 

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• -105 <= matrix[i][j] <= 105
• 0 <= row1 <= row2 < m
• 0 <= col1 <= col2 < n
• 最多调用 104 次 sumRegion 方法

 

注意：本题与主站 304 题相同： https://leetcode-cn.com/problems/range-sum-query-2d-immutable/

通过代码

高赞题解

解题思路

• 对于一个二维矩阵，可能由于输入不同的坐标而反复求不同子矩阵的数字之和，所以需要尽可能快的实现子矩阵的数字求和

• 用前缀和的方式可快速求子矩阵的数字和

• 为了代码实现上方便，特意在最左边一列，最上边一列空出来
  

• 先根据原矩阵，求出前缀和矩阵，然后通过观察得知公式
  sum[row2 + 1][col2 + 1] - sum[row1][col2 + 1] - sum[row2 + 1][col1] + sum[row1][col1]

• 举例来说上图红框中的和，就是上面第三图当中黄色圈出来的数字28-8-9+3 = 14

代码

/**
 * @param {number[][]} matrix
 */
let sum;
var NumMatrix = function(matrix) {
  // 非空判断处理
  if (matrix == null || !matrix.length || !matrix[0].length) {
    return;
  }
  // 初始化前缀和数组
  // 如果输入矩阵的行数和列数分别是m和n，那么sum辅助矩阵的行数和列数分别是m+1和n+1，只是为了简化代码逻辑
  sum = new Array(matrix.length + 1)
    .fill(0)
    .map(() => new Array(matrix[0].length + 1).fill(0));
  for (let i = 0; i < matrix.length; i++) {
    let rowSum = 0;
    for (let j = 0; j < matrix[0].length; j++) {
      rowSum += matrix[i][j] - 0;
      sum[i + 1][j + 1] = sum[i][j + 1] + rowSum;
    }
  }
};

/** 
 * @param {number} row1 
 * @param {number} col1 
 * @param {number} row2 
 * @param {number} col2
 * @return {number}
 */
NumMatrix.prototype.sumRegion = function(row1, col1, row2, col2) {
  // 公式sum[r2][c2] + sum[r1 - 1][c2] - sum[r2][c1 - 1] + sum[r1 - 1][c1 - 1];
  // 来求解左上角坐标(r1,c1)右下角(r2,c2)的子矩阵的数字之和，
  // 由于坐标r1或c1有可能等于0，因此r1-1或c1-1可能是负数，
  // 所以在辅助矩阵的最上面增加一行，最左边增加一列，这样就不必担心出现数组下标-1的的情形
  return (
    sum[row2 + 1][col2 + 1] -
    sum[row1][col2 + 1] -
    sum[row2 + 1][col1] +
    sum[row1][col1]
  );
};

统计信息

通过次数	提交次数	AC比率
5354	8139	65.8%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言