原文链接: https://leetcode-cn.com/problems/pOCWxh

中文题目

给定一个二叉树 根节点 root ，树的每个节点的值要么是 0，要么是 1。请剪除该二叉树中所有节点的值为 0 的子树。

节点 node 的子树为 node 本身，以及所有 node 的后代。

 

示例 1:

输入: [1,null,0,0,1]
输出: [1,null,0,null,1] 
解释: 
只有红色节点满足条件“所有不包含 1 的子树”。
右图为返回的答案。

示例 2:

输入: [1,0,1,0,0,0,1]
输出: [1,null,1,null,1]
解释: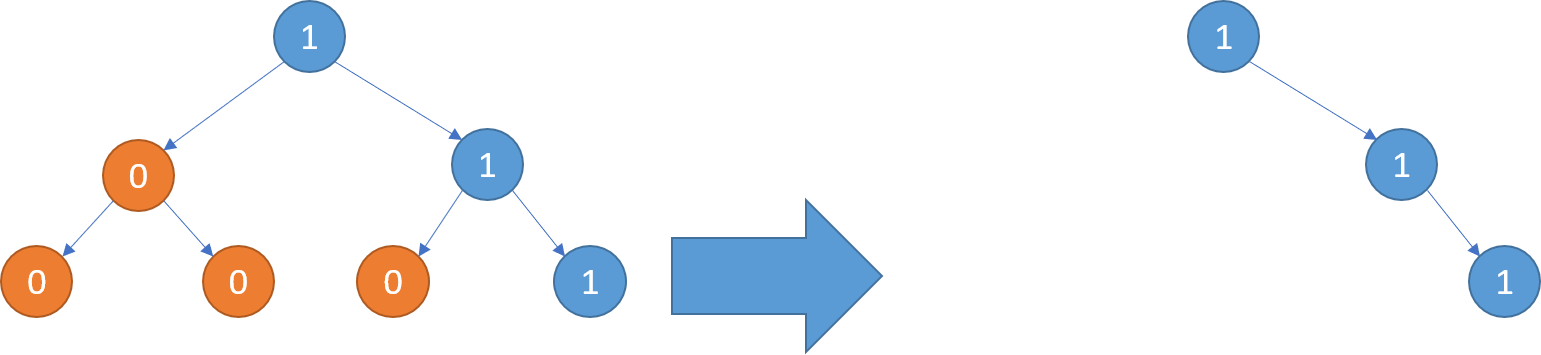 

示例 3:

输入: [1,1,0,1,1,0,1,0]
输出: [1,1,0,1,1,null,1]
解释: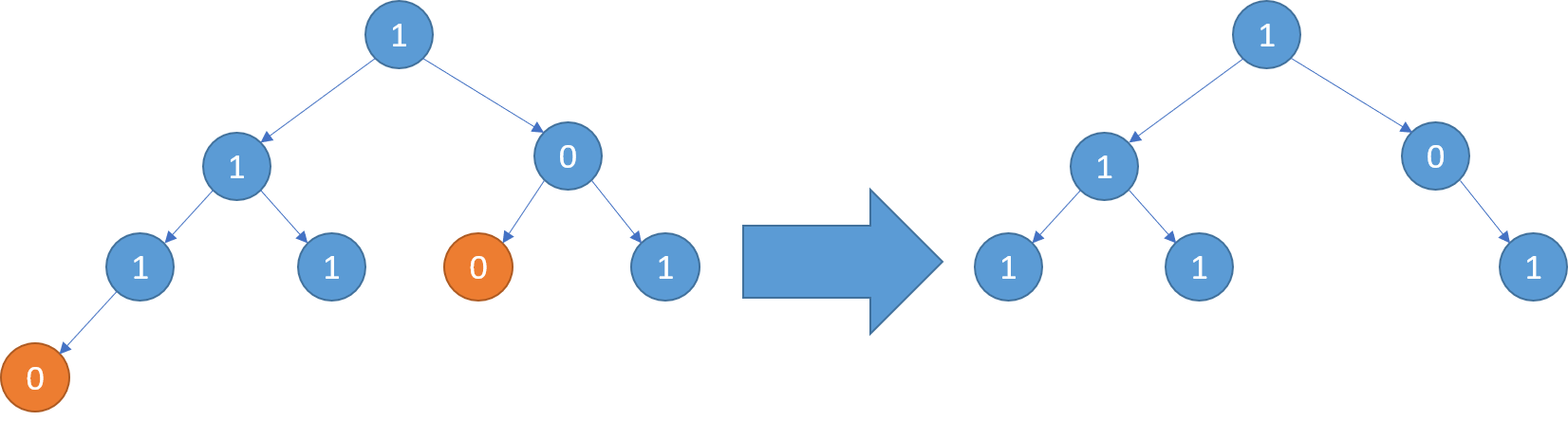 

 

提示:

• 二叉树的节点个数的范围是 [1,200]
• 二叉树节点的值只会是 0 或 1

 

注意：本题与主站 814 题相同：https://leetcode-cn.com/problems/binary-tree-pruning/

通过代码

高赞题解

后序遍历

二叉树结构是具有递归性质的，即每一个子树的本身也是一棵二叉树。其结构如下图：

若把全为 0 的二叉树称为零树，那么判断一棵树为零树的的规则是，左右子树都为零树或者空指针且根节点的值为 0。因为二叉树结构的递归性质，所以可以用同样的规则判断左右子树是否为零树。在使用递归函数时，让根节点的左右指针指向左右子树递归函数的返回值，当该二叉树判断为零树（左右指针指向空指针且其根节点的值为 0），则返回空指针，反之则返回根节点。

整个递归函数的过程都是先处理左右孩子节点再处理当前节点，这是后序遍历的一种变型。

代码如下

class Solution {
public:
    TreeNode* pruneTree(TreeNode* root) {
        if (root == nullptr) {
            return nullptr;
        }
        TreeNode* left = pruneTree(root->left);
        TreeNode* right = pruneTree(root->right);
        if (root->val == 0 && left == nullptr && right == nullptr) {
            return nullptr;
        }
        root->left = left;
        root->right = right;
        return root;
    }
};

这道题其实已经完了，但是再介绍下二叉树深度搜索的三种遍历方式：先序遍历、中序遍历和后序遍历的递归和迭代两种方式的实现。因为直接看代码比较高效，所以不做过多解释直接上代码。

先序遍历

1. 递归

void preorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    node.push_back(root->val);
    preorderTra(root->left, nodes);
    preorderTra(root->right, nodes);
}

2. 迭代

void preorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            nodes.push_back(cur->val);
            sta.push(cur);
            cur = cur->left;
        }

        cur = sta.top();
        sta.pop();
        cur = cur->right;
    }
}

中序遍历

1. 递归

void inorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    inorderTra(root->left, nodes);
    node.push_back(root->val);
    inorderTra(root->right, nodes);
}

2. 迭代

void inorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            sta.push(cur);
            cur = cur->left;
        }

        cur = sta.top();
        sta.pop();
        nodes.push_back(cur->val);
        cur = cur->right;
    }
}

后序遍历

1. 递归

void postorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    postorderTra(root->left, nodes);
    postorderTra(root->right, nodes);
    node.push_back(root->val);
}

2. 迭代

void postorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    TreeNode* prev = nullptr;
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            sta.push(cur);
            cur = cur->left;
        }

        cur = sta.top();
        if (cur->right != nullptr && cur->right != prev) {
            cur = cur->right;
        }
        else {
            sta.pop();
            nodes.push_back(cur->val);
            prev = cur;
            cur = nullptr;
        }   
    }
}

统计信息

通过次数	提交次数	AC比率
4373	6384	68.5%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言