原文链接: https://leetcode-cn.com/problems/7LpjUW

中文题目

树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

 

示例 1：

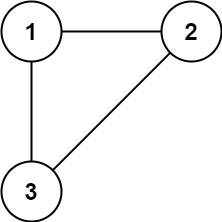
输入: edges = [[1,2],[1,3],[2,3]]
输出: [2,3]

示例 2：

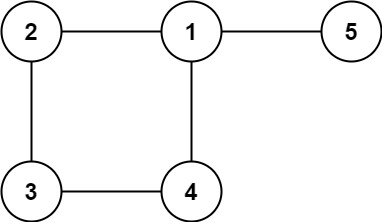
输入: edges = [[1,2],[2,3],[3,4],[1,4],[1,5]]
输出: [1,4]

 

提示:

• n == edges.length
• 3 <= n <= 1000
• edges[i].length == 2
• 1 <= ai < bi <= edges.length
• ai != bi
• edges 中无重复元素
• 给定的图是连通的 

 

注意：本题与主站 684 题相同： https://leetcode-cn.com/problems/redundant-connection/

通过代码

高赞题解

并查集

如果把树看做图，那么树就是不存在环的图，一棵有 n 个节点的树有 n - 1 条边。在树上添加一条多余的边就会存在环。需要明确形成环的原因，以题中 edges = [[1,2],[1,3],[2,3]] 为例，最开始 3 个节点都是离散的，任何两个节点之间都不存在边连接，也就是说是 3 个子图，如图(a)所示。先在图内添加一条边 [1,2]，于是节点 1 和节点 2 所在子图连在一块形成新的子图，如图(b)所示。接下来添加边 [1,3] ,于是节点 1 和节点 3 所在子图连在一块形成新的子图，如图(c)所示。最后添加边 [2,3]，因为节点 2 和节点 3 原本就属于同一个子图，此时再相连就会形成环。

通过以上分析可以发现，在添加一条边时若两个节点原本就属于同一个子图就会形成环。因此，为了找到多余的边需要解决两个问题，其一是如何判断两个子图是否属于同一个子图，其二是如何合并两个子图。并查集可以很好得解决这两个问题，完整代码如下，若节点数为 n，算法的时间复杂度为 O(n)。

class Solution {
private:
    int findFather(vector<int>& fa, int node) {
        if (fa[node] == node) {
            return node;
        }
        fa[node] = findFather(fa, fa[node]);
        return fa[node];
    }

public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> fa(edges.size() + 1);
        for (int i = 1; i < edges.size(); ++i) {
            fa[i] = i;
        }

        int ret = -1;
        for (int i = 0; i < edges.size(); ++i) {
            int father1 = findFather(fa, edges[i][0]);
            int father2 = findFather(fa, edges[i][1]);
            if (father1 != father2) {
                fa[father2] = father1;
            }
            else {
                ret = i;
            }
        }
        
        if (ret == -1) {
            return {};
        }
        return edges[ret];
    }
};

进一步分析可以发现，因为 edges 的长度为 n 且不存在重复边，而一棵有 n 个节点的树只会有 n - 1 条边，并且 edges 确定的图肯定由一根树添加一条多余的边组成的，所以在使用并查集查询时，找到的多余的这条边一定就是 “如果有多个答案，则返回数组 edges 中最后出现的边 ”。缩减后的代码如下。

class Solution {
private:
    int findFather(vector<int>& fa, int node) {
        if (fa[node] == node) {
            return node;
        }
        fa[node] = findFather(fa, fa[node]);
        return fa[node];
    }

public:
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
        vector<int> fa(edges.size() + 1);
        for (int i = 1; i < edges.size(); ++i) {
            fa[i] = i;
        }

        for (int i = 0; i < edges.size(); ++i) {
            int father1 = findFather(fa, edges[i][0]);
            int father2 = findFather(fa, edges[i][1]);
            if (father1 != father2) {
                fa[father2] = father1;
            }
            else {
                return edges[i];
            }
        }

        return {};
    }
};

统计信息

通过次数	提交次数	AC比率
1483	2092	70.9%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言