原文链接: https://leetcode-cn.com/problems/05ZEDJ

英文原文

中文题目

「力扣挑战赛」有 `n` 个比赛场馆（场馆编号从 `0` 开始），场馆之间的通道分布情况记录于二维数组 `edges` 中，`edges[i]= [x, y]` 表示第 `i` 条通道连接场馆 `x` 和场馆 `y`(即两个场馆相邻)。初始每个场馆中都有一定人数的志愿者（不同场馆人数可能不同），后续 `m` 天每天均会根据赛事热度进行志愿者人数调配。调配方案分为如下三种： 1. 将编号为 `idx` 的场馆内的志愿者人数减半； 2. 将编号为 `idx` 的场馆相邻的场馆的志愿者人数都加上编号为 `idx` 的场馆的志愿者人数； 3. 将编号为 `idx` 的场馆相邻的场馆的志愿者人数都减去编号为 `idx` 的场馆的志愿者人数。

所有的调配信息记录于数组 plans 中，plans[i] = [num,idx] 表示第 i 天对编号 idx 的场馆执行了第 num 种调配方案。
在比赛结束后对调配方案进行复盘时，不慎将第 0 个场馆的最终志愿者人数丢失，只保留了初始所有场馆的志愿者总人数 totalNum ，以及记录了第 1 ~ n-1 个场馆的最终志愿者人数的一维数组 finalCnt。请你根据现有的信息求出初始每个场馆的志愿者人数，并按场馆编号顺序返回志愿者人数列表。

注意：

• 测试数据保证当某场馆进行第一种调配时，该场馆的志愿者人数一定为偶数；
• 测试数据保证当某场馆进行第三种调配时，该场馆的相邻场馆志愿者人数不为负数；
• 测试数据保证比赛开始时每个场馆的志愿者人数都不超过 10^9；
• 测试数据保证给定的场馆间的道路分布情况中不会出现自环、重边的情况。

示例 1：

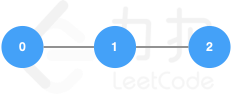
输入：
finalCnt = [1,16], totalNum = 21, edges = [[0,1],[1,2]], plans = [[2,1],[1,0],[3,0]]

输出：[5,7,9]

解释：
{:height=200}

示例 2 ：

输入：
finalCnt = [4,13,4,3,8], totalNum = 54, edges = [[0,3],[1,3],[4,3],[2,3],[2,5]], plans = [[1,1],[3,3],[2,5],[1,0]]

输出：[10,16,9,4,7,8]

提示：

• 2 <= n <= 5*10^4
• 1 <= edges.length <= min((n * (n - 1)) / 2, 5*10^4)
• 0 <= edges[i][0], edges[i][1] < n
• 1 <= plans.length <= 10
• 1 <= plans[i][0] <=3
• 0 <= plans[i][1] < n
• finalCnt.length = n-1
• 0 <= finalCnt[i] < 10^9
• 0 <= totalNum < 5*10^13

通过代码

高赞题解

方法：模拟

思路及算法
由于倍增和加减操作都是线性，考虑对线性操作的做线性拆分，将以 val = k * x + b 的形式表达出来， x 即为场馆 0 在所有操作后的人数
引入两个数组：

1. oriParam 数组表示每个位置 i 的系数 k
2. oriCnt 数组表示每个位置 i 的常数 b

此时每个位置 i 的值 val 就等于 oriParam[i] * x + oriCnt[i]
显而易见，
初始状态：

• oriCnt[i+1] = finalCnt[i]
• oriParam[0] = 1

用 HashMap 保存相邻场馆，之后模拟 plans 的操作。
以示例一为例，两个数组的变化情况如下：

得到初始状态表示数组的每个数后，求和就能得到 totalNum，此时就可以反解出 x
最后 将常数数组 oriCnt 加上 k * x 即为初始值

代码

class Solution {

  public int[] volunteerDeployment(int[] finalCnt, long totalNum, int[][] edges, int[][] plans) {
    int n = finalCnt.length + 1, m = plans.length;
    int[] oriParam = new int[n];
    int[] oriCnt = new int[n];
    oriParam[0] = 1;
    for (int i = 0; i < n - 1; i++) {
      oriCnt[i + 1] = finalCnt[i];
    }
    HashMap<Integer, List<Integer>> related = new HashMap<>();
    for (int[] e : edges) {
      //保存相邻场馆
      addRelations(e[0], e[1], related);
      addRelations(e[1], e[0], related);
    }
    for (int i = m - 1; i >= 0; i--) {
      int idx = plans[i][1];
      int num = plans[i][0];
      //模拟 plans 的操作
      operate(num, idx, oriParam, related);
      operate(num, idx, oriCnt, related);
    }
    //汇总k0,k1,k2...及 y - b0 - b1 - ...
    int param = 0;
    for (int i = 0; i < n; i++) {
      totalNum -= oriCnt[i];
      param += oriParam[i];
    }
    //求解x
    int x = (int) (totalNum / param);
    //将常数数组加上 k * x 即为初始值
    for (int i = 0; i < n ; i++) {
      oriCnt[i] += oriParam[i] * x;
    }
    return oriCnt;
  }

  private void operate(int num, int idx, int[] array, HashMap<Integer, List<Integer>> related) {
    if (num == 1) array[idx] *= 2;
    else {
      for (int r : related.getOrDefault(idx, new ArrayList<>())) {
        if (num == 2) array[r] -= array[idx];
        else array[r] += array[idx];
      }
    }
  }

  private void addRelations(int x, int y, HashMap<Integer, List<Integer>> related) {
    List<Integer> relations = related.getOrDefault(x, new ArrayList<>());
    relations.add(y);
    related.put(x, relations);
  }

结语
如果对您有帮助，欢迎点赞、收藏、关注 沪里户外，让更多的小伙伴看到，祝大家offer多多，AC多多！

统计信息

通过次数	提交次数	AC比率
953	2482	38.4%

提交历史

提交时间	提交结果	执行时间	内存消耗	语言